Globularにおける定理と証明とは何でしょうか? 実は、この問には明確な答はありません。強いて言えば、あなたが定理だと感じたものは定理だろうし、あなたが証明だと思いたいものは証明でしょう。
曖昧過ぎますか? -- しかしでは、Globularの外の世界で定理や証明が何であるか、カッチリと決まっているのでしょうか。特定の枠組み、例えば一階述語論理において定理や証明を定義することはできるでしょうが、それこそが定理/証明だと言い切れるでしょうか。
定理や証明について、もう一度考え直してもいいかも知れません -- Globularは、我々が常識だと思っているモノも再考する余地があることを教えてくれます。
内容:
- 構築可能性判断
- ワークスペースとリーズニング
- リーズニング記述言語とリーズニング・スクリプト
- 余談:n次元言語の未来
- 非公式自家製リーズニング記述言語
- Theoremコマンド
- 等式的推論
- テキスト言語との対応
構築可能性判断
通常の論理の知識*1は仮定します。A1, ..., An, Bが論理式だとして、A1, ..., Anを仮定してBを形式的に証明できることを次のように書きます。
- A1, ..., An |- B
これはメタな主張なので判断(judgement)と呼びます。「証明が可能である」と主張しているので、詳しく言えば証明可能性判断(provability judgement)です。ちなみに型理論では、型判断(typing judgement)なんて判断が出てきます。
[追記 date="201-09-15"]
以下で、構築可能性判断という概念を導入し、その記号に'|-'を使っています。証明可能性判断と同じ記号です。証明可能性も構築可能性も似たようなものだから、という理由ですが、同じではないので、記号を変えるべきだと思います。とりあえずはそのままにしておきますが、修正するかも知れません。
構築可能性と証明可能性は密接に関連しますが、この記事ではその関連の分析がされていません。この点も、いずれ(別記事で)詳述したいと思います。
[/追記]
Globularでは、型、項、論理式などの区別はありません。ダイアグラム(図式)があるだけです。それでも、判断(メタな主張)には意味があります。C1, ..., Cn, D がダイアグラムだとして、C1, ..., Cn が既に存在するとき、それらをもとにしてDが構築可能なことを、次のように書きましょう。
- C1, ..., Cn |- D
この判断を構築可能性判断(buildability judgement)と呼ぶことにします。通常の証明可能性判断も、証明(と呼ばれるナニモノカ)の構築可能性を主張しているので同じことです。以下で単に「判断」といった場合、構築可能性判断を意味します。
特にGlobularというシステムのなかで構築可能であることを強調したいなら、その旨を添えます。
- C1, ..., Cn |-Globular D
Globularの場合、'|-'の左側に出てくるダイアグラムはすべてセルである必要があります。セル(cell)とはダイアグラムの一種ですが、次の条件を満たすものです。
- セルの条件: ノード(点、ドット)をただ1つだけ含む。
0次元のセル=0次元のダイアグラム=一点 です。ノードは色付きの円板としてビジュアライズされるので、ダイアグラムがセルかどうかは目視で判断できます。以下の2つのダイアグラムはセルではありません。1番目はノードが2つある1次元ダイアグラム、2番目はノードが1個もない2次元ダイアグラムです。
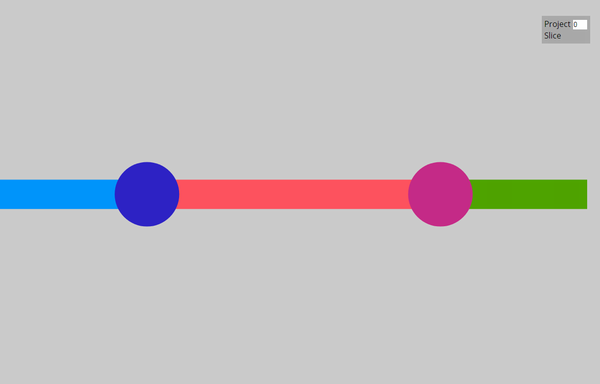

ワークスペースとリーズニング
構築可能性判断のメタ記号'|-'の左側をセルの集合だと解釈しましょう。すると、判断を次のように書けます。
- {C1, ..., Cn} |- D
Globularでは、セルの集合を指標(signature)と呼び、Σで表すのが習慣です。指標Σを使えば:
- Σ |- D
指標Σは、GUIのセルパレットに対応します。判断 Σ |- D は、セルパレット(の状態)がΣで、ビューペインにダイアグラムDが置かれている(出来ている)状態を表現しています。
Σはセル(単一ノードのダイアグラム)の集合だと言いました。しかし、勝手にセルを集めてきた集合ではダメです。セルの集合が指標であるためには、幾つかの条件を満たす必要があります。いま、その条件を述べませんが、セルの集合Σが指標としての制約条件を満たすことを次の形で書きます。
- ||- Σ
'||-'もメタな記号で、「Σは指標である」と読めばいいでしょう。この形のメタな主張は、指標であるかどうかの判断なので、指標判断(signature judgement)と呼ぶことにします。
次の(メタな)表現は、「Σが指標であり、そのΣからダイアグラムDが構築可能である」ことを主張します。
- ||- Σ, Σ |- D
パレットと(ビューペインに見えている)ダイアグラムを一緒に考えたものがGlobularのワークスペースです。なので、次のように言えます。
- ワークスペースは、指標判断と構築可能性判断のソフトウェア的・物理的表現である。
- 指標判断と構築可能性判断は、ワークスペースのメタ論理的表現である。
判断 ||- Σ, Σ |- D が正しいことを示すには、指標Σのもとで実際にダイアグラムDを作るしかありません。ワークスペース(Σ, D)を作る、と言っても同じです。判断が正しいことを示す(=ワークスペースを作る)行為をリーズニング(reasoning)と呼びます。
リーズニングは我々人間が遂行する行為です。それに対して指標(セルパレット)ΣやダイアグラムDはソフトウェアが保持するデータです。人間の行為とソフトウェアが持つデータはまったく別物ですが、多くの場合に混同されています。Globularでは、リーズニングを人間が目視と手動で行うしかないので、このような混同は起きにくいですね。
リーズニング記述言語とリーズニング・スクリプト
通常の証明支援形の場合、リーズニングを記述する言語を持っています。タクティク言語(tactic language)と呼ばれます。リーズニングの基本操作をタクティクと呼ぶ習慣があるのです。タクティク言語で書かれたソースコードは証明スクリプト(proof script)といいます*2。
証明スクリプト(タクティク言語によるコード)とは別に、証明オブジェクトと呼ばれるデータがあります。Coqの場合は、pCic形式ラムダ項が証明オブジェクトです。Isabelleの証明オブジェクトはユーザーからは見えない内部的データです*3。
証明支援系の説明では、「人間が行う行為であるリーズニング」、「リーズニング過程を記述する証明スクリプト」、「リーズニングの結果としてソフトウェア内部に作られる証明オブジェクト」が区別されてなくて僕はイライラします。ここでは、「証明」を証明オブジェクトの意味で使うので、「タクティク言語→リーズニング記述言語」「証明スクリプト→リーズニング・スクリプト」という言い換えをします。
現状の証明系の問題点は:
- リーズニング・スクリプトが難読過ぎて読めない。
- 証明オブジェクトはさらに難読か、または隠蔽されている。
Isabelleはこの問題を、今までの指令(インストラクション)言語に代えて宣言的構造化言語を導入して解決しようとしています。
さてGlobularですが、ソフトウェアの操作は100%GUIなので、リーズニング記述言語を持ってません。当然ながらリーズニング・スクリプトはありません。存在するのは証明オブジェクトだけです。Globular内のオブジェクト(モノ、thing)とはダイアグラムなので、証明オブジェクト=証明ダイアグラムです。
与えられたダイアグラムを「証明オブジェクト」とみなすかどうかは解釈の問題で、Globular自身に「ダイアグラムが証明かそうでないか」を決めるメカニズムは一切ありません。とりあえず、目の前のダイアグラムを“証明オブジェクトとみなす”ことにして、証明支援系としての問題点・懸念点は:
- 証明オブジェクトは可読か? 作者以外(ときに作者でさえ)読めないならコミュニケーションに使えない。
- リーズニング・スクリプトが存在しないが、それで大丈夫なのか?
この問に一度に答えることは難しいし、答には主観(立場や主義)が入ります。この問を頭の片隅に置いて、答を探していきたいと思います。今の僕の主観から大雑把に言えば、絵図言語(pictorial/graphical/diagrammatic lauguage)が普及して、ソフトウェアのビューイング機能がもっと充実すれば*4、証明オブジェクト=証明ダイアグラムは十分に可読で、リーズニング・スクリプトは原則的に不要だと思います。ただし、リーズニング・スクリプトがあれば便利なのは確かなので、実装を希望はします。
Globularにとっての困難の主たる要因は文化的なものでしょう。つまり、絵図言語が普及してないことです。ダイアグラムが“謎の絵”にすぎないなら、「可読か?」という問はナンセンスです。
余談:n次元言語の未来
「記法バイアスと記法独立な把握: 順序随伴を例として」でマンガの例を出しました。マンガは、文字と絵を融合させて、独自の語彙・文法・記法を発展させて、紙面の2次元性を活用したコミュニケーション手段となりました。
コミュニケーション技術の受容と活用の点からは、エンタテインメントの世界は先進してます。最近だと、VRヘッドマウントディスプレイを利用したVRゲームがあります。視覚・聴覚以外に触覚もシミュレートできるとさらにリアリティが増すでしょう。
3次元ディスプレイ技術をGlobularで利用できるとすると、スチル(静止像、非アニメーション)ビューでも3次元ダイアグラムを直接表示できます。時間方向を使ったムービービューなら4次元ダイアグラムを閲覧(むしろ体験)できます。5次元ダイアグラムはスライシング(紙芝居)ビューになりますが、複数の“世界線”のトランジション・シーケンスとして体験できます。
次元が高くなると情報量が極端に増加するので、視覚的な色・透過度だけでなく聴覚(音)と触覚も利用できたほうが望ましいでしょう。こうなると、文字という有限個の記号を1次元に並べただけのテキスト媒体とは比べものにならない膨大な情報を受け取ることになります。
視覚・聴覚・触覚を総動員した4次元・5次元の言語(語彙・文法・記法)に載せて情報コンテンツを伝達できたとしたら、これはコミュニケーションの革命と呼べるでしょう。
僕が、n次元の圏/n次元の絵図とそれを扱うソフトウェアに興味を持つのは、n次元言語コミュニケーションがエンタテインメント・コンテンツだけでなくSTEM(Science, Technology/Engineering, and Mathematics)コンテンツにも使われる(遠い)未来を信じてるからです。そのような世界ではSTEM教育は何倍・何十倍にも加速されると期待できます。
非公式自家製リーズニング記述言語
Globularにリーズニング記述言語はないし、原則的に不要だと言いました。しかし、Globular自体の機能もGlobularの利用環境も不十分である現時点では、リーズニング記述言語があったほうが便利です。そこで、前回記事「Globularの使い方 (2): サンプル・ワークスペース」で私製リーズニング記述言語を定義しました。
若干の拡張と手直しをします。
ダイアグラムを値として代入できる変数概念を導入します。システムの予約変数としてitとotherがあるとします。itには、直前のオペレーションの結果が代入されます。結果とはダイアグラムですが、ダイアグラムを新規生成するオペレーションには次があります。
- New
- SourceとTargetのペア
- Theorem
作られた新規セルがitに入ります。Theoremでは2つの新規セルが作られるので、一番目をitに代入して、二番目をotherに代入するとします。Makeオペレーションの第1引数にはitかotherを明示するようにします。
ユーザー定義変数も使えるとしますが、これはいずれ(今回ではない)実際の使用例と共に説明します。
Theoremコマンド
GlobularのTheoremコマンドの説明をします。名前からいって「定理」と何か関係しそうです。ですが、あまり期待や先入観を持たないほうがいいです。我々が常識的に「定理」と思っている概念に関係はしますが、定理とは無関係な場面でもTheoremコマンドは使います。
Theoremコマンドを使うサンプルとして次のワークスペースを準備しました。
このワークスペースと同じワークスペースを作る手順は次のとおりです。最初に状況設定:
- New; Make it A:0
- New; Make it B:0
- New; Make it C:0
- New; Make it D:0
- Select A; Source; Select B; Target; Make it f:1 A->B
- Select B; Source; Select C; Target; Make it g:1 B->C
- Select C; Source; Select D; Target; Make it j:1 C->D
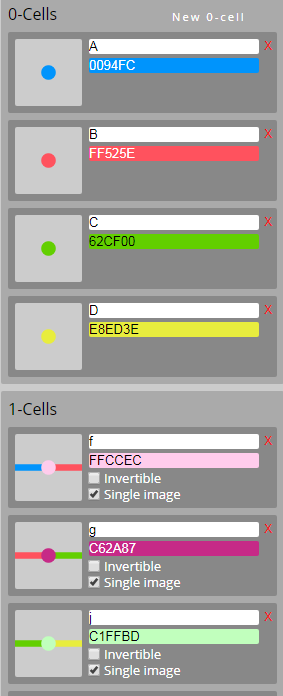
次に、Theoremコマンドを使って次のようにします。
- Select f; Attach g (1); Theorem; Make it h; Make other "h := f;g"
Attach g のときの選択肢は1個しか出ませんが、マウスクリックは必要です。別な操作法として、fのビューのなかでBに対応する線の上でクリックするとBに対してgがアタッチされます。
問題のTheorem実行ですが、A→C という1次元セルが作られるので、それにhと名前を付けます。この場合、Theoremは定義に使われています。fとgを結合したf;gにhという名前を付けているのです。もう1個の2次元セルが定義内容を表現していて、h ⇒ f;g 、つまり「hとは、f;gのことだよ」と言っています。このセルには、h := f;g という説明的ラベルを付けました。

矩形の下の辺が h:A→C を表現していて、上の辺が f;g:A→C です。そして、矩形中央の青いノードが h ⇒ f;g : A→C を代表しています。なので、この2次元セルはhの定義と解釈できるのです。
同様にしてkを定義します。
- Select j; Theorem; Make it k; Make other "k := j"
新しく定義したkはjと同じものです。定義内容は k ⇒ j : C→D で、次のようになります。下から中央までの縦線がk、中央から上までの縦線がjで、中央の薄茶色ノードが定義自体です。

等式的推論
2つの定義 h := f;g と k := j は、等式とみなすことができます。この等式の左辺どおし、右辺どおしを結合すると、次の等式が得られます。
- h;k = f;g;j
これには、2つの仮定から結論を得るリーズニングが必要です。リーズニングの仕様(前提と目標)は:
- 仮定1 h = f;g
- 仮定2 k = j
- 結論 h;k = f;g;j
結論のダイアグラムを構成するだけなら次のようにできます。
- Select h; Attach k (1); Source
- Select f; Attach g (1); Attach j (1); Target

ただし、このダイアグラム(h;k = f;g;j を意味する)を手で直接作っても意味がなく、2つの仮定を使って作り出す(導き出す)過程、つまりリーズニングをダイアグラムにエンコードする必要があります。次のようにします。
- Select h; Attach k (1);
- Idenity
- Attach "k := j" (1)
- Attach "h := f;g" (1);
この段階で、ビューペインのダイアグラムは次のようになっています。

この図は h;k = f;g;j の証明と呼んでよいものです。下から上に順に見ていくと、下の辺は h;k を意味しています。薄茶色のノードは仮定の1つ k = j で、この等式を適用した後(すぐ上の領域)では h;j になっています。もう1つの仮定 h = f;g (青いノード)を通りぬけると f;g;j なので、全体として結論である h;k = f;g;j を意味しています。
この状態でTheoremコマンドを実行すると、定理のステートメント(結論)である2次元セルと、ステートメントと証明ダイアグラムを繋ぐ3次元セルが生成されます。
- Theorem
- Make it "Eq. h;k = f;g;j"
- Make other "Eq. and Proof"
- Select "Eq. and Proof"; SetView(Project=0, Slice=1)
テキスト言語との対応
うんと未来の子供たちが、ボブ・クックが言うように、幼稚園/小学校から絵図言語に親しむようになれば、テキストと絵の対応なんて誰も気にしなくなるでしょう。しかし、今の時代の我々は、ほぼテキスト言語でコミュニケーションしているので、翻訳が必要です。
今回使った指標(セルパレット)の内訳は:
- 0次元セルが4個
- 1次元セルが5個
- 2次元セルが3個
- 3次元セルが1個
それぞれのセルは(一例として)次のように解釈できます。
- 0次元セル A:0, B:0, C:0, D:0 は、基本型である。
- 1次元セル f:1 A→B, g:1 B→C, j:1 C→D は、基本関数である。
- 1次元セル h:1 A→C, k:1 C→D は、ユーザー定義関数である。
- 2次元セル "h := f;g" は、hを定義する等式的命題である。"k := j" も同じく等式的命題である。ターゲットダイアグラム(上の辺の1次元ダイアグラム)は関数を組み合わせた項である。
- 2次元セル "Eq. h;k = f;g;j" は、定理のステートメント(結論)である等式的命題である。
- 3次元セル "Eq. and Proof" は、定理のステートメントと証明をパッケージしたものである。このセルのターゲットダイアグラムは証明ダイアグラム(ダイアグラムとしての証明オブジェクト)である。
このような簡単な例の翻訳を通じて、テキスト言語と絵図言語がまったくかけ離れたものではないことが実感できるようになるでしょう。