アレンジメント計算 7： AlmostSurelyEqual - 檜山正幸のキマイラ飼育記 (はてなBlog)

「アレンジメント計算 5：リンク積」において、リンク積の定義の難しさについて述べました：

難しさの要因は、マルコフ圏の条件化可能性公理にあります。条件化可能性公理を仮定すれば、任意の二部アレンジメントにその条件化（の結果）である射を対応付けることができます。が、この対応は一意に決まらないのです。この「条件化の不定性」がいたる所で顔を出します。
「条件化の不定性」をうまく扱える枠組みを作らないと、リンク積もうまく扱えないのです。

今まで「条件化の不定性」の問題を正面から議論することはなかったので、僕の説明には靄〈もや〉がかかったような不明瞭な感じが付きまとっていたかも知れません。早めに対処（って、既に第7回だけど）しないと、禍根を残すであろう、と。そういうわけで今回と引き続く回で、靄〈もや〉を晴らすことを試みます。「条件化の不定性」をうまく扱える枠組みを作りましょう。この話はね、ちょっと難しいし、なにより“めんどくせー！”んだよなー。めんどくさいけど、避けないで行きます。

この記事の本文内で正規表現（「アレンジメント計算 6：用語・記法の整理 // 正規表現」参照）を使っています。

内容：

事例に関して
参考文献と用語
マルコフ圏のAlmostSurelyEqual
マルコフテンソルの圏での具体的ASE
一般ASEと二段ASE
おわりに

シリーズ第1回兼リンクハブ：

アレンジメント計算 1：確率グラフィカルモデル

事例に関して

めんどくさい議論をするのに、抽象的なセッティングだけだと辛いですから、具体例を添えることにします。具体的なセッティングは、「アレンジメント計算 2：簡単な実例と注意事項 // 今回のセッティング」で述べたセッティングをそのまま使います。

この事例〈具体的なセッティング〉に関する言葉や記号をここでちょっと追加しておきます。有限集合と可算無限集合を一緒にして単に可算集合〈countable set〉と呼びます。対象を可算集合に制限したSetの充満部分圏を CountblSet とします。有限集合の圏は FinSet です。圏として次の包含関係があります。

FinSet ⊆ CountblSet ⊆ Set

任意の集合を離散可測空間として可測空間の圏に埋め込む関手 Set → Meas を考えます。この関手の像圏（離散可測空間の圏）とSetを同一視しましょう（それがいいとは思ってないけど）。この同一視のもとでは：

FinSet ⊆ CountblSet ⊆ Set ⊆ Meas

Set上の形式的凸結合モナドは、ディラック測度の和である測度による“ジリィ・スタイルのモナド”と考えることができます。したがって、形式的凸結合モナドのクライスリ圏はジリィ・スタイルの具体的確率圏〈concrete stochastic category〉です。対象を可算集合に制限した圏が我々が事例に使うマルコフ圏です。この事例の圏は、CountblDiscStoc と命名するのが自然でしょう、FinDiscStoc, DiscStoc を既に使っていますから。

FinDiscStoc ⊆ CountblDiscStoc ⊆ DiscStoc ⊆ Stoc

CountblDiscStoc の対象は、可算集合と同一視された離散可測空間で、射はマルコフ核です。F:A → B in CountblDiscStoc のとき、F:A×ΣB → [0, 1] in Set （'A' は可測空間と台集合でオーバーロード、ΣA = Pow(A)）なので、関数 f:A×B → [0, 1] in Set を次のように定義できます。

For x∈A, y∈B, f(x, y) := F(x, {y})

λy∈B.f(x, y) は、B上の確率測度 λT∈ΣB.F(x, T) の密度関数です。離散の場合は「密度関数」とはあまり言いませんが、定義上は間違いなく密度関数です。λ(x, y)∈A×B.f(x, y) は、「マルコフ核と確率密度関数」で述べたパラメータ付き確率密度関数〈確率密度核〉です。

マルコフ核の代わりにパラメータ付き確率密度関数〈確率密度核〉を射と考えても圏同型なマルコフ圏ができます。それが“可算集合をインデックス集合とするマルコフ行列”の圏 MarkovMat です。

CountblDiscStoc $\cong$ MarkovMat （圏同型）
|CountblDiscStoc| = |MarkovMat| = |CountblSet| （CountblSet ⊆ Meas とみなして）

圏同型な2つの圏は同一視可能ですが、ここでは区別しておきます。

「対称モノイド多圏（簡約版）」で述べた手順で StdPoly(MarkovMat) を作ると、それが“可算集合をインデックス集合とするマルコフテンソル”の圏 MarkovTens です。

MarkovTens = StdPoly(MarkovMat)
|MarkovTens| = List(|MarkovMat|) = List(|CountblSet|)

なお、「対称モノイド多圏（簡約版）」では、対称モノイド圏に対する PermStdPoly(C) という構成を紹介してますが、あれは不要でした。対称性があっても無くても StdPoly(C) で目的の簡約多圏が得られます（ゴメンナサイ）。

参考文献と用語

マルコフ圏に関して必要な知識は、次の2つの論文でカバーできます（内容に重複はあります）。

Title: A synthetic approach to Markov kernels, conditional independence and theorems on sufficient statistics
Author: Tobias Fritz
Submitted:19 Aug 2019 (v1), 31 May 2020 (v8)
Pages: 98p
URL: https://arxiv.org/abs/1908.07021

Title: Disintegration and Bayesian Inversion via String Diagrams
Authors: Kenta Cho, Bart Jacobs
Submitted: 29 Aug 2017 (v1), 8 Feb 2019 (v3)
Pages: 39p
URL: https://arxiv.org/abs/1709.00322

これらの論文を参照するとときは、[フリッツ p.77 13.10. Remark]、[長／ジェイコブス p.10] のような形式を使うことにします。

[フリッツ]と[長／ジェイコブス]では、使っている用語がだいぶ違います。表にまとめておきます。2つの論文を見比べるときは役に立つでしょう。

このブログ	フリッツ	長／ジェイコブス	備考
マルコフ圏	Markov category	affine CD-category	確率論の舞台
{マルコフ}?射	morphism	channel	マルコフ圏の射
マルコフ核	Markov kernel	channel	具体的な射
カップル	coupling	coupling	特殊な射
n脚アレンジメント	-	n-partite state	特殊な射
ASE	almost surely equal	almost equal	射のあいだの関係
確率測度(↑)	distribution	state	特殊な射
確率空間(↑)	probability space	-	構造
関連	measure-preserving morphism	state-preserving channel	構造のあいだの射
リンク積	≒conditional product	-	カップルに対する二項演算
条件化	conditioning	disintegration	圏上のオペレーター
-	disintegration	-	[フリッツ p.48]
制限	-	conditioning	[長／ジェイコブス p.28]
{ベイズ}?反転	Bayesian inversion	Bayesian inversion	圏上のオペレーター
条件化可能	has conditional distributions	admits disintegration	マルコフ圏の性質
反転可能	-	-	マルコフ圏の性質
一般条件化可能	has conditionals	-	マルコフ圏の性質
半デカルト	naturality of del	causal	準マルコフ圏の性質
順次因果的	causal	-	マルコフ圏の性質
等式強化可能	-	admits equality strengthening	マルコフ圏の性質

(↑)が付いている語（「確率測度」と「確率空間」）は、具体的な状況における用語ですが、このシリーズ記事では抽象的な状況でも使います。確率測度も確率空間も、マルコフ圏C内の ω:1 → A in C という射です。
「リンク積」と "conditional product" は同義ではなくて類義です。それで、'≒'が付いています。
"causal" の意味が[フリッツ]と[長／ジェイコブス]では違います。[長／ジェイコブス]の用法が多数派だと思います。[フリッツ]の "causal" は「順次因果的」としました。
"disintegration", "conditioning" の意味も[フリッツ]と[長／ジェイコブス]では違います。
その他、用語・記法に関する注意は「アレンジメント計算 6：用語・記法の整理」にあります。

マルコフ圏のAlmostSurelyEqual

確率に関わる話をややこしくしている元凶は、測度論に出てくる「ほとんど{いたる所 | 確実に}〈almost {everywhere | surely}〉ナントカ」ってヤツです。これは、測度論では、鬱陶しいけど必須の概念です。長／ジェイコブスは、ほとんど{確実に}?等しい〈almost {surely}? equal〉を、マルコフ圏において代数的に定義しました。長／ジェイコブスの定義により、測度論なしで測度論的概念を扱えるようになったのです。しかし、鬱陶しいことに変わりはありません*1。

「ほとんど{確実に}?等しい」をASEと略記します。頭文字で分かりにくいときは AlmostSurelyEqual とします。マルコフ圏の公理だけからASEを定義できます。以下にASEの定義を述べます。

Cをマルコフ圏だとして、f, g:A → B in C と p:1 → A in C に対して、f ～^p g を次のように定義します。

f ～^p g :⇔ p;Δ_A;(id_A $\otimes$ f) = p;Δ_A;(id_A $\otimes$ g) :1 → A $\otimes$ B in C

絵で描くなら次のようです。描画方向は上から下です。前節で紹介した論文達とは上下逆なので注意してください。

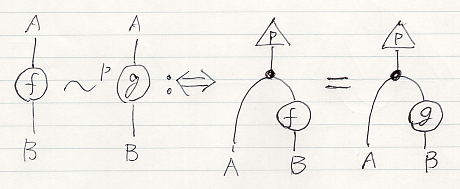
マルコフ圏C上のASEとは、この二項関係～^p を、すべての対象 A, B と p:1 → A in C に渡って寄せ集めた族です。対象 A, B に対する二項関係～^p （より正確に書けば～_A,B^p in C）は、ホムセット C(A, B) 上の同値関係になります。つまり、次が成立します。

For f:A → B in C
f ～^p f
For f, g:A → B in C
f ～^p g ⇒ g ～^p f
For f, g, h:A → B in C
f ～^p g かつ g ～^p ⇒ f ～^p h

これらは明らかでしょう。この二項関係～^p が我々の具体例でどうなっているかは次節で見ます。

マルコフテンソルの圏での具体的ASE

マルコフテンソルの圏MarkovTensにおいて、成分を使った計算をするときは、反図式順／反書字順記法が標準です。例えば、p;Δ_A;(id_A $\otimes$ f) は反図式順で (id_A $\otimes$ f) $\circ$ Δ_A $\circ$ p です。Δ_A の成分 Δ_A(x, (x', x'')) for x, x', x'' ∈A は反書字順で Δ_A(x', x''|x) for x, x', x'' ∈A になります。結合の順も引数並びの順も右から左です。ただし、モノイド積の順は左から右です。

マルコフ圏Cにおける f ～^p g の定義を再掲すると：

p;Δ_A;(id_A $\otimes$ f) = p;Δ_A;(id_A $\otimes$ g) :1 → A $\otimes$ B in C

ℓ := p;Δ_A;(id_A $\otimes$ f) = p;Δ_A;(id_A $\otimes$ g) :1 → A $\otimes$ B in MarkovTens と置いて、ℓの成分表示は次のように書けます。

$\:\:\:\: l(x, y\mid) \\ = \sum_{(x', x'')\in A\times A}(\, \mathrm{id}_A(x \mid x')f(y \mid x'') \sum_{t\in A}\Delta_A(x', x'' \mid t)p(t\mid)\,)$
$t = x' = x''$ のときだけ値が残り、他の場合はゼロなので、
$= \sum_{t \in A}(\, \mathrm{id}_A(x \mid t)f(y \mid t) p(t\mid)\,)$
さらに、 $t = x$ のときだけ値が残り、他の場合はゼロなので、
$= f(y \mid x) p(x\mid)$

同様に r := p;Δ_A;(id_A $\otimes$ g) in MarkovTens の成分表示を計算すると $r(x, y\mid) = g(y \mid x) p(x\mid)$ となります。これより、

$f \sim^p g \::\Leftrightarrow \forall (x, y)\in A\times A.(\, f(y \mid x) p(x\mid) = g(y \mid x) p(x\mid) \,)$

p(x|) = 0 であるときは f(y | x), g(y | x) の値に何の制約もなく、p(x|) ≠ 0 なら f(y | x) = g(y | x) が要求されます。つまり、

$f \sim^p g \::\Leftrightarrow \forall (x, y)\in A\times A.(\, p(x\mid) \neq 0 \Rightarrow f(y \mid x) = g(y \mid x) \,)$

この定義を見ると、f ～^p g とは、確率測度pがゼロでないところで f = g であることです。確率測度pがゼロであるところは無視されます。

測度論により、f ～^p g :A → B in Stoc が次と同値であることが示せるようです（[長／ジェイコブス p.17 Proposition 5.3]参照）。

$\forall S\in \Sigma A, T\in \Sigma B.\\ \left(\, {\displaystyle \int_{x\in S\subseteq A} f(T \mid x)p(dx) = \int_{x\in S\subseteq A} g(T \mid x)p(dx) }\,\right)$

一般ASEと二段ASE

前節で述べたASE f ～^p g :A → B in C は、マルコフ圏Cの確率測度 p:1 → A in C による同値関係でした。確率測度pごとに同値関係があります。

確率測度ではなくて、一般の射 w:W → A in C による同値関係も同様に定義できます。同じ記号～^w を使うことにして：

f ～^w g :⇔ w;Δ_A;(id_A $\otimes$ f) = w;Δ_A;(id_A $\otimes$ g) :W → A $\otimes$ B in C

絵で描くなら次のようです。

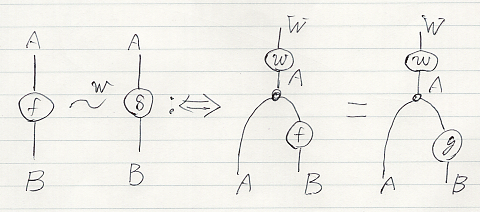
このように定義された～^w を一般ASE〈general ASE〉と呼ぶことにします。前節のASEは、一般ASEの特別な場合です。

具体的な確率圏Stocでの一般ASE f ～^w g in Stoc は次のように書けることが知られています（[フリッツ p.74 13.3. Example]参照）。

$\forall t \in W, S\in \Sigma A, T\in \Sigma B.\\ \left(\, {\displaystyle \int_{x\in S\subseteq A} f(T \mid x)w(dx\mid t) = \int_{x\in S\subseteq A} g(T \mid x)w(dx \mid t) }\,\right)$

f, g:A → B in C と p:1 → W, w:W → A in C があるとき、記号 $\approx$ ^p,w で表す同値関係を次のように定義します。

f $\approx$ ^p,w g :⇔ p;Δ_W;(id_W $\otimes$ (w;Δ_A;(id_A $\otimes$ f))) = p;Δ_W;(id_W $\otimes$ (w;Δ_A;(id_A $\otimes$ g))) :1 → W $\otimes$ (A $\otimes$ B) in C

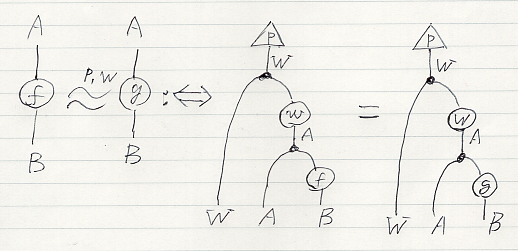
このように定義された $\approx$ ^p,w を二段ASE〈two-step ASE〉と呼ぶことにします。

さらに、二段ASEを一般化した一般二段ASE〈general two-step ASE〉は次のように定義します。v:V → W in C です。

f $\approx$ ^v,w g :⇔ v;Δ_W;(id_W $\otimes$ (w;Δ_A;(id_A $\otimes$ f))) = v;Δ_W;(id_W $\otimes$ (w;Δ_A;(id_A $\otimes$ g))) :V → W $\otimes$ (A $\otimes$ B)

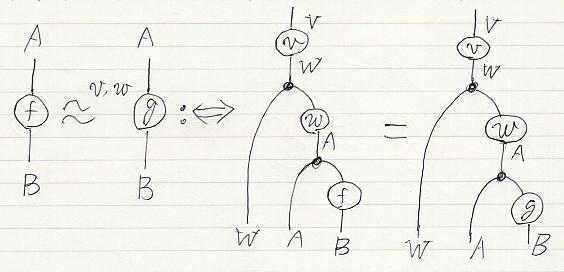
等号以外に、何種類ものASE〈almost surely equal〉が出てくるのは実に鬱陶しくめんどくさい話ですが、正確な議論をするには必要なことなので我慢しましょう。鬱陶しさがモヤモヤを晴らしてくれるのです。

おわりに

今回は、基本となるASEと、その一般化・変種である {{一般}?{二段}?}!ASE を定義しました。が、ここまでの説明だけでは、これらのASE達が圏の結合やモノイド積と整合するかどうか分からないし、ASE達の相互関係も不明です。これらのASE達の振る舞いを調べて、うまいこと組み合わせることにより、新しい圏や関手の構成に使いたいのです。それが次回以降の課題です。

*1:ほとんど等しいは、測度ゼロの集合を除いて等しいことです。可測だが測度はゼロである集合が厄介なわけですが、抽象化しても厄介さを解消することは出来ないようです。おそらく、測度ゼロ集合は夾雑物ではなくて本質的存在なのでしょう。