アレンジメント図は、幾つかのアレンジメントをワイヤーで繋いだ形をしています。ワイヤーで繋ぐとは何なのでしょうか? ワイヤーで繋ぐ操作に定式化を与えますが、この記事で完全な定義にまでは至っていません。
内容:
シリーズ第1回 兼 リンクハブ:
アレンジメントと因子グラフ
アレンジメントという概念を何のために導入したのか? その動機はシリーズの最初の記事「アレンジメント計算 1: 確率グラフィカルモデル」で紹介しました。確率グラフィカルモデルに出てくるグラフと、圏論で使用されるストリング図を相互に(ある程度は)翻訳したい、という要求が動機です。
確率グラフィカルモデルに出てくるグラフとしては、無向・有向の因子グラフを選び、それと(だいたい)対応するストリング図のクラス(ここでのクラス=図の集合)としてアレンジメント図/二部アレンジメント図のクラスを設定したのです。
単一のアレンジメントは、因子ノードを一つだけ持つ境界付き無向因子グラフに翻訳されます。以下のようです。図内で、因子ノードに接続する辺のうちの1本の根本に赤いマーク(バッテン)が付いています。これは番号1に対応する辺で、平面内で反時計回りに番号を付けることにします。
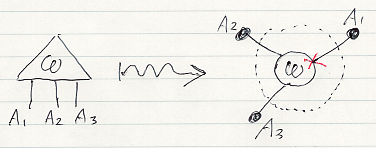
単一の二部アレンジメントは、因子ノードを一つだけ持つ境界付き有向因子グラフに翻訳されます。次のようです。
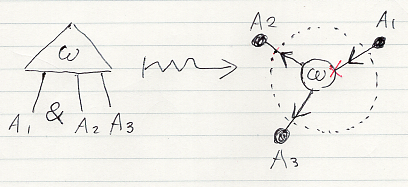
二部アレンジメントの左側の脚は入力辺になり、右側の脚は出力辺となり、それに応じた辺の向きが与えられます。
アレンジメント図にしろ因子グラフにしろ、ノードが一つだけでは面白くないですね。複数のノードを含むアレンジメント図/因子グラフでは、ワイヤー/辺でアレンジメントノード/因子ノードが接続されています。接続された3つのノードを持つアレンジメント図から無向因子グラフへの翻訳を示します。アレンジメントの二部化と因子グラフの有向化をすれば、二部アレンジメント図から有向因子グラフへの翻訳になります。
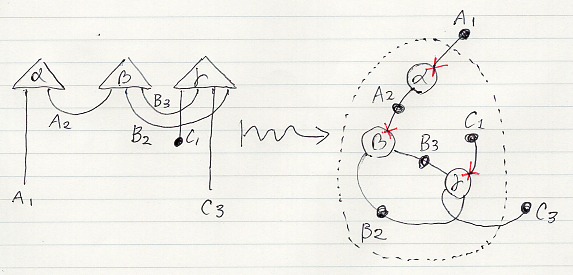
さて、複数のアレンジメントを含むアレンジメント図を作るには、アレンジメントをワイヤーで繋ぐ操作が必要になります。基本になるのは二部アレンジメントをワイヤーで繋ぐ操作で、それを利用して(二部ではない)アレンジメントを繋ぐことになります。というわけで、まずは二部アレンジメントを繋ぐ操作に注目しましょう。
二部アレンジメントの入力部と出力部
Cは条件化可能マルコフ圏だとして、PはCから標準的に構成したマルコフ多圏だとします。Pの対象は、Cの対象のリストであり、モノイド積に関する総積が P → C のモノイド関手を与えます(「アレンジメント計算 4: アレンジメント // マルコフ多圏の基本構造射」参照)。
ω:() → A in P はPのm脚アレンジメントとします。ωから作られる二部アレンジメントは(m+1)個あり、アンパサンド〈アンド記号〉で区切りを入れると、次のように書けます。
- ω:() → A[& 1, ..., m]
- ω:() → A[1 & 2, ..., m]
- ‥‥
- ω:() → A[1, ..., m - 1, &, m]
- ω:() → A[1, ..., m &]
二部アレンジメントの表示には、アレンジメントと区切り位置を示す番号があれば十分です。二部アレンジメントを α = (ω, i/m) のように書くことにします。ここで:
- α は二部アレンジメント
- ω はアレンジメント ω:() → A in P
- m はリストAの長さ、m = length(A) = length(legs(ω)) = length(cod(ω))
- i は区切り位置の番号 0 ≦ i ≦ m
二部アレンジメント α = (ω, i/m) に対して、in(α) と out(α) を次のように定義します。A = legs(ω) = cod(ω) とします。
- in(α) := A[1, ..., i] = (A1, ..., Ai)
- out(α) := A[i + 1, ..., m] = (Ai+1, ..., Am)
要するに、リストAの区切り位置 i より左の部分を取り出したリストが in(α) 、 i より右の部分を取り出したリストが out(α) です。in(α), out(α) が空リストになることがあります。
今まで、脚をグループ分けした二部を、左側の部と右側の部と言ってましたが、入力部〈input part〉、出力部〈output part〉と呼ぶことにします。因子グラフに翻訳するとき、入力部の脚は因子ノードの入力辺、出力部の脚は因子ノードの入力辺に対応します。
マルコフ多圏Pの二部アレンジメントの全体を BipArrgmnt(P) と書きます。二部アレンジメントから二部構造(区切り位置)を忘れれば単なるアレンジメントになります。これは忘却写像といえます。
- Und:BipArrgmnt(P) → Arrgmnt(P) (Und は underlying arrangement から)
in, out は次の形の写像です。
- in:BipArrgmnt(P) → |P|
- out:BipArrgmnt(P) → |P|
二部アレンジメントのリンク積
二部アレンジメントαとβのリンク積〈linked product〉とは、絵で見れば簡単で、αの出力部の脚とβの入力部の脚を繋ぐことです。実際は、さほど簡単な話ではありませんけどね。
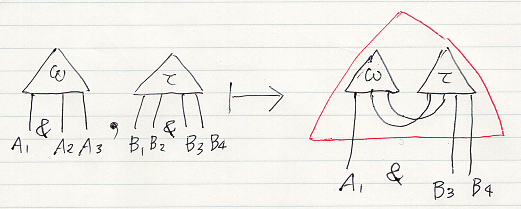
圏の結合〈composition〉は、任意の2つの射に対して定義できるわけではありません。同様に、二部アレンジメントのリンク積も、任意の2つの二部アレンジメントに対して定義できるわけではありません。次の条件が成立するときだけ、αとβのリンク積が定義できます。
- out(α) = in(β)
この条件が成立している前提のもとで、αとβのリンク積を α*β と書きます。中置演算子記号'*'で表現される対応は部分写像です。
- (*):BipArrgmnt(P)×BipArrgmnt(P) ⊃→ BipArrgmnt(P)
記号'⊃→'は部分写像であることを示します。
先ほど「簡単な話ではない」と言いましたが、二部アレンジメントのリンク積の定義には難しいところがあります。リンク積にも結合律や単位律を期待したいのですが、結合律/単位律が成立するようにリンク積を定義することは困難です。結合律/単位律が乱れてしまっていいなら、リンク積は定義できます。
結合律/単位律が成立する積の構成は、BipArrgmnt(P) をそのまま使っていてはウマくいきません。BipArrgmnt(P) 上に“とある同値関係”を入れて、その同値関係による商集合を QBipArrgmnt(P) (Q は quotient から)とします。QBipArrgmnt(P) 上になら望ましリンク積が定義できます。
- (*):QBipArrgmnt(P)×QBipArrgmnt(P) ⊃→ QBipArrgmnt(P)
BipArrgmnt(P) 上のリンク積は、QBipArrgmnt(P) の代表元を選んで計算しているので、等式の意味では結合律や単位律が成立しないのです。(up-to-equivalenceな法則は成立します。)
さらに背後のメカニズムを言えば、マルコフ多圏Pから構成される圏 QRelev(P) があり、QBipArrgmnt(P) Mor(QRelev(P)) (1:1対応がある)になっています。QBipArrgmnt(P) のリンク積は、圏 QRelev(P) の結合に対応します。
ほんとに調べるべき構造は、BipArrgmnt(P) や QBipArrgmnt(P) ではなくて、背後にある圏 QRelev(P) です。そもそも、Arrgmnt(P), BipArrgmnt(P) は確率グラフィカルモデルとのインターフェイスとして準備したものなので、圏論的に自然な構造物とは言えないのです。確率グラフィカルモデルと圏論的確率論とのあいだを Arrgmnt(P), BipArrgmnt(P) を介して多少無理矢理に架橋しようとしているので、Arrgmnt(P), BipArrgmnt(P) の構造に多少の歪みが出るのは致し方ないでしょう。
そういう事情で、リンク積のちゃんとした定義は圏 QRelev(P) を導入してからにします。が、BipArrgmnt(P) 上に(結合律/単位律が乱れる)リンク積が定義できたとして、それから Arrgmnt(P) 上のリンク積をどう作るかは次節で説明します。
アレンジメントのリンク積
アレンジメントのリンク積は、アレンジメントを一旦二部化して、二部アレンジメントのリンク積を取ります。しかし、二部化は一意に決まるわけではなくて、m脚のアレンジメントには(m + 1)個の二部化が可能です。そこで、リンク積の側に二部化の指示を込めてしまい、複数のリンク積を考えます。
アレンジメントのリンク積は、自然数で番号付けられた無限個の演算だとします。それらの演算の中置演算子記号を次のようにします。
- *0, *1, *2, *3, ...
- (*k):Arrgmnt(P)×Arrgmnt(P) ⊃→ Arrgmnt(P) for k = 0, 1, 2, 3, ...
リンク積 (*k) は部分写像なので、リンク積が定義可能である条件を述べる必要があります。ω, τ を、次のような2つのアレンジメントだとします。
- ω:() → A in P, nlegs(ω) = length(A) = m
- τ:() → B in P, nlegs(τ) = length(B) = n
k-リンク積 ω *k τ が定義可能である条件は次のようになります。
1. k ≦ m かつ k ≦ n
2. A[m - k + 1, ..., m] = B[1, ..., k]
つまり、次のように言えます。
- ωの“右のk本の脚”のリストと、τの“左のk本の脚”のリストが等しい。
「k ≦ m かつ k ≦ n」は“k本の脚”のリストを取り出せる条件です。
二部アレンジメント α = (ω, (m - k)/m), β = (τ, k/n) を作ると、それらは二部アレンジメントとして結合可能なのでリンク積 α * β が定義できます。二部アレンジメントの二部構造(区切り位置)を忘れて、アレンジメントを得ます。
- ω *k τ := Und( (ω, (m - k)/m) * (τ, k/n) )
k = 0 のときは無条件に0-リンク積 ω *0 τ が作れて、図で言えば、ωとτを単に並べただけのアレンジメントになります。
おわりに
今回はリンク積が主題だったにも関わらず、リンク積の正体は不明なまま先送りになってしまいました。絵図の操作としてのリンク積は、繋げられるワイヤーを繋ぐだけのことです。しかし、繋ぐ操作の解釈はけっこう難しいってことです。
難しさの要因は、マルコフ圏の条件化可能性公理にあります。条件化可能性公理を仮定すれば、任意の二部アレンジメントにその条件化(の結果)である射を対応付けることができます。が、この対応は一意に決まらないのです。この「条件化の不定性」がいたる所で顔を出します。
「条件化の不定性」をうまく扱える枠組みを作らないと、リンク積もうまく扱えないのです。引き続く話題は、「条件化の不定性」に関わるものになるでしょう(たぶん)。