前回の「アレンジメント計算 7: AlmostSurelyEqual」において、二段ASE〈two-step ASE〉という概念を導入したのですが、この後あれは使わないかもなー(使う可能性も多少はあるけど)。まるっきり無駄だったというのもナンダカラ、計算練習の題材に使おう、っと。
シリーズ第1回 兼 リンクハブ:
マルコフテンソルの圏MarkovTensは、「アレンジメント計算 7: AlmostSurelyEqual // 事例に関して」で述べた圏です。この具体的な圏MarkovTensにおいて、二段ASE がどう書けるかを見ていきましょう。これを例として、ストリング図からテンソルの計算式に翻訳するやり方を説明します。
まず、一時的にですが、実数([0, 1]区間内の実数)の掛け算の記号として '' と '
' の2つの演算子記号を使うことにします。それは、実数の掛け算が何の意味だったかを表すためです。モノイド積〈テンソル積〉由来の掛け算なら '
'、結合由来の掛け算なら '
' を使うことにします。
例えば、idAh の成分表示なら、
のように '' で掛け算を書きます。一方、p;w = w
p の成分表示なら、
とします。さらに、結合が束縛変数〈ダミー変数〉tによって計算されることを明示するために、
のようにしましょう。これで、ストリング図とテンソル計算の対応がだいぶ分かりやすくなります。
さて、 の記述には、次の図をテンソル計算式に翻訳する必要があります。この図には、翻訳のための細工が施されています。
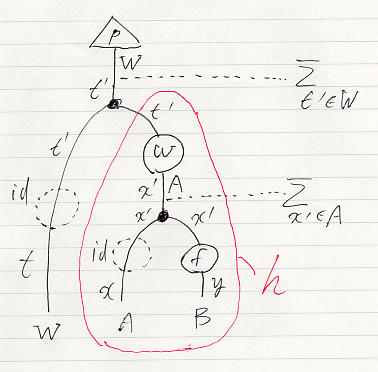
- ワイヤーの脇に使用する変数名をラベルしています。「アレンジメント計算 2: 簡単な実例と注意事項 // 因子グラフ、ストリング図へのラベリング」の約束(変数名をクォートする)は守ってません(苦笑)。
- ワイヤー上の点線の丸は恒等射を表します。恒等射の入力と出力で変数名を変えます。
- 対角〈余乗法 | コピー〉射の三叉には、同じ変数名が3つラベルされています。テンソル計算式では、同じ変数が3回出現することにより対角を表します。
- 右側に注釈されている
は、結合を表現する変数と総和をメモしています。
先に赤い境界で囲まれたクラスター(「アレンジメント計算 3: 絵算の基本技法 // クラスター、ブラックボックス化、反ブラックボックス化」参照)hを考えます*1。h:W → AB in C の成分表示は次のようになります。図の上から下をテキストの左から右へと翻訳します。
- 対角射ΔAが省略さてます。その代わりに対角射を表す変数3回出現に下線を引いています。
- '
'はテンソル積由来の掛け算記号です。
- '
'は結合由来の掛け算記号です。変数名は、総和記号の変数と呼応します。
は、クロネッカーのデルタと同じで、x = x' のところだけが残り他はゼロなので、次のように簡略化できます。
同じ要領で、図の全体は次のように書き下せます。
も同様なので
と簡略化できます。代入すると、
となります。これが絵全体の成分表示です。
今計算した表式を使うと、次の図の二段ASEの関係 は、その下の論理式で書けます。
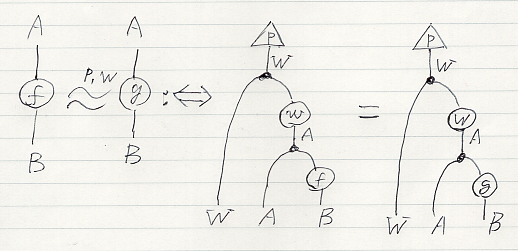
これは次のように書き換えられます。
あるいは:
冒頭で言ったように、この条件は今後使わないかも知れませんが、例題に使ったのでヨシとします。