アレンジメント計算 1：確率グラフィカルモデル - 檜山正幸のキマイラ飼育記 (はてなBlog)

マルコフ圏を気に入ってしまい（「マルコフ圏って、いいんじゃないのコレ」参照）、マルコフ圏の観点からフォング〈Brendan Fong〉の論文 "Causal Theories: A Categorical Perspective on Bayesian Networks" を読み直したりしました（「フォングの“因果セオリー”の理論」参照）。その時期（2020年6月）から、確率グラフィカルモデルが気になるようになりました。例えば、先月（2020年10月）の記事なら：

確率グラフィカルモデルは「グラフィカル」と銘打っているので、なんらかの絵図〈graphics | diagram | picture〉を描きます。しかし、既存の図法は、現象・概念の表現手法としても計算デバイスとしてもイマイチな感じがします。圏論で常用されるストリング図のほうが使い勝手がいいですね（もちろん、僕の圏論バイアスが含まれる意見ですが）。既存の図法はストリング図で置き換えてしまっていいと思います（同じくバイアス付き意見）。

とはいえ、既存の図法とストリング図の相互翻訳は必要でしょう。既存の図法が何種類もあるので、翻訳の構成は大変です*1。

色々な既存の図法 ←(めんどう)→ ストリング図

色々な図法からひつとだけ選んでみます。ストリング図との相性から言うと、因子グラフ（「ストリング図と因子グラフ」参照）が一番良さそうです。

因子グラフ ←(比較的楽)→ ストリング図

それでも、因子グラフとストリング図のあいだのギャップはけっこうあるので、中間にアレンジメント図という図法をはさみます。すると：

因子グラフ ←(楽)→ アレンジメント図 ←(楽)→ ストリング図

アレンジメント図は僕の命名です*2が、特に呼び名がなかっただけで、ジェイコブス〈Bart Jacobs〉やフリッツ〈Tobias Fritz〉もさかんに使っている図法です。アレンジメント図は、形状を制限したストリング図です。任意のアレンジメント図はストリング図なので、次の包含関係があります。

アレンジメント図 ⊂ ストリング図

アレンジメント計算は、アレンジメント図に対する絵算〈{graphical | diagrammatic | pictorial} {calculus | computation}〉です。実際に絵図を描くのはコストがかかるので、テキスト表現／テキスト計算も出来るように工夫します。アレンジメント計算は、絵図から得られる視覚的直観を、マルコフ圏へと正確にマップするメカニズムを提供します。

解説を一度に書く気力は湧かないので、何回かの記事に分けてアレンジメント計算をぼちぼち説明します。今回は、アレンジメント計算で使う特徴的な概念・道具を幾つかピックアップして概説します。

内容：

因子グラフ
アレンジメントとアレンジメント図
マルコフ圏とマルコフ多圏
確率的関連
おわりに

シリーズ：

因子グラフ

最初に因子グラフの話をします。ただし、因子グラフを本気で使う気はなくて、アレンジメント図を説明する補助的素材という位置付けです。なので、説明はラフです。

因子グラフは、ノード〈頂点〉の種類が変数ノード〈変数頂点 | variable {node | vertex}〉と因子ノード〈因子頂点 | factor {node | vertex}〉の二種類ある無向グラフまたは有向グラフです。ここでは、変数ノードを黒丸、因子ノードを白丸で表すことにします（何でもいいですが）。すべてのノードにラベルが付きますが、辺にはラベルが付きません。因子グラフには次の制約があります。

ノード〈頂点〉は有限個である。
2つのノードを結ぶ辺（無向辺または有向辺）は高々1本である。（この性質を持つグラフは単純グラフといいます。）
因子ノードと因子ノードを結ぶ辺は許さない。
辺で結ばれた2つの変数ノードには必ず同じラベルを付ける。（辺で結ばれていない変数ノードに同じラベルを付けても問題ありません。）
ひとつのノード（因子ノードでも変数ノードでも）が持つ辺のあいだにノードごとの全順序（または順序番号）が付いている。（この全順序（番号付け）は明示されずに、暗黙に仮定されることがほとんどです。）

辺が無向辺なら無向因子グラフ〈undirected factor graph〉、辺が有向辺なら有向因子グラフ〈directed factor graph〉です。

次は無向因子グラフの例です。ノードごとの“辺への全順序割り当て”の記述は省略しています。

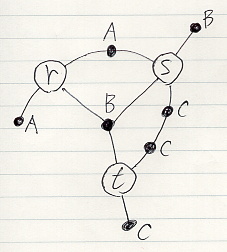
有向因子グラフがサイクルを持たないとき、それは無サイクル有向因子グラフ〈acyclic directed factor graph〉です。無サイクル〈{非 | 無} {輪状 | 循環}〉有向グラフをDAGと略称するので、無サイクル有向因子グラフをDA因子グラフ〈DA factor graph〉または因子DAG〈factor DAG〉とも呼びます。

因子グラフが何を意味するかはケースバイケースですが、簡単な使用例を挙げます。

無向因子グラフ：変数ノードのラベルは集合を表し、因子ノードのラベルは関係（直積集合の部分集合）を表すとする。k本の辺を持つ因子ノードはk項関係を表す。
DA因子グラフ：変数ノードのラベルは集合を表し、因子ノードのラベルは関数を表すとする。「ストリング図と因子グラフ」の例はこのタイプです。

後述のアレンジメント図との相互翻訳をスムーズにするために、因子グラフに境界という概念を付け加えます。視覚的に図示するときは境界を線として描きますが、以下の定義の「境界」は直感的な境界とはズレているかも知れません。

因子グラフ（無向でも有向でもよい）において、ただ1本の辺を持つ〈辺と接続する〉変数ノードを端点〈endpoint〉と呼びます。因子グラフGの端点の集合を Endpoint(G) とします。Endpoint(G) から二元集合 {in, ex} への写像 b:EndPoint(G) → {in, ex} を境界〈boundary〉と呼びます。

b(e) = in である端点を内端点〈internal endpoint〉、b(e) = ex である端点を外端点〈external endpoint〉と呼びます。境界bを添えた因子グラフ (G, b) が境界付き因子グラフ〈factor graph with boundary〉です。

視覚的な図示では、外端点が境界の外部に、内端点が境界の内部になるように境界線を描きます。次は境界付きDA因子グラフの例で、境界線は点線で描いています。ノードごとの“辺への全順序割り当て”の記述は省略しています。

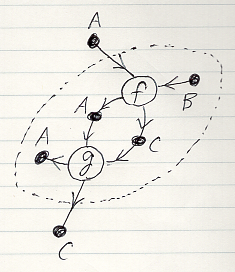
以上で、無向／有向、境界なし／境界付きの因子グラフの説明はオシマイです。この節の冒頭で言ったように、因子グラフを主題的に扱うことはしません。主題はアレンジメント図ですから。説明のために、アレンジメント図を因子グラフに翻訳することはあります。が、実用の目的で、因子グラフを（その他の既存の描画法も）使うのはお薦めしません。細かい不具合があるからです。ストリング図を使いましょう（バイアス付きアドバイス）。

アレンジメントとアレンジメント図

アレンジメント図は、アレンジメントと呼ばれる基本図形（それ自体ストリング図）をワイヤーで繋いで作った図です。アレンジメント〈arrangement〉の形状だけ先に紹介すると、次のような形です（ラベルは省略してます）。

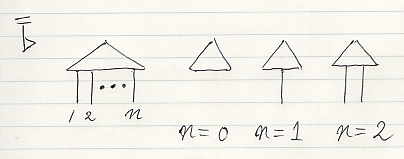
三角形のノードからn本のワイヤーが出た形ですね。上の絵は、描画方向を上から下として描いたものです。左上の“旗”は描画方向を示すものです。他の描画方向で、n = 3 のアレンジメントを描いてみます。

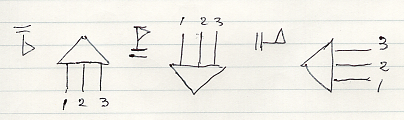
次の図は、長／ジェイコブスの論文 https://arxiv.org/abs/1709.00322 の絵です。描画方向は下から上で、破棄ノード（後述）にはアース記号を使っています。

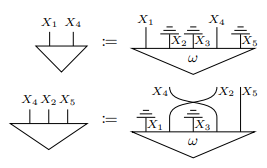
下から上に向かって描くのが多数派ですが、僕は上から下にします（「ボブ・クック教授による、対称とは限らないモノイド閉圏における絵の描き方」に上から下の例があります）。

アレンジメントから出ているワイヤーを脚〈leg〉と呼びます。n本の脚を持つアレンジメントをn脚アレンジメント〈n-leg arrangement〉といいます。

アレンジメントの脚〈ワイヤー〉の交差、分岐（二又）、破棄が許されます*3。ワイヤー内をデータ・情報が流れると想定すると、分岐はデータ・情報をコピーすることに対応し、破棄はデータ・情報を捨てて利用できなくすることに対応します。（[追記 date="翌日"]目的によっては分岐は禁止される可能性があります。[/追記]）

また、2つのアレンジメントを横に併置すること、ワイヤーを繋ぐ〈リンクする〉こともできます。複数のアレンジメントの位置関係〈レイアウト〉はある程度は変更できます。見やすいレイアウトを選べます。

幾つかのアレンジメントを適当に配置して、ワイヤーの交差・分岐・破棄・接続により組み合わせた図がアレンジメント図〈arrangement diagram〉です。ただ1つのアレンジメントだけの図も、何もない“空な図”もアレンジメント図です。

任意のアレンジメント図を、単一のアレンジメントだとみなすことができます。アレンジメント図の構成・構造を隠蔽して単一のアレンジメントだとみなすことを、アレンジメント図のブラックボックス化〈blackboxing〉といいます。

与えられたアレンジメント図に対して、「アレンジメント $\mapsto$ 因子ノード、ワイヤー／分岐／破棄 $\mapsto$ 変数ノード」と対応付けることにより、境界付き無向因子グラフに翻訳〈変換〉できます。今、翻訳の規則を述べることはしまんせが、例をひとつ挙げます。因子ノードにおける“辺への全順序割り当て”だけ番号で記述しています。

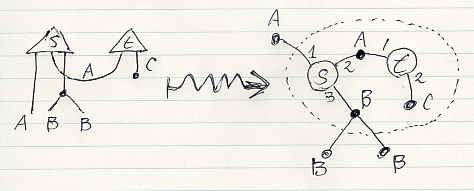
マルコフ圏とマルコフ多圏

アレンジメント図は、ストリング図の一種です（形状の自由度が制限されている）。ストリング図に対して、その解釈（意味論）の場が必要です。今後描かれるストリング図（アレンジメント図含む）は、とあるマルコフ圏Cにおいて解釈されます（後でより便利な圏に変更しますが）。マルコフ圏については、次の記事とそこから参照されている記事達を参照してください。

マルコフ圏 A First Look -- 圏論的確率論の最良の定式化

ストリング図／アレンジメント図が解釈される場であるマルコフ圏Cは、単なるプレーンなマルコフ圏ではなくて、条件化可能性を持つ（条件化可能マルコフ圏だ）と仮定します。したがって、反転可能性も持ちます*4。条件化可能性〈条件化可能公理 | conditionalizable axiom〉、反転可能性〈convertible axiom | 反転可能公理〉については次の記事に書いてあります。

ストリング図／アレンジメント図を、条件化可能マルコフ圏Cにおいて直接解釈〈意味付け〉すると微妙に不便なところがあります*5。Cと密接に関係する簡約多圏〈reduced polycategory〉（「対称モノイド多圏（簡約版）」参照）Pにおいて解釈すると幸せになれます。

「Cにおいて解釈」している状況でも、実際のところは（潜在的に）「Pにおいて解釈」を使っています。であるならば、最初から明示的に「Pにおいて解釈」したほうがいいでしょう。モノイド圏（または対称モノイド圏）から簡約多圏を構成する方法と関連する話題は次の記事にあります。

もとになるモノイド圏Cと対応する簡約多圏Pとの関係は、直感的には理解出来ると思います。が、その背後にはモノイド圏の一貫性理論／一貫性定理〈coherence theory / coherence theorem〉があるので、正確な主張や証明はなかなか難しいです。いつか正確な話もしたいですが、とりあえず難しいことは気にせずに、簡約多圏Pを道具として使えればよいという態度もアリだと思います。

簡約多圏Pは、モノイド圏Cの厳密化〈strictification〉モノイド圏になっているので、その観点からCとPの関係を述べておくのは参考になるかも知れません。CとPのめぼしい特徴は：

|P| = |C|^* = List(|C|) である。
Pは厳密モノイド圏で、Pのモノイド積の対象部分は、List(|C|) の連接演算に一致する。
タイト・モノイド関手 S = (S, μ^S, ε^S) :C → P と、タイト・モノイド関手 Π = (Π, μ^Π, ε^Π) :P → C があり、S, Π により、CとPはモノイド圏として圏同値〈モノイド圏同値〉である。タイト・モノイド関手については「モナド論をヒントに圏論をする（弱2-圏の割と詳しい説明付き）」参照。
S＊Π = Id_C が成立する。ここで、'＊'は関手の図式順結合記号、Id_C は恒等関手。
モノイド圏同値を与える自然同型〈可逆自然変換〉ι::Id_P ⇒ Π＊S: P → P の成分 ι_A∈P(A, (Π(A))) = C(Π(A), Π(A)) は恒等射で与えられる。（AはPの対象、つまりCの対象のリストです。）

マルコフ圏Cから構成された厳密モノイド圏である簡約多圏Pを、マルコフ多圏〈Markov polycategory〉と呼ぶことにします。本物の多圏ではなくて簡約多圏ですが、リストを対象〈多対象〉とする意味では“多圏”と呼んでもいいでしょう。マルコフ圏Cをそのまま扱う代わりにマルコフ多圏Pを使うことにします。タイト・モノイド関手 Π:P → C があるので、必要なら（必要でなくても）P上の概念をC上に移して考えることができます。この意味では、おおむねC上で解釈していると言えます。

確率的関連

アレンジメントはストリング図ですが、そのストリング図をマルコフ多圏Pで解釈したものもまた（Pの）アレンジメントと呼びます。Pのアレンジメントは、ω:() → A in P （A ∈|P|）という形の射です。() は、Pの単位対象である空リストです。Pのアレンジメントの全体を Arrgmnt(P) とします。定義から Arrgmnt(P) ⊆ Mor(P) です。

集合（大きい集合かも知れない）Arrgmnt(P) は圏ではありません。が、集合 Arrgmnt(P) に幾つかの演算を導入できて、ある種の代数系として扱えます。代数系としての Arrgmnt(P) は、機能的には圏と似ています。その理由は、Arrgmnt(P) の背後に圏があって、Arrgmnt(P) がその圏の対象類になっているからです。

問題の圏を Relev(P) と書きます。"Relev" は relevance〈関連〉からです（定義はすぐ後で）。Relev(P) は、マルコフ多圏Pから構成される圏です。Relev(P) はPの部分圏ではありませんが、Pへの忘却関手を持ちます。そして、|Relev(P)| = Arrgmnt(P) が成立します。

話を具体的にするために、Cが具体的に構成された確率的マルコフ圏（ジリィモナドのクライスリ圏の部分マルコフ圏）だとします。このとき、Cの対象は可測空間で、Cの射はマルコフ核（「マルコフ核：確率計算のモダンな体系」参照）です。PはCを厳密化・多圏化したマルコフ多圏です。この状況で、Relev(P) がどんな圏であるかを説明します。

圏論の標準的語彙を使うなら、Relev(P) の定義は非常に簡単で：

Relev(P) := ^()/P

右辺は、Pの単位対象 ()（空リスト）に対するアンダー圏〈余スライス圏〉（「オーバー圏、アンダー圏」参照）です。PはCと圏同値なので、^()/P は ^1/C と事実上同じです。

Pのアレンジメントの定義とアンダー圏の定義を照合すれば、Arrgmnt(P) = |Relev(P)| は明らかです。“Relev(P) の対象＝Pのアレンジメント” ω:() → (A₁, ..., A_n) は、Pが確率的マルコフ多圏の場合、次のように言えます。

ωは、可測空間 A₁ $\otimes$ ... $\otimes$ A_n 上の確率測度。
ωは、可測空間達 A₁, ..., A_n に値を取る同時確率分布。
(A₁ $\otimes$ ... $\otimes$ A_n, ω) は確率空間。

どれも同じことですが、「Relev(P) の対象は確率空間」と言うことにします。この言い方を使うなら、アレンジメント（の意味）も確率空間です。もちろん、他の言葉を使っても事実は変わりません。

Relev(P) := ^()/P という定義から、Relev(P) の射 F:(ω:() → (A₁, ...,A_n)) → (τ:() → (B₁, ..., B_m)) in Relev(P) は次の図式を可換にするPの射です。

$\require{AMScd} \begin{CD} () @= () \\ @V{\omega}VV @VV{\tau}V \\ (A_1, \cdots, A_n) @>{F}>> (B_1, \cdots, B_m) \end{CD}$

Cで考えれば、Fは次の図式を可換にするCの射です。

$\require{AMScd} \begin{CD} {\bf 1} @= {\bf 1} \\ @V{\omega}VV @VV{\tau}V \\ A_1\otimes \cdots \otimes A_n @>{F}>> B_1\otimes \cdots \otimes B_m \end{CD}$

Relev(P) := ^()/P の射を関連〈relevance〉と呼ぶことにします*6。Pが確率的マルコフ多圏の場合は確率的関連〈probabilistic relevance〉と言えます*7。確率的関連は、Relev(P) の対象である確率空間のあいだのマルコフ核で、確率測度を保存するものです。つまり、Relev(P) は、確率空間と確率測度保存マルコフ核の圏です。

アレンジメントの集合 Arrgmnt(P) は、圏 Relev(P) の対象の集合ですが、単なる集合ではなくて、Relev(P) の圏構造を反映した代数構造を持ちます。Relev(P) に関する情報は、すべて Arrgment(P) の代数構造としてエンコードされていると言えます。したがって、Arrgmnt(P) の代数構造を調べれば、Relev(P) のことも完全に分かります。

[追記 date="翌日"]代数構造を備えた Arrgmnt(P) と圏 Relev(P) は同一の概念的実体の異なる現れ方なのでしょう。圏 Relev(P) は、条件化可能マルコフ多圏Pへの忘却関手を持つので、P上の具象圏〈concrete category〉です。Relev(P) は対称モノイド構造を持ち、忘却関手は対称モノイド構造を移すタイト・モノイド関手になります。しかし、Relev(P) はマルコフ圏（あるいはマルコフ多圏）にはなりません。その代わりダガー構造を持ちます。Relev(P) とP、そして Arrgmnt(P) の相互関係は意外と込み入っているようです。[/追記]

おわりに

確率グラフィカルモデルの絵図としてアレンジメント図（ストリング図の一種）を使う際に、絵図の意味は Arrgmnt(P) で解釈します。Arrgmnt(P) は圏ではありませんが、圏 Relev(P) の対象類になっています。Relev(P) はマルコフ多圏Pから作られます。そしてPは条件化可能マルコフ圏Cから作られます。ひとつの圏ではなくて、C, P, Relev(P) と複数の圏が出現します。

今回は触れませんでしたが、圏 Relev(P) と圏同型になる圏 Couple(P)（カップルの圏、「ベイズ確率論とデータベース理論の統合：カップル化可能圏 // カップルの圏」参照）、Relev(P) を同値関係「ほとんど等しい〈almost surely equal〉」で割ったダガー圏（「確率グラフィカルモデルの背後にある圏は何か？」に少し書いています）なども絡んできます。

確率グラフィカルモデルの意味論は、幾つかの圏達が互いに絡みあった意味的構造物を使って行う必要があるようです。次回は、Arrgmnt(P) の代数構造について述べる予定です。

*1:「確率グラフィカルモデルの背後にある圏は何か？」で、図の翻訳に触れています。

*2:当初はカップリング図と呼んでいました。が、カップルを別な意味で使うことにしたので、アレンジメントに変えました。

*3:交差、分岐、破棄もストリング図のノードです。特殊なノードなので、これらのノードをスパイダー{ノード}?〈spider {node}?〉と呼びます

*4:「反転可能ならば条件化可能」も成立するようです。 https://arxiv.org/pdf/1709.00322.pdf の p.11 Proposition 3.10 参照

*5:例えば、モノイド圏の結合律子 α 、左右の単位律子 λ, ρ を考慮するのは鬱陶しいですね。

*6:当初は影響〈influence〉と呼んでいました。が、influence〈影響〉とinference〈推論〉が紛らわしいので、関連〈relevance〉に変えました。

*7:ベイズネットワーク界隈では因果関係と呼ばれるものです。「因果関係」はあまりにミスリーディングなので使いたくないです。