$`\newcommand{\cat}[1]{\mathcal{#1} }
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\lexp}{\triangleright }
\newcommand{\rexp}{\triangleleft }
\newcommand{\In}{\text{ in } }
%`$圏論に現れるモノやコトを視覚的に表す描画法として、ストリング図とペースティング図があります。もうひとつの描画法としてハイパーグラフ図を紹介します。
内容:
圏論の描画法
ストリング図とペースティング図は一長一短があり、ストリング図を完全にペースティング図で置き換えるわけにはいかないし、ペースティング図を完全にストリング図で置き換えることも出来ません。
ハイパーグラフ図は、ストリング図とかなり似ているので、僕は積極的にハイパーグラフ図を使うことはなかったのですが、次の二点はハイパーグラフ図を使うべき理由になります。
- 分野によっては、ハイパーグラフ図に類似の描画法が標準になっている。
- モノイド閉圏のカリー化/反カリー化の描画がわかりやすい。
最近、上記の二点が共に当てはまる状況に遭遇しました。これはハイパーグラフ図を使うべきだな、と思いました。
以下に、ハイパーグラフ図の説明をします。しかし、圏論的背景をいちいち説明はしません。ここでまとめて手短に言っておきます。
- モノイド圏 $`\cat{C} = (\cat{C}, \otimes, I)`$ を考える。
- モノイド積に対して左右の指数〈内部ホム〉演算 $`\lexp`$ と $`\rexp`$ があり、この指数演算により $`\cat{C}`$ はモノイド閉圏になっている。つまり次が成立する。
$`\quad \cat{C}(A\otimes B, C) \cong \cat{C}(A, C\rexp B) \cong \cat{C}(B, A\lexp C)`$ - 左右の指数演算を準備したので、モノイド積が非対称でも対応できるが、実際には対称モノイド圏を扱う。
- $`\cat{C}`$ の対象のリストを改めて対象とすることにより、モノイド圏の厳密化〈strictification〉ができる。この方法で厳密化したモノイド圏を $`\mrm{Seq}(\cat{C})`$ とする。
- ストリング図やハイパーグラフ図は、厳密モノイド閉圏 $`\mrm{Seq}(\cat{C})`$ の射を表す目的で使う。
ハイパーグラフ
まず、有向グラフの復習をしておきましょう。$`G = (E, V, \mrm{src}, \mrm{targ})`$ が有向グラフ〈directed graph〉だとは:
- $`E, V`$ は集合。
- $`\mrm{src}:E \to V`$ は写像。
- $`\mrm{trg}:E \to V`$ は写像。
構成素の呼び名は:
- $`E`$ は{有向}?辺〈{directed}? edge〉の集合
- $`V`$ は頂点〈vertex〉の集合
- $`\mrm{src}`$ は始頂点写像〈source map〉
- $`\mrm{trg}`$ は終頂点写像〈target map〉
有向グラフしか扱わない文脈では、単にグラフ〈graph〉と言っても有向グラフのことです。
グラフの始頂点写像、終頂点写像は、辺にそれぞれひとつの頂点を対応させますが、頂点のコレクションを対応させるように変更しましょう。典型的なコレクションには次があります。
- 頂点の集合
- 頂点のバッグ
- 頂点のリスト
ここでは頂点のリストを使います。つまり、{有向}?グラフの定義を次のように変更します。
- $`E, V`$ は集合。
- $`\mrm{src}:E \to \mrm{List}(V)`$ は写像。
- $`\mrm{trg}:E \to \mrm{List}(V)`$ は写像。
変更した後のグラフは順序付き有向ハイパーグラフ〈ordered directed hypergraph〉といいます。集合 $`E`$ の要素はハイパー{有向}?辺〈directed hyperedge〉と呼びます。
リスト以外のコレクションを使ったハイパーグラフは、たぶん次のように呼ぶのでしょう。
- 頂点の集合を使用: 順序無し有向ハイパーグラフ
- 頂点のバッグを使用: {重複度 | 多重度}付き順序なし有向ハイパーグラフ
ここでは、順序付き有向ハイパーグラフしか考えません。よって、単にハイパーグラフ〈graph〉と言えば順序付き有向ハイパーグラフのことです。ハイパー辺はハイパー有向辺です。
多射とハイパー辺
$`\cat{C} = (\cat{C}, \otimes, I)`$ (記号の乱用)はモノイド圏とします。次の書き方を使います。
$`\quad f:(A_1, \cdots, A_n) \to (B_1, \cdots, B_m) \In \mrm{Seq}(\cat{C})`$
これは次の意味です。
- $`A_1, \cdots, A_n \in |\cat{C}|`$
- $`B_1, \cdots, B_m \in |\cat{C}|`$
- $`f \in \cat{C}(A_1\otimes \cdots\otimes A_n, B_1\otimes \cdots\otimes B_m)`$
空リストは単位対象 $`I`$ を意味し、長さ1のリスト $`(A)`$ は対象 $`A`$ と同一視してかまいません。
この形の射を多射と呼びます。英語なら polymorphism が自然ですが、「多相の意味の polymorphism」と被るので polyarrow とか polymap が多いようです。
$`\cat{C}`$ のリストの全体と多射の全体は再びモノイド圏になります。それを $`\mrm {Seq}(\cat{C})`$ と書いています。圏 $`\mrm{Seq}(\cat{C})`$ の $`\mrm{dom}, \mrm{cod}`$ は次のようになります。
- $`\mrm{dom}: \mrm{Mor}(\mrm{Seq}(\cat{C})) \to \mrm{List}(|\cat{C}|)`$
- $`\mrm{cod}: \mrm{Mor}(\mrm{Seq}(\cat{C})) \to \mrm{List}(|\cat{C}|)`$
多射($`\mrm{Mor}(\mrm{Seq}(\cat{C}))`$ の要素)をハイパー辺、$`\cat{C}`$ の対象を頂点と考えると、$`\mrm{dom}, \mrm{cod}`$ によりハイパーグラフが定義できます。
- $`\cat{C}`$ の対象は頂点とみなせる。
- $`\mrm{Seq}(\cat{C})`$ の射〈多射〉はハイパー辺とみなせる。
ハイパー辺の描画法
前節までに説明した状況設定で、多射をハイパー辺として描画しましょう。多射をハイパ辺(正確には順序付き有向ハイパーグラフの有向ハイパー辺)として描く描画法/描かれた図をハイパーグラフ図〈hypergraph diagram〉と呼びます。
まず、$`\cat{C}`$ の対象は白丸(なかを塗らない丸)で描きます。頂点ラベルは白丸のなか、または白丸のそばに書きます。ハイパー辺は小さな黒丸で代表させて、域の対象達、余域の対象達を線で結びます。$`f:(A, B) \to (C, D, E)`$ なら次のようです。下の2つの図はレイアウトが違うだけで同じものです。
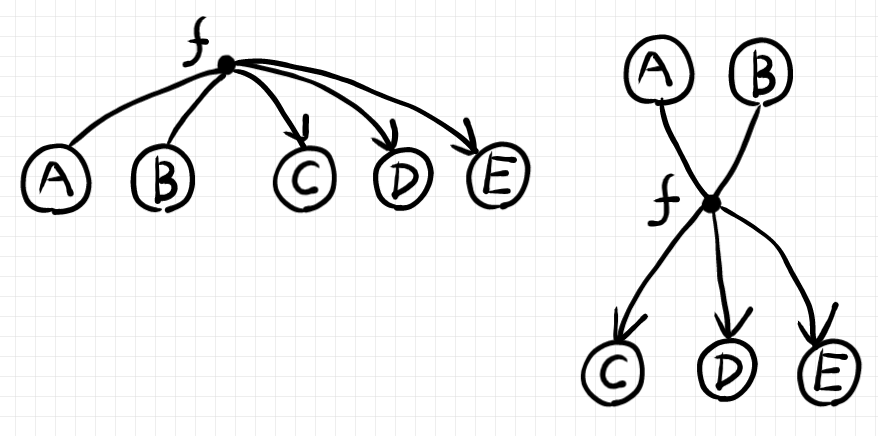
向きが分かるように、矢印の先〈アローヘッド〉('>'の形)は描きます。
ハイパーグラフ図で描いた多射と、ストリング図で描いた多射の関係は明らかでしょう。
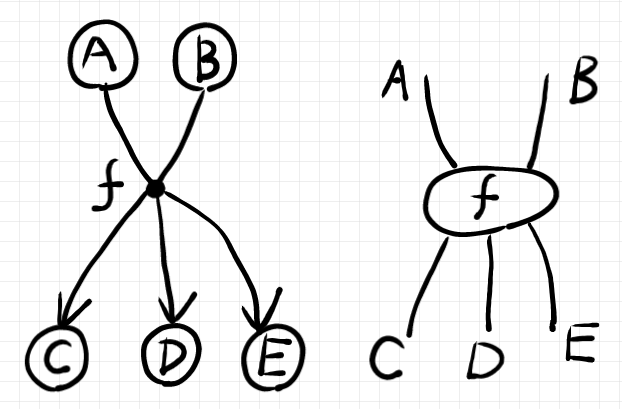
注意事項として、矢印の線やアローヘッドを、白丸のなかに入れないようにしてください。なかに侵入する矢印は後で別な意味で使うつもりなので。
モノイド積と指数
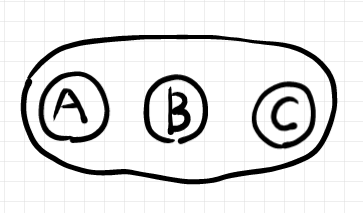
左から右に並べた幾つかの白丸をひとつの白丸で囲むと、それはモノイド積を表します。例えば、左から右に並べた $`A, B, C`$ を囲むと $`A\otimes B\otimes C`$ を意味します。
単位対象 $`I`$ は特に白い星印で表すことにします。$`I \otimes A \cong A`$ を描くと次のようになります。
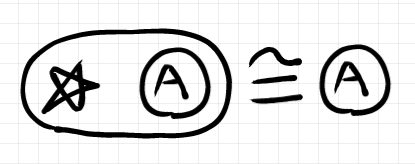
指数対象 $`A \lexp B`$ 、$`A \rexp B`$ は次のように描きます。
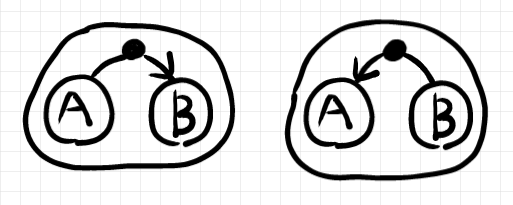
ここで、白丸内のハイパー辺は単一特定の多射を表しているわけではありません。外側の白丸が指数対象であることを示しています。幾つかのプログラミング言語で、アロー関数(ラムダ式による無名関数)と関数型を表すアローに同じアローを使っているのと同様な事情です。
対象 $`(A\otimes B) \lexp C`$ なら次のように描きます。
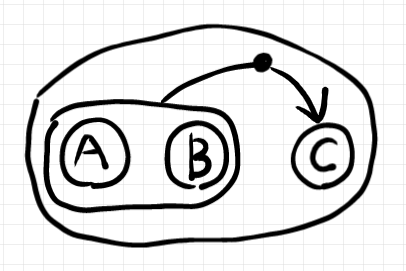
カリー化と反カリー化
モノイド圏 $`\cat{C}`$ がモノイド閉のとき、次のようなホムセット間の同型射があります。
- $`\mrm{Seq}(\cat{C})( (B), (A\lexp C)) \to \cat{C}(B, A\lexp C) \In {\bf Set}`$
- $`\cat{C}(B, A\lexp C) \to \cat{C}(A\otimes B, C) \In {\bf Set}`$
- $`\cat{C}(A\otimes B, C) \to \mrm{Seq}(\cat{C})( (A, B), (C)) \In {\bf Set}`$
これらを繋ぐと、次の同型になります。これは、圏(あるいは多圏) $`\mrm{Seq}(\cat{C})`$ における左反カリー化です。
$`\quad \mrm{Seq}(\cat{C})( (B), (A\lexp C)) \to \mrm{Seq}(\cat{C})( (A, B), (C)) \In {\bf Set}`$
この左反カリー化をハイパーグラフ図の書き換え〈描き換え | 変形〉として描くと次のようになります。グニョグニョした矢印は書き換えを表します。
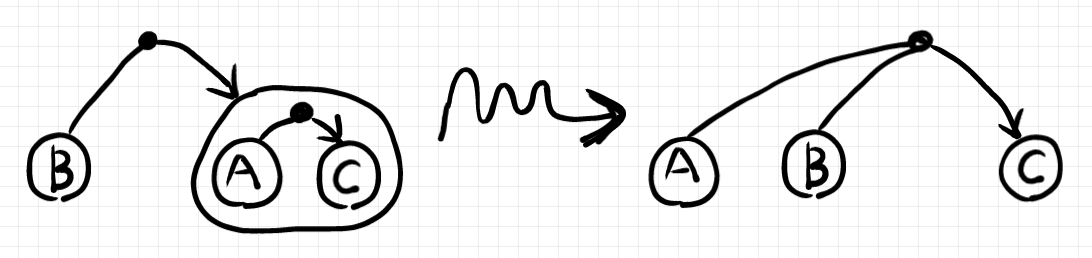
テキストとして写し取れば:
$`\quad (f: (B) \to (A\lexp C)) \leadsto ( {_\cup f} :(A, B) \to C)`$
ここで、$`{_\cup f}`$ は $`f`$ の左反カリー化を表します。ただし、$`{_\cup f}`$ という書き方は、上から下に描くストリング図に基づく“象形文字”なので、ハイパーグラフ図だとピンとこないかも知れません。
右反カリー化、あるいは左右のカリー化も同様です。
ハイパーグラフ図では、入れ子になった白丸の操作でカリー化/反カリー化が比較的容易に描けます。カリー化/反カリー化を多用する場合はハイパーグラフ図が便利でしょう。