「環境付き計算と依存アクテゴリー 2/n」の続きです。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{\text{ in }}
%\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\twoto}{ \Rightarrow }
\newcommand{\id}{ \mathrm{id} }
\newcommand{\hyp}{\text{-} }
\newcommand{\NFProd}[3]{ \mathop{_{#1} \!\underset{#2}{\times}\,\!_{#3} } }
\newcommand{\dcat}[1]{\mathbb{#1}}
\newcommand{\coupl}{ \circledast }
`$
内容:
ハブ記事:
依存アクテゴリー: 復習
依存アクテゴリーとは、いやっ、僕が依存アクテゴリーだろうと想定している構造とは、一言でいえば、
- 左脚がファイブレーションであるスパン上に載った二重圏構造
です。
今までに、次の素材は定義しています。
- デカルト圏 $`\cat{C}`$
- 圏 $`\cat{E}`$ と、ファイブレーション(射影関手) $`\mrm{Proj} : \cat{E} \to \cat{C}`$
- ミックス関手 $`\mrm{Mix} : \cat{E} \to \cat{C}`$
- 自明持ち上げ関手 $`\mrm{TLift} : \cat{C} \to \cat{E}`$
- 写像のペア(まだ関手であることは示してない)
$`\quad \mrm{Coupl} : \mrm{Mor}(\cat{E})\times_{\mrm{Mor}(\cat{C})} \mrm{Mor}(\cat{E}) \to \mrm{Mor}(\cat{E})`$
$`\quad \mrm{Coupl} : |\cat{E}|\times_{|\cat{C}|} |\cat{E}| \to |\cat{E}|`$
残っている作業は次です。
- 写像のペア(2つの写像の名前をオーバーロードしている)$`\mrm{Coupl}`$ が関手であることを示す。
- 関手達 $`\mrm{Proj}, \mrm{Mix}, \mrm{TLift}, \mrm{Coupl}`$ が二重圏を形成することを示す。
$`\mrm{Proj}, \mrm{Mix}`$ が作るスパンの左脚 $`\mrm{Proj}`$ がファイブレーションであることは既に分かっている(「環境付き計算と依存アクテゴリー 1/n」参照)ので、上記の2つの作業が完了すれば、以下の構造が依存アクテゴリーであることが確認できます。
$`\quad (\cat{C}, \cat{E}, \mrm{Proj}, \mrm{Mix}, \mrm{TLift}, \mrm{Coupl})`$
圏のファイバー積とファイバー双関手性
「依存アクテゴリーに向けて // 一貫性地獄」で述べたような事情から、圏達の2-圏 $`{\bf CAT}`$ 内のファイバー積の定義は一意には決まりません(「ファイバー積対象が一意に決まらない」こととは別!)。ここでは、プルバック四角形が厳密可換(等式で表現可能)な厳密プルバックによりファイバー積を定義します。
より具体的に言えば、圏 $`\cat{X}`$ と圏 $`\cat{Y}`$ の(コスパンによる)ファイバー積を、対象集合のファイバー積と射集合のファイバー積から定義します。次の図式を考えましょう。
$`\quad \xymatrix{
{}
& \cat{W} \ar[dl]_{P_1} \ar[dr]^{P_2}
\ar@{}[dd]|{\text{p.b.}}
& {}
\\
\cat{X} \ar[dr]_F
& {}
& \cat{Y} \ar[dl]^G
\\
{}
& \cat{Z}
& {}
}\\
\quad \In {\bf CAT}`$
上記の図式の $`\cat{W}, P_1, P_2`$ を以下の2つのプルバック図式から構成します。
$`\quad \xymatrix{
{}
& |\cat{W}| \ar[dl]_{(P_1)_\mrm{obj} } \ar[dr]^{(P_2)_\mrm{obj} }
\ar@{}[dd]|{\text{p.b.}}
& {}
\\
|\cat{X}| \ar[dr]_{F_\mrm{obj} }
& {}
& |\cat{Y}| \ar[dl]^{G_\mrm{obj} }
\\
{}
& |\cat{Z}|
& {}
}\\
%
\:\\
\quad \xymatrix{
{}
& \mrm{Mor}(\cat{W}) \ar[dl]_{(P_1)_\mrm{mor} } \ar[dr]^{(P_2)_\mrm{mor} }
\ar@{}[dd]|{\text{p.b.}}
& {}
\\
\mrm{Mor}(\cat{X}) \ar[dr]_{F_\mrm{mor} }
& {}
& \mrm{Mor}(\cat{Y}) \ar[dl]^{G_\mrm{mor} }
\\
{}
& \mrm{Mor}(\cat{Z})
& {}
}\\
\quad \In {\bf SET}`$
(大きい集合達の)集合圏のなかのファイバー積は具体的に記述できます。例えば:
$`\quad |\cat{W}| := \{(X, Y) \in |\cat{X}|\times |\cat{Y}| \mid F_\mrm{obj}(X) = G_\mrm{obj}(Y) \}`$
このようにして作った $`(|\cat{X}|\times_{|\cat{Z}|}\cat{Y}, \mrm{Mor}(\cat{X})\times_{\mrm{Mor}(\cat{Z})} \mrm{Mor}(\cat{Y}))`$ 上に圏の構造がちゃんと載ることは確認する必要がありますが、具体的な定義に基づいて示せます。
集合圏の厳密プルバック(集合圏では厳密プルバックしかない)をもとに構成した圏のファイバー積を厳密ファイバー積〈strict {fiber | fibered} product〉と呼びましょう。厳密ファイバー積であっても、一般的には一意性は保証できませんが、具体的な構成法を決めれば一意的に具体的なファイバー積が決まるとしてかまいません。
$`\cat{X}\times_{\cat{Z}}\cat{Y} = \cat{X}\NFProd{F}{\cat{Z}}{G} \cat{Y}`$ は、今説明した厳密ファイバー積のことだとします。$`\cat{X}\times_{\cat{Z}}\cat{Y}`$ の対象と射は次のようなペアとして表現できます。
$`\quad (X, Y)\in |\cat{X}\times_{\cat{Z}}\cat{Y}|
\iff X\in |\cat{X}|, Y\in |\cat{Y}|, F(X) = G(Y)\\
\quad (f, g)\in \mrm{Mor}(\cat{X}\times_{\cat{Z}}\cat{Y})
\iff f \in \mrm{Mor}(X), g \in \mrm{Mor}(Y), F(f) = G(g)
`$
$`H: \cat{X}\times_{\cat{Z}}\cat{Y} \to \cat{V}`$ が、ファイバー積の意味での双関手〈二項関手〉であることは、通常の双関手性と同じように記述できます。
$`\text{For }(f, g) : (X, Y) \to (X', Y') \in \cat{X}\times_{\cat{Z}}\cat{Y}\\
\text{For }(f', g') : (X', Y') \to (X'', Y'') \in \cat{X}\times_{\cat{Z}}\cat{Y}\\
\quad H( (f, g) ; (f', g')) = H( (f; f', g; g')) = H(f, g); H(f', g') \\
\text{For } (X, Y) \in |\cat{X}\times_{\cat{Z}}\cat{Y}|\\
\quad H( \id_{(X, Y)}) = H( (\id_X, \id_Y) ) = \id_{H(X, Y)}
`$
$`H`$ を中置演算子記号 $`\odot`$ で書いた場合は、ファイバー積の意味での双関手性の等式は次のようになります。
$`\quad (f; f')\odot (g; g') = (f \odot g); (f'\odot g') \\
\quad \id_X \odot \id_Y = \id_{X \odot Y}
`$
上記の形で定義される「ファイバー積の意味での双関手〈二項関手〉である」という性質をファイバー双関手性〈{fiber | fibered} bifunctoriality〉と呼びましょう。ファイバー双関手性を満たす関手はファイバー双関手〈{fiber | fibered} bifunctor〉です。
ファイバー双関手性/ファイバー双関手は、実際は単なる関手性/関手なのですが、関手の域〈ソース〉がファイバー積であることを強調・意識した呼び名です。
モノイド圏の場合
前節で述べたように、2つの圏 $`\cat{X}, \cat{Y}`$ の具体的な厳密ファイバー積 $`\cat{X}\times_{\cat{Z}}\cat{Y} = \cat{X}\NFProd{F}{\cat{Z}}{G} \cat{Y}`$ の上で定義された写像がファイバー双関手〈ファイバー二項関手〉であることは、対象・射をペアで書いて、写像を二項中置演算子記号 '$`\odot`$' を使って書けば、交替法則〈interchange law〉の形に書けます。
モノイド圏のモノイド積の交替法則〈交替律〉も、ファイバー双関手性の特別なケースです。それを確認しましょう。
特定された単元集合〈distinguished singleton set〉を $`{\bf 1}`$ とします。単一対象・単一射の自明圏〈trivial category〉も同じ記号をオーバーロードして $`{\bf 1}`$ と書きます。任意の圏 $`\cat{X}`$ から自明圏 $`{\bf 1}`$ への唯一の関手も、集合の場合の記号をオーバーロードして $`!_\cat{X}`$ とします。
$`\cat{X} = (\cat{X}, \otimes, \mrm{I})`$ (記号の乱用)がモノイド圏のとき、モノイド積双関手 $`(\otimes)`$ は、次の形にも書けます。
$`\quad (\otimes) : \cat{X}\times_{{\bf 1}}\cat{X} \to \cat{X} \In {\bf CAT}`$
もちろんこれは、次の一般的同型があるからです*1。
$`\quad \cat{X}\times_{ {\bf 1}}\cat{Y} = \cat{X}\NFProd{!_{\cat{X}}}{ {\bf 1} }{!_{\cat{Y}} } \cat{Y} \cong \cat{X}\times \cat{Y} \In {\bf CAT}`$
この状況でのファイバー双関手性は次の等式達です。
$`\quad (f; f')\otimes (g; g') = (f \otimes g); (f'\otimes g') \\
\quad \id_X \otimes \id_Y = \id_{X \otimes Y}
`$
これは、モノイド圏のモノイド積の交替法則に他なりません。
二重圏は、圏のファイバー積により定義されます。自明圏の上のファイバー積により構成された二重圏はモノイド圏です。言い方を変えれば、タイト射の圏が自明圏である二重圏はモノイド圏です。
自明圏の上のファイバー積=直積の第一射影(下)はファイブレーションとなります。
$`\quad P_1 : \cat{X}\times_{ {\bf 1}}\cat{X} \to \cat{X} \In {\bf CAT}`$
このことから、通常のモノイド圏は、依存アクテゴリー(ファイブレーションを備えた二重圏)の事例となることが分かります。
環境付き計算ペアのカップリングのファイバー双関手性
今のところ、環境付き計算ペアのカップリングは、次のような“写像”です。
$`\quad (\coupl) = \mrm{Coupl} \; : \cat{E}\times_{\cat{C}}\cat{E} \to \cat{E}`$
これは、2つの写像を横着してまとめて書いているので、ちゃんと分けて書けば:
$`\quad \mrm{Coupl}_\mrm{obj} : |\cat{E}|\times_{|\cat{C}|}|\cat{E}| \to |\cat{E}| \In {\bf SET}\\
\quad \mrm{Coupl}_\mrm{mor} : \mrm{Mor}(\cat{E})\times_{\mrm{Mor}(\cat{C}) } \mrm{Mor}(\cat{E}) \to \mrm{Mor}(\cat{E}) \In {\bf SET}\
`$
この“写像”が関手であることを確認するには、前々節で述べたファイバー双関手性を示す必要があります。ファイバー双関手性は交替法則の形で書けるので、交替法則を示すと言っても同じです。
4つの環境付き計算ペア($`\cat{E}`$ の射)$`f, g, f', g'`$ と2つの対象ペア($`\cat{E}`$ の対象) $`(S, A), (T, B)`$に対して、次の等式が交替法則です。
$`\quad (f; f')\coupl (g; g') = (f \coupl g); (f'\coupl g') \\
\quad \id_{(S, A)} \coupl \id_{(T, B)} = \id_{(S, A) \coupl (T, B)}
`$
結合に関する交替法則を示すために、次のような配置を作ります。
$`\quad \begin{matrix}
f & g & \mapsto & f \coupl g \\
f' & g' & \mapsto & f'\coupl g' \\
\bar{\downarrow} & \bar{\downarrow} & & \\
f;f' & g;g' & &
\end{matrix}
`$
次に、縦横に“集計”します。
$`\quad (f;f')\coupl ( g;g')\\
\quad (f \coupl g) ; (f'\coupl g')
`$
最後に縦横集計結果が一致するかどうかをみます。
$`\quad (f; f')\coupl (g; g') \stackrel{?}{=} (f \coupl g); (f'\coupl g')`$
絵算(ストリング図の計算)でやります。
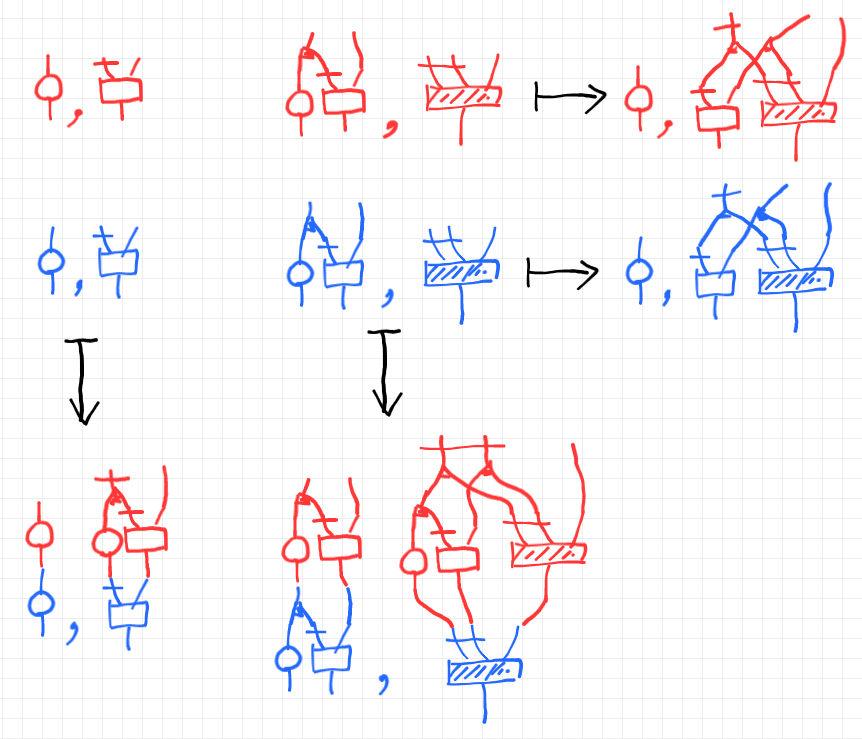
下段の $`f;f'`$ と $`g;g'`$ がカップリング可能であるためには、
$`\quad \mrm{Mix}(f;f') = \mrm{Proj}(g; g')`$
が成立している必要があります。これを確認します(以下)。状態のワイヤーを示す横棒の痕跡は気にしないでください。
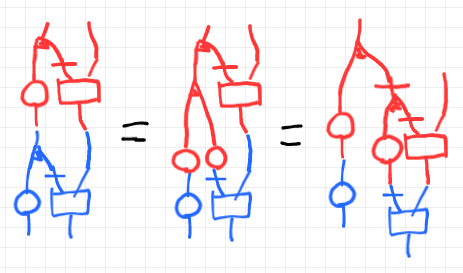
これで、$`(f;f')\coupl ( g;g')`$ が定義可能なのは大丈夫です。
問題は、縦に集計した値と横に集計した値が一致するか? です。環境付き計算ペアの第一成分〈ベースパート〉が一致するのは明らかですから、第二成分〈ファイバーバート〉に注目します。
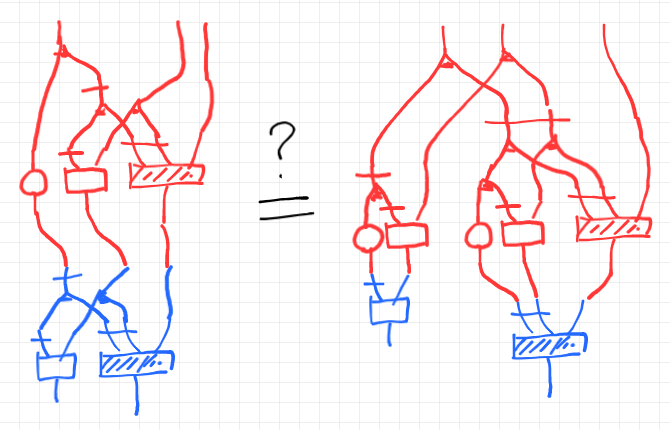
「環境付き計算と依存アクテゴリー 2/n // デカルト・ストリング図と経路行列の方法」で述べた事例は、実はこの絵等式でした。
経路行列の方法による判定は今のところ予想なので、ストリング図を“変形”して示します。
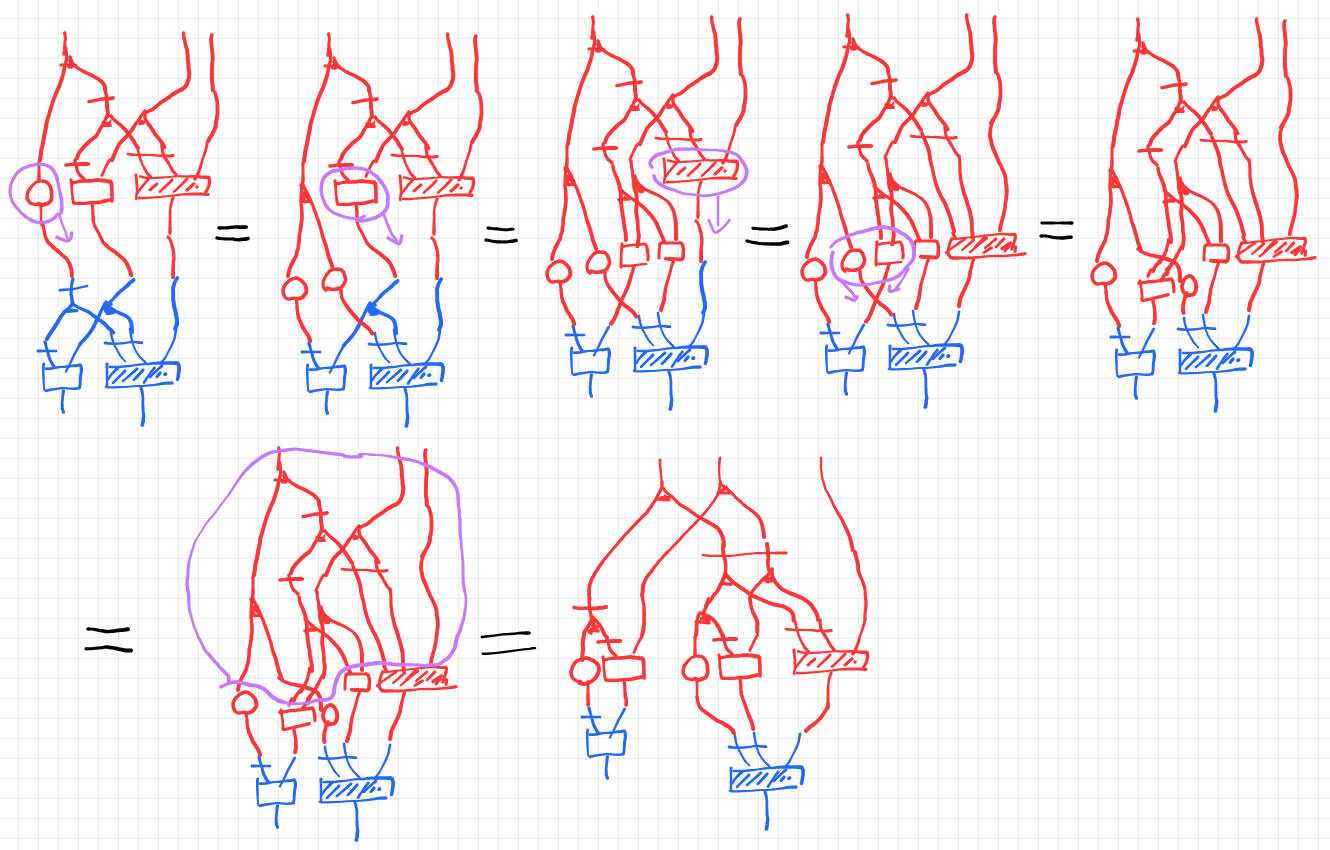
紫色の囲いの部分を“変形”の対象にします。最後の大きな紫色の囲いの部分は、デカルト圏の余可換コモノイド法則による“変形”を何度か繰り返せば“変形”できるということです。
$`\id_{(S, A)} \coupl \id_{(T, B)} = \id_{(S, A) \coupl (T, B)}`$ は次の計算で示せます。
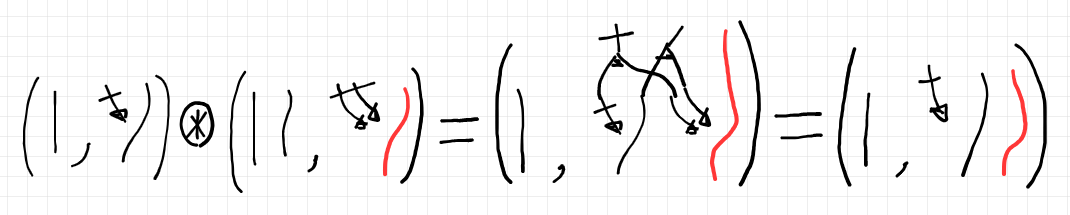
これで、カップリング演算 $`(\coupl) = \mrm{Coupl}`$ がファイバー双関手であることがハッキリしました。
はーっ、疲れた。ちょっと細切れになってしまいますが、続きは次の記事で。
- 続きは 環境付き計算と依存アクテゴリー 4/n Coming soon ([追記]それほど soon じゃないかも[/追記])
*1:記号 '$`\cong`$' は、圏同型と圏同値の両方を表しています(オーバーロード)。どちらを表すかは文脈によります。