複余有向コンテナ〈オペラッドコンテナ〉によるオペラッドの定義

アーマン／チャップマン／ウウスタル〈Danel Ahman, James Chapman, Tarmo Uustalu〉による有向コンテナは、圏と同値な構造です。コンテナをベースにした定義であることから幾つかのメリットがあります。有向コンテナの“ある種の双対”をとった余有向コンテナも同じく圏と同値になります。

余有向コンテナを少し拡張した複余有向コンテナは、オペラッド〈複圏〉と同値な構造となります。複余有向コンテナとしてオペラッドを定義しておくと、モノイド多項式モナド（「複グラフが定義するモノイド多項式関手」の最後で触れています）を定義する際などにメリットがあるでしょう。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\hyp}{\text{－} }
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\Lis}[1]{\langle {#1} \rangle}
\newcommand{\Dwn}{\downarrow }
\newcommand{\Up}{\uparrow }
% \newcommand{\Comp}{\mathop{;} }
\newcommand{\BackComp}[1]{\mathop{_{#1};} }
\newcommand{\FwdComp}[1]{ \mathop{;_{#1}} }
\newcommand{\o}[1]{\overline{#1}}
\newcommand{\O}[1]{ \,{^\triangleright \!{#1}} }
\newcommand{\whitestar}{\unicode{x2606} }
\newcommand{\vvec}[1]{\vec{\vec{#1}} }
\newcommand{\wwtilde}[1]{\widetilde{\widetilde{#1}} }
`$

内容：

有向コンテナと余有向コンテナ
圏から作る有向コンテナ／余有向コンテナ
有向コンテナ／余有向コンテナの法則
記法の約束
複余有向コンテナ
各種演算のホワイトスター
複余有向コンテナの法則
次への準備

有向コンテナと余有向コンテナ

有向コンテナ〈directed container〉に関しては、以下の過去記事に書いています。

有向コンテナの構成素を繰り返し述べます。余有向コンテナも考える都合から、過去記事で $`A`$ と書いていたファミリーを $`A^\to`$ と書きます。余有向コンテナでは $`{^\to B}`$ とします。$`\FwdComp{a}`$ と書いていた結合を $`\BackComp{a}`$ にします。$`\FwdComp{a}`$ の形は余有向コンテナで使います。

対象達の集合： $`X \in |{\bf Set}|`$
対象でインデックス付けられた集合族〈ファミリー〉： $`A^\to : X \to |{\bf Set}| \In {\bf SET}`$
射の余域を与える単項演算子（の族）： $`\Dwn_a \hyp : A^\to[a] \to X \In {\bf Set}`$
恒等射を与える定数（の族）： $`\mrm{i}_a \in A^\to[a]`$
射の結合を与える依存二項演算子（の族）： $`(\hyp_1 \,\BackComp{a} \hyp_2): A^\to[a] \times A^\to[\Dwn_a \hyp_1] \to A^\to[a] \In {\bf Set}`$

有向コンテナの詳細は「有向コンテナと多項式コモナド」をみてください。

上記の $`(\hyp_1 \,\BackComp{a} \hyp_2)`$ をカリー化した形を $`\mrm{back}_a(\hyp_1)`$ とも書きます。（back は pull-back から。）

$`\quad \mrm{back} \in \prod_{a \in X} \mrm{Map}(A^\to[a], \mrm{Map}(A^\to[\Dwn_a f], A^\to[a]) )\\
\text{For }a\in X\\
\quad \mrm{back}_a(\hyp): A^\to[a] \to\mrm{Map}(A^\to[\Dwn_a f], A^\to[a]) \In {\bf Set}\\
\text{For }f\in A^\to[a]\\
\quad \mrm{back}_a(f) : A^\to[\Dwn_a f] \to A^\to[a] \In {\bf Set}
`$

$`\mrm{back}_a(f)`$ を $`f`$ による引き戻し〈pull-back〉とも呼び、誤解の心配がなければ $`f^*`$ と略記します。また、 $`\Dwn_a f`$ を $`\mrm{cod}(f) = \mrm{cod}_a(f)`$ とも書きます。この記法で次のように書けます。

$`\quad f^* : A^\to[\mrm{cod}(f)] \to A^\to[a] \In {\bf Set}\\
\text{For }g\in A^\to[\mrm{cod}(f)]\\
\quad f^*(g) \in A^\to[a]
`$

通常の圏論の記法で書けば：

$`\text{For }c \in |\cat{C}|\\
\quad f^* : \cat{C}(\mrm{cod}(f), c) \to \cat{C}(a, c) \In {\bf Set}\\
\text{For }g\in \cat{C}(\mrm{cod}(f), c)\\
\quad f^*(g) = f; g \in \cat{C}(a, c)
`$

$`f^*`$ は、$`f`$ によるプレ結合です。

有向コンテナに双対的に、余有向コンテナ〈codirected container〉を定義します。$`A^\to[a]`$ が、対象 $`a`$ から出る射の集合であったのに対して、余有向コンテナの $`{^\to B}[c]`$ は、対象 $`c`$ に入る射の集合です。余有向コンテナも圏を定義します。

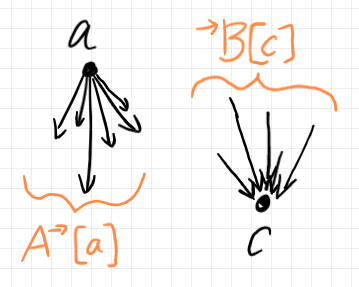
余有向コンテナの構成素は次のものです。

対象達の集合： $`X \in |{\bf Set}|`$
対象でインデックス付けられた集合族〈ファミリー〉： $`{^\to B} : X \to |{\bf Set}| \In {\bf SET}`$
射の域を与える単項演算子（の族）： $`\Up_c \hyp : {^\to B}[c] \to X \In {\bf Set}`$
恒等射を与える定数（の族）： $`\mrm{i}_c \in {^\to B}[c]`$
射の結合を与える依存二項演算子（の族）： $`(\hyp_1 \FwdComp{c} \hyp_2): {^\to B}[\Up_c \hyp_2] \times {^\to B}[c] \to {^\to B}[c] \In {\bf Set}`$

$`{^\to B}[c]`$ は、対象 $`c\in X`$ を余域〈codomain〉とする射の集合です。有向コンテナの場合と同様に、次の記法を導入します。

$`\mrm{dom}(g) = \mrm{dom}_c(g) := \,\Up_c g`$
$`\mrm{forward}_c(g) := (\hyp \FwdComp{c} g)`$

$`\mrm{forward}_c(g)`$ を $`g`$ による前送り〈push-forward〉とも呼び、誤解の心配がなければ $`g_*`$ と略記します。

通常の圏論の記法で書けば：

$`\text{For }a \in |\cat{C}|\\
\quad g_* : \cat{C}(a, \mrm{dom}(g)) \to \cat{C}(a, c) \In {\bf Set}\\
\text{For }f\in \cat{C}(a, \mrm{dom}(f))\\
\quad g_*(f) = f; g \in \cat{C}(a, c)
`$

$`g_*`$ は、$`g`$ によるポスト結合です。

有向コンテナも余有向コンテナも、圏の別定義に過ぎません。有向コンテナ／余有向コンテナの法則は、圏と同値になるように決めます。有向コンテナの法則は「有向コンテナと多項式コモナド」に書いてありますが、この記事の後の節でも再度述べます。

圏から作る有向コンテナ／余有向コンテナ

前節で使った記法は、有向コンテナを定義したアーマン／チャップマン／ウウスタル〈Danel Ahman, James Chapman, Tarmo Uustalu〉の記法をある程度は踏襲したものです。が、見慣れない記法だと戸惑うので、通常の圏論の記法をそのまま使ってもいいのではないかと思います。有向コンテナがいまいちポピュラーにならないのも、変わった記法を使っているのが一因かと思うので。

与えられた圏 $`\cat{C}`$ から有向コンテナ／余有向コンテナを作ってみて、そのとき使った記法を、いきなり（圏 $`\cat{C}`$ を前提にしないで）与えられた有向コンテナ／余有向コンテナでも使う、という方針にしましょう。

まず、ホムセットの変種を次のように定義します。

$`\quad \cat{C}^\to[a] := \{f \in \mrm{Mor}(\cat{C}) \mid \mrm{dom}(f) = a\}\\
\quad {^\to \cat{C}}[c] := \{g \in \mrm{Mor}(\cat{C}) \mid \mrm{cod}(g) = c\}
`$

$`\cat{C}^\to[a]`$ の形の集合を放出ホムセット〈outgoing homset〉、$`{^\to \cat{C}}[c]`$ の形の集合を吸入ホムセット〈incoming homset〉と呼ぶことにします。放出ホムセット／吸入ホムセットは、射の両端の片方しか指定してないので、片側ホムセット〈one-side homset〉ともいいます。

$`\mrm{dom}, \mrm{cod}`$ を、片側ホムセット上に制限した写像も、同じ名前をオーバーロードします。制限したことを明示したいなら下付き添字を使います。

$`\quad \mrm{cod}_a : \cat{C}^\to[a] \to |\cat{C}|\\
\quad \mrm{dom}_c : {^\to \cat{C}}[c] \to |\cat{C}|
`$

引き戻し $`\mrm{back}_a(f)`$ は次のように定義します。

$`\text{For }a\in |\cat{C}|\\
\text{For } f:a \to b \In \cat{C}\\
\quad \mrm{back}_a(f) : \cat{C}^\to[\mrm{cod}(f)] \to \cat{C}^\to[a]\\
\quad \mrm{back}_a(f) := \lambda\, g\in \cat{C}^\to[\mrm{cod}(f)]. f;g
`$

前送り $`\mrm{forward}_c(g)`$ は次のように定義します。

$`\text{For }c\in |\cat{C}|\\
\text{For } g:b \to c \In \cat{C}\\
\quad \mrm{forward}_c(g) : {^\to \cat{C}}[\mrm{dom}(g)] \to {^\to \cat{C}}[c]\\
\quad \mrm{forward}_c(g) := \lambda\, f\in {^\to \cat{C}}[\mrm{dom}(g)]. f;g
`$

以上のように定義すれば、次のように言えます。

$`(|\cat{C}|, \cat{C}^\to, \mrm{cod}, \mrm{id}, \mrm{back})`$ は有向コンテナとなる。
$`(|\cat{C}|, {^\to \cat{C}}, \mrm{dom}, \mrm{id}, \mrm{forward})`$ は余有向コンテナとなる。

有向コンテナ／余有向コンテナの法則

有向コンテナは5つの法則〈公理〉で規定されます。事実上圏の法則〈公理〉と同じものです。次の設定で法則を記述します。

$`\quad f\in { A^\to}[a],\; \mrm{cod}_a(f) = b\\
\quad g \in { A^\to}[b],\; \mrm{cod}_b(g) = c\\
\quad h \in { A^\to}[c],\; \mrm{cod}_c(h) = d
`$

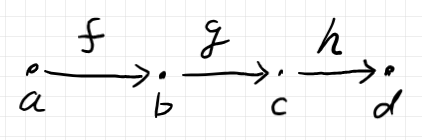
恒等の余域： $`\mrm{cod}_a(\mrm{id}_a) = a`$
結合の余域： $`\mrm{cod}_a(f \BackComp{a} g) = \mrm{cod}_{\mrm{cod}_a(f)}(g)`$
左単位法則： $`\mrm{id}_a \BackComp{a} f = f`$
右単位法則： $`f \BackComp{a} \mrm{id}_{\mrm{cod}_a(f)} = f`$
結合の結合法則： $`(f \BackComp{a} g) \BackComp{a} h = f \BackComp{a} (g \BackComp{\mrm{cod}_a(f)} h)`$

$`\mrm{back}`$ を使って書くと次のようになります。

恒等の余域： $`\mrm{cod}_a(\mrm{id}_a) = a`$
結合の余域： $`\mrm{cod}_a(\mrm{back}_a(f)(g) ) = \mrm{cod}_{\mrm{cod}_a(f)}(g)`$
左単位法則： $`\mrm{back}_a(\mrm{id}_a)(f) = f`$
右単位法則： $`\mrm{back}_a(f)(\mrm{id}_{\mrm{cod}_a(f)} ) = f`$
結合の結合法則： $`\mrm{back}_{a}( \mrm{back}_a(f)(g) )(h) = \mrm{back}_{a}(f)( \mrm{back}_{\mrm{cod}_a(f)} (g)(h) )`$

添字を省略して、$`\mrm{back}`$ を上付きアスタリスクで略記すると次のようです。見やすくなります。

恒等の余域： $`\mrm{cod}(\mrm{id}_a) = a`$
結合の余域： $`\mrm{cod}(f^*(g) ) = \mrm{cod}(g)`$
左単位法則： $`{\mrm{id}_a}^*(f) = f`$
右単位法則： $`f^*(\mrm{id}_{\mrm{cod}(f)} ) = f`$
結合の結合法則： $`( f^*(g) )^*(h) = f^*( g^* (h) )`$

結合法則の状況は以下のようです。

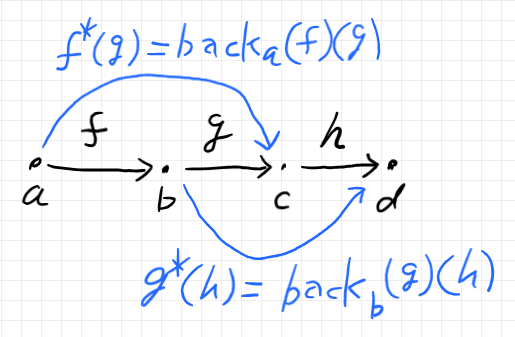
余有向コンテナの法則〈公理〉も同様です。設定も同様ですが、記述は違ってきます。

$`\quad f \in {^\to B}[b]\,\; \mrm{dom}_b(f) = a\\
\quad g \in {^\to B}[c],\; \mrm{dom}_c(g) = b\\
\quad h \in {^\to B}[d]\,\; \mrm{dom}_d(h) = c\\
`$

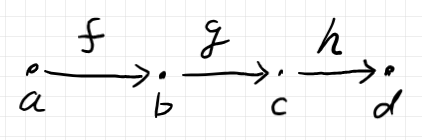
恒等の域： $`\mrm{dom}_c(\mrm{id}_c) = c`$
結合の域： $`\mrm{dom}_c(f \FwdComp{c} g) = \mrm{dom}_{\mrm{dom}_c(g)}(f)`$
左単位法則： $`\mrm{id}_{\mrm{dom}_c(g)} \FwdComp{c} g = g`$
右単位法則： $`g \FwdComp{c} \mrm{id}_c = g`$
結合の結合法則： $`(f \FwdComp{\mrm{dom}_d(h) } g) \FwdComp{d} h = f \FwdComp{d} (g \FwdComp{d} h)`$

$`\mrm{forward}`$ を使って書くと次のようになります。書き方の違いから、単位法則の左右が奇妙ですが、しょうがないです。

恒等の域： $`\mrm{dom}_c(\mrm{id}_c) = c`$
結合の域： $`\mrm{dom}_c(\mrm{forward}_c(g)(f) ) = \mrm{dom}_{\mrm{dom}_c(g)}(f)`$
左単位法則： $`\mrm{forward}_{c}(g)(\mrm{id}_{\mrm{dom}_c(g)}) = g`$
右単位法則： $`\mrm{forward}_c( \mrm{id}_c ) (g) = g`$
結合の結合法則： $`\mrm{forward}_{d}(h)( \mrm{forward}_{\mrm{dom}_d(h)}(g)(f) ) = \mrm{forward}_d( \mrm{forward}_d (h)(g) )(f)`$

添字を省略して、$`\mrm{forward}`$ を下付きアスタリスクで略記すると次のようです。

恒等の域： $`\mrm{dom}(\mrm{id}_c) = c`$
結合の域： $`\mrm{dom}(g_* (f) ) = \mrm{dom}(f)`$
左単位法則： $`g_*( \mrm{id}_{ \mrm{dom}(g) } ) = g`$
右単位法則： $`(\mrm{id}_c )_*(g) = g`$
結合の結合法則： $`h_* ( g_*(f)) = ( h_*(g) )_*(f)`$

結合法則の状況は以下のようです。

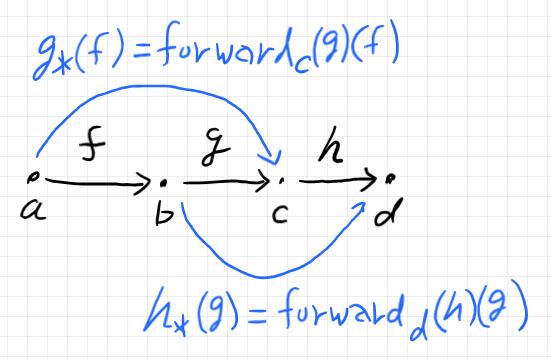
記法の約束

リストは通常 $`(a_1, \cdots, a_n)`$ のように丸括弧で囲みますが、丸括弧は他の用途でも使われて可読性が下がることがあるので、この記事では $`\vec{a} = \Lis{a_1, \cdots, a_n}`$ のように山形括弧で囲むことにします。

集合 $`X`$ のリストの集合は $`\mrm{List}(X)`$ と書き、写像 $`f:X \to Y`$ から誘導されるリストの集合のあいだの写像は $`\mrm{List}(f) : \mrm{List}(X) \to \mrm{List}(Y)`$ と書きます。$`\mrm{List}(\hyp)`$ はリスト関手ですが、リスト関手が頻出するので、次のように書きます。

$`\text{For } X\in |{\bf Set}|\\
\quad X^\star := \mrm{List}(X)\\
\text{For } f:X \to Y \In {\bf Set}\\
\quad f^\star := \mrm{List}(f)\; : X^\star \to Y^\star \In {\bf Set}`$

リストを意味する右肩の星はクリーネスター〈Kleene star〉です。アスタリスク '$`*`$' は他の用途でも使うので、目立つ黒い星 '$`\star`$' をクリーネスターに使います。

$`F`$ をファミリー〈インデックス付き集合族〉とします。

$`\quad F : X \to |{\bf Set}| \In {\bf SET}`$

ファミリーに対してもリスト関手（クリーネスター）を適用できます。

$`\quad F^\star : X^\star \to |{\bf Set}|^\star \In {\bf SET}`$

集合のリスト $`\Lis{A_1, \cdots, A_n}`$ に対して、すべての成分達の直積を作る操作を $`\prod(\hyp)`$ とします。つまり：

$`\quad \prod(\Lis{A_1, \cdots, A_n}) := A_1\times \cdots \times A_n \;\in |{\bf Set}|`$

写像 $`\prod`$ は、大きな〈小さいとは限らない〉集合のあいだの大きな写像になります。

$`\quad \prod : |{\bf Set}|^\star \to |{\bf Set}| \In {\bf SET}`$

ファミリー $`F`$ に対する $`\widetilde{F}`$ は次のように定義します。

$`\quad \widetilde{F} := \prod \circ F^\star \;: X^\star \to |{\bf Set}| \In {\bf SET}`$

$`\require{AMScd}
\quad \begin{CD}
X^\star @>{F^\star}>> |{\bf Set}|^\star \\
@| @VV{\prod}V \\
X^\star @>{\widetilde{F}}>> |{\bf Set}|
\end{CD}\\
\quad \text{commutative in }{\bf SET}
`$

具体的に書けば：

$`\text{For }\Lis{x_1, \cdots, x_n} \in X^n \subseteq X^\star \\
\quad \widetilde{F}(\Lis{x_1, \cdots, x_n}) := F(x_1)\times \cdots \times F(x_n) \;\in |{\bf Set}|`$

$`F, F^\star, \widetilde{F}`$ をオーバーロードすることもありますが、この記事では区別します。

$`\vec{f}`$ が関数〈写像〉のリスト、$`\vec{x}`$ が値のリストだとします。リストの長さが同じで、リストの項目ごとに関数適用が可能だとします。このとき次の記法を使います。

$`\quad \vec{f}\odot \vec{x} = \Lis{f_1, \cdots, f_n}\odot \Lis{x_1, \cdots, x_n}
:= \Lis{f_1(x_1), \cdots, f_n(x_n)}
`$

複余有向コンテナ

余有向コンテナの定義を少し変更して、オペラッドに対応する複余有向コンテナ〈multi-codirected container〉を定義しましょう。「オペラッドの話」の最初の2節を読んでおくといいかも知れません。

複余有向コンテナ $`M`$ は、次の構成素からなります。

対象達の集合： $`X = |M| \in |{\bf Set}|`$
対象でインデックス付けられた集合族〈ファミリー〉： $`\O{M} : X \to |{\bf Set}| \In {\bf SET}`$
複射の域（対象のリスト）を与える単項演算子（の族）： $`\mrm{arity}_c : \O{M}[c] \to X^\star \In {\bf Set}`$
恒等射を与える定数（の族）： $`\mrm{id}_c \in \O{M}[c]`$
複射のリストに対して、その前送りを与える写像（の族）： $`\mrm{forward}_c(g) : \widetilde{ \O{M}}[\mrm{arity}_c(g)] \to \O{M}[c] \In {\bf Set}`$

$`c\in X = |M|`$ に対して、$`\O{M}[c]`$ は、余域〈ターゲット〉が $`c`$ である複射〈オペレーション | 算子〉の集合です。$`\mrm{arity}`$ は $`\mrm{dom}`$（あるいは $`\mrm{src}`$）と同じですが、対象のリスト（$`X^\star`$ の要素）を値とするので名前を変えました。$`c\in X`$ と $`g \in \O{M}[c]`$ に対して、

$`\quad \mrm{arity}_c(g) \in X^\star`$

より具体的に書けば：

$`\quad \mrm{arity}_c(g) = \Lis{b_1, \cdots, b_m} \in X^m \subseteq X^\star`$

この状況を複射〈オペレーション | 算子〉のプロファイル宣言の形で書けば：

$`\quad g : \Lis{b_1, \cdots, b_m} \to c \In M`$

前送り〈push-forward〉 $`\mrm{forward}`$ について詳しく書くと：

$`\quad \mrm{forward} \in \prod_{c\in X} \prod_{g \in \O{M}[c]} \mrm{Map}(\widetilde{ \O{M}}[\mrm{arity}_c(g)], \O{M}[c]) \\
\text{For }c\in X,\; g \in \O{M}[c]\\
\quad \mrm{forward}_c(g) : \widetilde{ \O{M}}[\mrm{arity}_c(g)] \to \O{M}[c] \In {\bf Set}\\
\text{For }\vec{f} \in \widetilde{ \O{M}}[\mrm{arity}_c(g)] \\
\quad \mrm{forward}_c(g)(\vec{f}) \in \O{M}[c]
`$

$`\vec{f}`$ を具体的に書けば：

$`\quad \vec{f} = \Lis{f_1,\cdots, f_m} \in \widetilde{ \O{M}}[\mrm{arity}_c(g)]\\
\text{Let } \Lis{b_1, \cdots, b_m} := \mrm{arity}_c(g)\\
\text{Then }\\
\quad \widetilde{ \O{M}}[\mrm{arity}_c(g)] \\
= \widetilde{ \O{M}}[ \Lis{b_1, \cdots, b_m} ] \\
= \O{M}[b_1] \times \cdots \times \O{M}[b_m]\\
\text{Then }\\
\quad \vec{f} = \Lis{f_1,\cdots, f_m} \in \O{M}[b_1] \times \cdots \times \O{M}[b_m]\\
\text{i.e.} \\
\quad f_1 \in \O{M}[b_1] \\
\quad \vdots\\
\quad f_m \in \O{M}[b_m]
`$

通常のオペラッドの記法で書けば次のようなことです。

$`\quad \mrm{forward}_c(g)(\vec{f}) = \Lis{f_1,\cdots, f_m}; g = g \circ \Lis{f_1,\cdots, f_m}`$

オペラッド結合は、フル結合〈同時結合〉で与えられます。フル結合に関しては「オペラッドの話」をみてください。

余有向コンテナの場合と同様に、前送り $`\mrm{forward}_c(g)`$ を $`g_*`$ と略記します。

$`\quad g_*(\vec{f}) := \mrm{forward}_c(g)(\vec{f}) \;\in \O{M}[c]`$

フル結合の二項演算子記号 $`\FwdComp{c}`$ も使います。

$`\quad \vec{f} \FwdComp{c} g := g_*(\vec{f}) = \mrm{forward}_c(g)(\vec{f}) \;\in \O{M}[c]`$

各種演算のホワイトスター

複余有向コンテナは、$`\O{M}`$ というファミリーを台〈underlying thing〉として、その上の演算 $`\mrm{arity}, \mrm{id}, \mrm{forward}`$ から構成されます。これら3つの演算に対して、右肩にホワイトスターを乗せた演算を定義します。星の印を使っているのは、クリーネスターと関連するからです。

$`\mrm{arity}^\whitestar`$
$`\mrm{id}^\whitestar`$
$`\mrm{forward}^\whitestar`$

これらホワイトスターは、複余有向コンテナの法則を述べるときに必要となります。

演算とそのホワイトスターを順次述べていきます。まず、 $`\mrm{arity}`$ は：

$`\quad \mrm{arity} \in \prod_{c\in X} \mrm{Map}( \O{M}[c], X^\star)\\
\text{For } c \in X\\
\quad \mrm{arity}_c : \O{M}[c] \to X^\star \In {\bf Set}\\
\text{For } g \in \O{M}[c]\\
\quad \mrm{arity}_c(g) \in X^\star
`$

$`\mrm{arity}`$ のホワイトスターは：

$`\quad \mrm{arity}^\whitestar \in \prod_{\vec{b}\in X^\star} \mrm{Map}( \widetilde{\O{M}}[\vec{b}], (X^\star)^\star)\\
\text{For } \vec{b} \in X^\star\\
\quad {\mrm{arity}^\whitestar}_{\vec{b}} : \widetilde{\O{M}}[\vec{b}] \to (X^\star)^\star \In {\bf Set}\\
\text{For } \vec{f} \in \widetilde{\O{M}}[\vec{b}]\\
\quad {\mrm{arity}^\whitestar}_{\vec{b}}(\vec{f}) \in (X^\star)^\star
`$

実際の定義は：

$`\text{For } \vec{b} = \Lis{b_1, \cdots, b_m } \in X^m \subseteq X^\star\\
\text{For } \vec{f} = \Lis{f_1, \cdots, f_m} \in \O{M}[b_1] \times \cdots \times\O{M}[b_m]\\
\quad {\mrm{arity}^\whitestar}_{\vec{b}}(\vec{f}) = {\mrm{arity}^\whitestar}_{\Lis{b_1, \cdots, b_m}}(\Lis{f_1, \cdots, f_m}):= \\
\qquad \Lis{\mrm{arity}_{b_1}, \cdots, \mrm{arity}_{b_m}} \odot \Lis{f_1, \cdots, f_m} =\\
\qquad \Lis{\mrm{arity}_{b_1}(f_1), \cdots, \mrm{arity}_{b_m}(f_m)}\;\in (X^\star)^\star
`$

次に $`\mrm{id}`$ は：

$`\quad \mrm{id} \in \prod_{c\in X} \O{M}[c]\\
\text{For }c \in X\\
\quad \mrm{id}_c \in \O{M}[c]
`$

$`\mrm{id}`$ のホワイトスターは：

$`\quad \mrm{id}^\whitestar \in \prod_{\vec{b}\in X^\star} \widetilde{\O{M}}[\vec{b}]\\
\text{For }\vec{b} = \Lis{b_1, \cdots, b_m} \in X^\star\\
\quad { \mrm{id}^\whitestar}_{\vec{b}} \in \widetilde{\O{M}}[\vec{b}]
= \O{M}[b_1] \times \cdots \times \O{M}[b_m]
`$

実際の定義は：

$`\text{For }\vec{b} = \Lis{b_1, \cdots, b_m} \in X^m \subseteq X^\star\\
\quad {\mrm{id}^\whitestar}_{\vec{b}} = {\mrm{id}^\whitestar}_{\Lis{b_1, \cdots, b_m}} := \\
\qquad \Lis{\mrm{id}_{b_1}, \cdots, \mrm{id}_{b_m}} \in \O{M}[b_1]\times \cdots \times \O{M}[b_m]
`$

そして $`\mrm{forward}`$ は：

$`\quad \mrm{forward} \in \prod_{d \in X} \prod_{h \in \O{M}[d]} \mrm{Map}( \widetilde{\O{M}}[\mrm{arity}_d(h)], \O{M}[d])\\
\text{For } d \in X,\, h \in \O{M}[d]\\
\quad \mrm{forward}_d(h) : \widetilde{\O{M}}[\mrm{arity}_d(h)] \to \O{M}[d] \In {\bf Set}\\
\text{Let } \vec{c} = \Lis{c_1,\cdots, c_m} := \mrm{arity}_d(h) \;\in (X^\star)^\star\\
\text{Then }\widetilde{\O{M}}[\mrm{arity}_d(h)] = \widetilde{\O{M}}[\vec{c}] = \O{M}[c_1]\times \cdots \times \O{M}[c_m] \\
\text{For } \vec{g} = \Lis{g_1, \cdots, g_m} \in \O{M}[c_1]\times \cdots \times \O{M}[c_m]\\
\quad \mrm{forward}_d(h)(\vec{g}) = \mrm{forward}_d(h)(\Lis{g_1, \cdots, g_m}) \in \O{M}[d]
`$

リストを $`\vec{c}`$ のように表しましたが、リストのリスト（$`(X^\star)^\star`$ の要素）は $`\vvec{b}`$ のように表すことにします。

さて、$`\mrm{forward}`$ のホワイトスターですが、これは、複余有向コンテナの結合法則の記述のために使います。結合法則の状況を描いた図を先に見ておくとよいかもしれません。

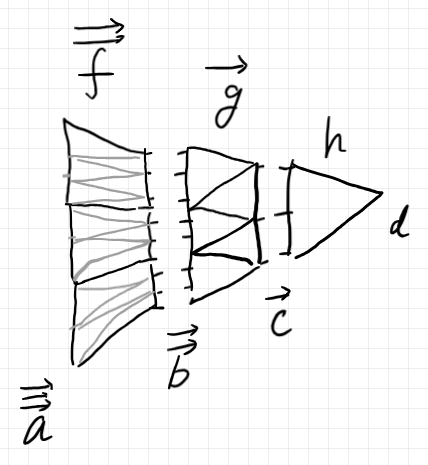
$`\quad \mrm{forward}^\whitestar \in \prod_{\vec{c} \in X^\star} \prod_{\vec{g}\in \widetilde{\O{M}}[\vec{c}] } \mrm{Map}(\wwtilde{ \O{M}}[ {\mrm{arity}^\whitestar}_{\vec{c}}(\vec{g})], \widetilde{\O{M}}[\vec{c}] ) \\
\text{For }\vec{c} = \Lis{c_1, \cdots, c_m} \in X^\star \\
\text{For }\vec{g} = \Lis{g_1,\cdots, g_m} \in \widetilde{\O{M}}[\vec{c}]
= \O{M}[c_1] \times \cdots \times \O{M}[c_m] \\
\text{Let } \vvec{b} = \Lis{\vec{b_1}, \cdots, \vec{b_m}} := {\mrm{arity}^\whitestar}_{\vec{c}}(\vec{g}) \in (X^\star)^\star\\
\text{Then }\\
\quad {\mrm{foward}^\whitestar}_{\vec{c}}(\vec{g}) :
\wwtilde{ \O{M}}[ \vvec{b} ] \to \widetilde{\O{M}}[\vec{c}] \In {\bf Set}\\
\quad \wwtilde{ \O{M}}[ \vvec{b} ] = \wwtilde{ \O{M}}[ \Lis{\vec{b_1}, \cdots \vec{b_m}} ]
= \widetilde{\O{M}}[\vec{b_1}] \times \cdots \times \widetilde{\O{M}}[\vec{b_m}]\\
\text{For }\vvec{f} = \Lis{\vec{f_1}, \cdots, \vec{f_m}} \in \widetilde{\O{M}}[\vec{b_1}] \times \cdots \times \widetilde{\O{M}}[\vec{b_m}]\\
\quad {\mrm{foward}^\whitestar}_{\vec{c}}(\vec{g})(\vvec{f}) =
{\mrm{foward}^\whitestar}_{\vec{c}}(\vec{g})(\Lis{\vec{f_1}, \cdots, \vec{f_m}})
\in \widetilde{\O{M}}[\vec{c}]
`$

実際の定義は：

$`\text{For }\vec{c} = \Lis{c_1, \cdots, c_m} \in X^\star \\
\text{For }\vec{g} = \Lis{g_1,\cdots, g_m} \in \widetilde{\O{M}}[\vec{c}]
= \O{M}[c_1]\times \cdots \times \O{M}[c_m]\\
\text{Let } \vvec{b} = \Lis{\vec{b_1}, \cdots \vec{b_m}} := {\mrm{arity}^\whitestar}_{\vec{c}}(\vec{g}) \;\in (X^\star)^\star\\
\text{For }\vvec{f} = \Lis{\vec{f_1}, \cdots, \vec{f_m}}
\in \widetilde{\O{M}}[\vec{b_1}] \times \cdots \times \widetilde{\O{M}}[\vec{b_m}]\\
\quad {\mrm{foward}^\whitestar}_{\vec{c}}(\vec{g})(\vvec{f}) =
{\mrm{foward}^\whitestar}_{\Lis{c_1, \cdots, c_m}}(\Lis{g_1, \cdots, g_m})(\Lis{\vec{f_1}, \cdots , \vec{f_m}}) := \\
\quad \Lis{ \mrm{foward}_{c_1}(g_1)(\vec{f_1}), \cdots, \mrm{foward}_{c_m}(g_m)(\vec{f_m}) }
\in \O{M}[c_1] \times \cdots \times \O{M}[c_m]
`$

複余有向コンテナの法則

複余有向コンテナの法則〈公理〉は、余有向コンテナの場合と並行に定義します。次の設定で法則を記述します。

$`\quad c \in X\\
\quad g \in \O{M}[c]\\
\text{Let } \vec{b} = \Lis{b_1, \cdots, b_m} := \mrm{arity}_c(g) \;\in X^\star\\
\quad \vec{f} \in \widetilde{\O{M}}[\vec{b}] = \O{M}[b_1]\times \cdots\times \O{M}[b_m]
`$

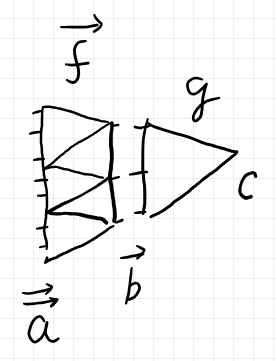
以下の $`\mrm{single}, \mrm{flatten}`$ は、リストモナドのモナド単位とモナド乗法です。

恒等の域〈アリティ〉： $`\mrm{arity}_c(\mrm{id}_c) = \mrm{single}(c) = \Lis{c}`$
結合の域〈アリティ〉： $`\mrm{arity}_c(\vec{f} \FwdComp{c} g) = \mrm{flatten}( {\mrm{arity}^\whitestar}_{\mrm{arity}_c(g)}( \vec{f} ) )`$
左単位法則： $`{\mrm{id}^\whitestar}_{\mrm{arity}_c(g)} \FwdComp{c} g = g`$
右単位法則： $`g \FwdComp{c} \mrm{id}_c = g`$
結合の結合法則：後述

恒等の域〈アリティ〉は、次のプロファイル宣言で表現できます。

$`\quad \mrm{id}_c : \Lis{c} \to c \In M`$

結合の域〈アリティ〉について考えます。$`{\mrm{arity}^\whitestar}_{\mrm{arity}_c(g)}(\vec{f})`$ を解釈しましょう。

$`\text{Let } \vec{b} = \Lis{b_1, \cdots, b_m} := \mrm{arity}_c(g) \;\in X^\star \\
\text{Let } f =\Lis{f_1, \cdots, f_m} \;\in \widetilde{\O{M}}[\vec{b}]
= \O{M}[b_1] \times \cdots \times \O{M}[b_m] \\
\quad {\mrm{arity}^\whitestar}_{\Lis{b_1, \cdots, b_m}}(\Lis{f_1, \cdots, f_m}) =\\
\qquad \Lis{\mrm{arity}_{b_1}(f_1), \cdots, \mrm{arity}_{b_m}(f_m)} \in (X^\star)^\star
`$

上記の $`{\mrm{arity}^\whitestar}_{\mrm{arity}_c(g)}(\vec{f})`$ はリストのリストですが、$`\mrm{flatten}`$ で平坦化されてリスト（$`X^\star`$ の要素）になります。平坦化されたリストが、$`\vec{f} \FwdComp{c} g = \mrm{forward}_c(g)(\vec{f})`$ のアリティを与えます。

左単位法則／右単位法則は特に難しいことはないと思います。$`\mrm{forward}`$ を使って記述しておきます。

$`\text{Let } \vec{b} = \Lis{b_1, \cdots, b_m} := \mrm{arity}_c(g) \;\in X^\star\\
\quad \mrm{forward}_c(g) ( {\mrm{id}^\whitestar}_{\vec{b}} ) =
\mrm{forward}_c(g) (\Lis{\mrm{id}_{b_1}, \cdots, \mrm{id}_{b_m} }) = g\\
\quad \mrm{forward}_c (\mrm{id}_c)(g) = g
`$

結合法則に関しては、次の設定とします。

$`\quad d\in X\\
\quad h \in \O{M}[d]\\
\text{Let }\vec{c} = \Lis{c_1, \cdots, c_m} := \mrm{arity}_d(h) \;\in X^\star\\
\quad \vec{g} = \Lis{g_1, \cdots, g_m} \in \widetilde{\O{M}}[\vec{c}]
= \O{M}[c_1]\times \cdots \times \O{M}[c_m] \\
\text{Let }\vvec{b} := \Lis{\vec{b1}, \cdots, \vec{b_m}} := {\mrm{arity}^\whitestar}_{\vec{c}}(\vec{g}) \;\in (X^\star)^\star\\
\quad \vvec{f} = \Lis{\vec{f_1}, \cdots, \vec{f_m} } \in \wwtilde{\O{M}}[\vvec{b}]
= \widetilde{\O{M}}[\vec{b_1}] \times \cdots \times \widetilde{\O{M}}[\vec{b_m}]\\
`$

この設定のもとで、複余有向コンテナの結合法則は次のように書けます。

$`\quad {\mrm{forward}^\whitestar}_{\vec{c}}(\mrm{forward}(h)(\vec{g})) (\vvec{f})
= \mrm{forward}_d (h) ( {\mrm{forward}^\whitestar}_{\vec{c}}(\vec{g})(\vvec{f}) )
`$

次への準備

複余有向コンテナは、モノイド多項式関手やモノイド多項式モナドを定義するための道具と考えています。モノイド多項式関手については次の記事に書いています。

複グラフが定義するモノイド多項式関手

今後、複余有向コンテナを道具として使っていくにあたっての注意や補足をこの節で述べます。

まず、名前。「複余有向コンテナ」は言いにくい。オペラッドと同義になる、あるいはオペラッドと対応するので、オペラッドコンテナ〈operadic container〉でいいかと思います。オペラッドコンテナがあればオペラッド（正確には、色付き非対称オペラッド）がすぐさま定義できるし、逆向きの対応も同様に容易です。

　　　複余有向コンテナ＝オペラッドコンテナ ←→ オペラッド＝複圏

オペラッドコンテナの吸入複ホムセット〈incoming multihomset〉（または吸入オペセット〈incoming opeset〉）を $`\O{M}`$ と書いてましたが、単に $`M`$ でもいいでしょう。圏 $`\cat{C}`$ とそのホムセット $`\cat{C}(\hyp, \hyp)`$ をオーバーロードするのと同様に、オペラッドコンテナ $`M`$ とその吸入オペセット $`M[\hyp]`$ はオーバーロードする、と。

オペラッドコンテナ $`M`$ は、構成素を列挙して次のように書けます。

$`\quad M = (|M|, M[\hyp], \mrm{arity}^M, \mrm{id}^M, \mrm{forward}^M)`$

$`M`$ の複射〈オペレーター〉の全体は次のように書きます（アーマン／チャップマン／ウウスタルの書き方を踏襲）。

$`\quad \overline{M} := \sum_{x \in |M|} M[x] \;\in |{\bf Set}|`$

シグマ型の標準射影は $`\mrm{trg} = \mrm{trg}^M`$ とします。

$`\quad \mrm{trg}^M : \overline{M} = \sum_{x \in |M|} M[x] \to |M| \In {\bf Set}`$

$`\mrm{arity}`$ を $`\uparrow`$ で略記するのは（これもアーマン／チャップマン／ウウスタル風）けっこう便利です。次のような記法も導入しましょう。

$`\quad \uparrow h = \,\uparrow_d h = \mrm{arity}_d(h) \in |M|^\star\\
\quad \uparrow^\whitestar \vec{g} = {\uparrow^\whitestar}_{\vec{c}} \vec{g}
= {\mrm{arity}^\whitestar}_{\vec{c}}(\vec{g}) \in (|M|^\star)^\star\\
\quad \upuparrows \vec{g} = \upuparrows_{\vec{c}} \vec{g}
= \mrm{flatten}( {\mrm{arity}^\whitestar}_{\vec{c}}(\vec{g}) ) \in |M|^\star
`$

同様にして、$`\uparrow\!\upuparrows_{\vvec{b}} \vvec{f}`$ も定義できます。上矢印の本数を丸括弧に入れた指数形式で書くことにします。

$`\uparrow^{(1)} h := \,\uparrow h`$
$`\uparrow^{(2)} \vec{g} := \,\upuparrows \vec{g}`$
$`\uparrow^{(3)} \vvec{f} := \,\uparrow\!\upuparrows \vvec{f}`$

クリーネスターの繰り返しも同じ要領で：

$`X^{\star (1)} := X^\star`$
$`X^{\star (2)} := (X^\star)^\star`$
$`X^{\star (3)} := ( (X^\star)^\star)^\star`$

ファミリー $`F:X \to |{\bf Set}|`$ に対する $`\widetilde{F}`$ の繰り返しも同様な記法を使いましょう。

$`\widetilde{F}^{(1)} := \widetilde{F} = \prod \circ F^\star`$
$`\widetilde{F}^{(2)} := \widetilde{\widetilde{F}} = \prod \circ (\widetilde{F})^\star`$
$`\widetilde{F}^{(3)} := \prod \circ (\widetilde{F}^{(2)})^\star`$

この記事では、パイ型／総積を $`\prod`$ と書きましたが、リストに沿って順番に掛け算していくときは $`\overset{\to}{\prod}`$ （「複グラフが定義するモノイド多項式関手」で使っている）がよいでしょう。対称とは限らないモノイド積〈非対称モノイド積〉$`\otimes`$ の場合でも $`\overset{\to}{\prod}`$ は定義できます。$`\cat{V} = (\cat{V}, \otimes, I)`$ は対称とは限らないモノイド圏とします。

$`\quad \overset{\to}{\prod}_{x\In \vec{a}} F(x) := F(a_1)\otimes \cdots \otimes F(a_n)
\;\in |\cat{V}|
`$

$`\overset{\to}{\prod}`$ は順番に依存した総積なので手続き的です。次のような疑似プログラムコードで書けます。

$`\quad \text{var }P : |\cat{V}|;\\
\quad P := I;\\
\quad \text{for } x \text{ in } \vec{a} \:\{\\
\qquad P := P\otimes F(x);\\
\quad \}\\
\quad \text{return }P;
`$

この記事で準備した概念・記法を用いれば、モノイド多項式関手／モノイド多項式モナドの定義と計算は楽になると思います。