カリー vs. カン、双対 vs. 随伴

去年（2023年）の年末に「カン拡張の左右： 混乱する原因がわかった！」という記事を書きました。ラムダ計算とカン拡張／カン持ち上げには類似性があるのですが、名前の対応がゆがんでいるため毎度混乱してしまう、という話でした。

この記事では、なぜラムダ計算とカン拡張／カン持ち上げが類似しているのか？ その背景を説明します。そして、ゆがんだ対応を少しでも補正するために幾つかの言葉・言い回しを導入します。また、双対と随伴の類似性も同じ背景で説明できるので、その事にも触れます。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\hyp}{\text{－} }
%\newcommand{\id}{\mathrm{id} }
\newcommand{\twoto}{\Rightarrow }
`$

内容：

二分法形容詞の件は諦める

10年以上前の2013年春に書いた記事「右カン拡張が、自然変換のラムダ計算における指数型らしい件」で、ラムダ計算と右カン拡張が似ていると書いています。2013年の記事の最初の行と最後の行だけ引用すると：

ここ2,3日、カン拡張（Kan extension）を理解しようとジタバタしてました。

...

どうも、右カン拡張は、自然変換のラムダ計算における指数型を与える仕掛けのようです。

それ以来、「似ている」という事実は知ってはいるのですが、呼び名〈名詞〉・形容詞の使い方と記法があまりにも違うので、対応で混乱してしまう事を繰り返していました。そのことは「カン拡張の左右： 混乱する原因がわかった！」に書いたとおりです。

対応が取りやすいように、ラムダ計算とカン拡張／カン持ち上げ -- 双方の呼び名・形容詞・記法に、もう少し歩み寄っていただきましょう。

ラムダ計算、特に（対称とは限らない）モノイド圏におけるラムダ計算をカリー計算〈Curry calculus〉とも呼ぶことにします*1。カン拡張／カン持ち上げに関する計算はカン計算〈Kan calculus〉と呼ぶことにします。

歩み寄っていただくとは言いながら、「カン拡張の左右： 混乱する原因がわかった！」で指摘した「左-右」の使い方の食い違いは、今更どうにもならないと思うので、そのままにします。

カリー計算〈ラムダ計算〉とカン計算とのあいだの、二分法形容詞の対応は次のようになります。

カリー	カン
正	右〈R〉
余〈Co〉	左〈L〉
左〈L〉	拡張〈Ext〉
右〈R〉	持ち上げ〈Lift〉

例えば、カリー計算におけるカリー化〈Currying〉の、カン計算における対応物をカン化〈Kanning〉（後述）と呼ぶことにして、対応表を見ながら二分法形容詞を付けていきます。

カリー	カン
正左カリー化	右拡張カン化
正右カリー化	右持ち上げカン化
余左カリー化	左拡張カン化
余右カリー化	左持ち上げカン化

形容詞「正」は通常省略するとします。呼び名は違っても、同じ記号（象形文字）を使うことにします。内容的説明は後述します。

カリー	カン	記号
左カリー化〈LCurry〉	右拡張カン化〈RExtKan〉	左肩に $`{^\wedge}`$
右カリー化〈RCurry〉	右持ち上げカン化〈RLiftKan〉	右肩に $`{^\wedge}`$
余左カリー化〈CoLCurry〉	左拡張カン化〈LExtKan〉	左下に $`{_\vee}`$
余右カリー化〈CoRCurry〉	左持ち上げカン化〈LLiftKan〉	右下に $`{_\vee}`$

'$`\cap`$' ではなくて '$`\wedge`$' を使ったのは、後で '$`\cap`$' を別な目的で使うからです。

カリー計算とカン計算の共通の抽象化

カリー計算は、（対称とは限らない）モノイド圏 $`\cat{C} = (\cat{C}, \otimes, I)`$ のなかで行います。モノイド圏の具体的な例としてはデカルト閉圏としての集合圏 $`{\bf Set} = ({\bf Set}, \times, {\bf 1})`$ があります。一方のカン計算は、小さい圏達の2-圏 $`{\bf Cat}`$ や、必ずしも小さくない圏達の2-圏 $`{\bf CAT}`$ のなかで行います。

カン計算を、$`{\bf Cat}`$ や $`{\bf CAT}`$ という具体的な2-圏ではなくて、一般的・抽象的な2-圏 $`\cat{K}`$ 内で定式化したとしましょう。それは、一般カン計算、あるいは抽象カン計算と呼べるでしょう。ところで、モノイド圏は単対象の2-圏です。となると、次の事態が予想・期待されます。

• 一般カン計算を、“モノイド圏＝単対象の2-圏”に特殊化したら、それがカリー計算

実際に、このシナリオは（だいたいは）実現できます。完全に一般的・抽象的なセッティングでのカン計算、つまりカン計算の形式論〈the formal theory of Kan calculus〉*2が出来るのか？ 既にあるのか？ 僕はよく分からない／調べてないのですが、カリー計算とカン計算の共通の抽象化の概要くらいなら説明できます。

（厳密とは限らない）2-圏 $`\cat{K}`$ に対して、次の書き方の約束をします。

• 対象〈0-射〉には、$`a, b, c`$ など、ラテン・アルファベットの最初のほうの小文字を使う。
• 射〈1-射〉には、$`f, g, k`$ など、ラテン・アルファベットの少し後の小文字を使う。
• 2-射には、$`\alpha, \beta, \eta`$ など、ギリシャ・アルファベットの小文字を使う。
• 1-射、2-射の横結合の図式順結合記号にはアスタリスク '$`*`$' を使う。
• 2-射の縦結合の図式順結合記号にはセミコロン '$`;`$' を使う。

（対称とは限らない）モノイド圏 $`\cat{C}`$ を単対象2-圏とみなして、次の書き方の約束をします。

• 唯一の0-射は、$`\star`$ と書く。
• 1-射（モノイド圏の対象）には、$`A, B, C`$ など、ラテン・アルファベットの最初のほうの大文字を使う。
• 2-射（モノイド圏の射）には、$`f, g, k`$ など、ラテン・アルファベットの少し後の小文字を使う。
• 1-射、2-射の横結合（モノイド圏のモノイド積）の記号にはオータイムス '$`\otimes`$' を使う。
• 2-射（モノイド圏の射）の縦結合の図式順結合記号にはセミコロン '$`;`$' を使う。

左カリー計算（右拡張カン計算に対応）に出現するガジェット（構造の構成素）を列挙して、それらを2-圏に移植してみましょう。2-圏側では、カン計算の用語を使います。

$`\text{モノイド圏 }\cat{C}`$	$`\text{2-圏 }\cat{K}`$
$`\text{0-射 }\star`$	$`\text{0-射 }c, d, e`$
$`\text{1-射（モノイド圏の対象） }T, A`$	$`\text{1-射 }k, f`$
$`\text{左指数1-射（モノイド圏の左指数対象） }{^T A}`$	$`\text{右カン拡張1-射 }{^k f}`$
$`\text{左評価2-射（モノイド圏の左評価射） }\mrm{lev}`$	$`\text{右拡張実行2-射 }\mrm{run}`$
$`\text{左カリー化 }{^\wedge (\hyp)}`$	$`\text{右拡張カン化 }{^\wedge (\hyp)}`$
$`\text{反左カリー化 }{_\sqcup (\hyp)}`$	$`\text{反右拡張カン化 }{_\sqcup (\hyp)}`$

単対象2-圏としてのモノイド圏では、唯一のホム圏 $`\cat{C}(\star, \star)`$ がモノイド圏の台圏となるので、通常どおり次のように書きます。

$`\quad \cat{C} := \cat{C}(\star, \star)\\
\text{For }A, B \in |\cat{C}|_1 \\
\quad \cat{C}(A, B) := \cat{C}(\star, \star)(A, B)
`$

2-圏 $`\cat{K}`$ のホム圏は次のように略記します。

$`\text{For }c, d \in |\cat{K}|_0\\
\quad [c, d] := \cat{K}(c, d)
`$

これは、$`\cat{K}`$ が内部ホム対象を持っていることを仮定しているわけではなくて、単なる略記です。$`[c, d]`$ は普通の圏（関手圏）とみなします。

左カリー計算のセッティングの概略をザッと記します。

1. モノイド圏を単対象2-圏とみなしての対象〈0-射〉 $`\star`$ が唯一ある（他の選択肢はない）。
2. モノイド圏 $`\cat{C}`$ の対象〈2-圏の1-射〉 $`T, A`$ は与えられている。
3. $`T, A`$ に対して、左指数対象〈left exponential object〉または左内部ホム対象〈left internal hom object〉と呼ばれる $`\cat{C}`$ の対象 $`{^T A} = \mrm{rhom}(T, A)`$ が定義できる。
4. $`T, A`$ に対して、左評価射〈left evaluation morphism〉と呼ばれる $`\cat{C}`$ の射〈2-圏の2-射〉 $`\mrm{lev} = \mrm{lev}_{T, A}`$ が存在する。
   $`\quad \mrm{lev} : T \otimes ({^T A}) \to A \In \cat{C}`$
5. 左カリー化〈left Currying〉と呼ばれるホムセット間の写像が存在する。
   $`\quad \mrm{LCurry}_{T, A, B} = {^\wedge (\hyp)} : \cat{C}(T\otimes B, A) \to \cat{C}(B, {^T A})\In {\bf Set}`$
6. 反左カリー化〈left unCurrying〉と呼ばれるホムセット間の写像が存在する。
   $`\quad \mrm{LUnCurry}_{T, A, B} = {_\sqcup (\hyp)} : \cat{C}(B, {^T A}) \to \cat{C}(T\otimes B, A) \In {\bf Set}`$
7. 反左カリー化は、左評価射を使って書ける。
   $`\quad {_\sqcup (\hyp)} := (T\otimes \hyp); \mrm{lev}`$
8. 左カリー化と反左カリー化は互いに逆写像である。
   $`\quad ({^\wedge (\hyp)})^{-1} = {_\sqcup (\hyp)}, \: ({_\sqcup (\hyp)})^{-1} = {^\wedge (\hyp)}`$
9. 左カリー化と反左カリー化により構成されるホムセット同型は、$`T\otimes \hyp`$（左）と $`{^T \hyp}`$（右）をペアとして含む随伴系〈adjunction | adjoint system〉を定義する。
   $`\quad \cat{C}(T\otimes B, A) \cong \cat{C}(B, {^T A}) \In {\bf Set}`$

右拡張カン計算のセッティングは以下のようです。

1. 2-圏 $`\cat{K}`$ の対象〈0-射〉 $`c, d, e`$ は与えられている。
2. 2-圏 $`\cat{K}`$ の1-射 $`k, f`$ は与えられている。
   $`\quad k: c \to d,\; f :c \to e \In \cat{K}`$
3. $`k, f`$ に対して、右カン拡張〈right Kan extension〉と呼ばれる $`\cat{K}`$ の1-射 $`{^k f} = \mrm{Ran}_k f`$ が定義できる。
   $`\quad {^k f} : d \to e \In \cat{K}`$
4. $`k, f`$ に対して、右拡張実行2-射〈right extension execution 2-morphism〉*3と呼ばれる $`\cat{K}`$ の2-射（関手圏の1-射） $`\mrm{run} = \mrm{run}_{k, f}`$ が存在する。
   $`\quad \mrm{run} :: k \ast ({^k f}) \twoto f : c \to e \In \cat{K}`$
   $`\text{i.e. } \mrm{run} : k \ast ({^k f}) \to f \In [c, e]`$
5. 右拡張カン化〈right extension Kanning〉と呼ばれるホム圏のホムセット間の写像が存在する。
   $`\quad \mrm{RExtKan}_{k, f, g} = {^\wedge (\hyp)} : [c, e](k \ast f, g) \to [d, e](f, {^k g})\In {\bf Set}`$
6. 反右拡張カン化〈right extension unKanning〉と呼ばれるホム圏のホムセット間の写像が存在する。
   $`\quad \mrm{RExtUnKan}_{k, f, g} = {_\sqcup (\hyp)} : [d, e](f, {^k g}) \to [c, e](k \ast f, g) \In {\bf Set}`$
7. 反右拡張カン化は、左実行2-射を使って書ける。
   $`\quad {_\sqcup (\hyp)} := (k \ast \hyp); \mrm{run}`$
8. 右拡張カン化と反右拡張カン化は互いに逆写像である。
   $`\quad ({^\wedge (\hyp)})^{-1} = {_\sqcup (\hyp)}, \: ({_\sqcup (\hyp)})^{-1} = {^\wedge (\hyp)}`$
9. 右拡張カン化と反右拡張カン化により構成されるホム圏のホムセットのあいだの同型は、$`k \ast \hyp`$（左）と $`{^k \hyp}`$（右）をペアとして含む随伴系〈adjunction | adjoint system〉を定義する。
   $`\quad [c, e](k\ast g, f) \cong [d, e](g, {^k f}) \In {\bf Set}`$

左カリー計算の随伴系（すぐ下）と右拡張カン計算の随伴系を図示すると次のようになります。

$`\qquad\xymatrix@C+2.5pc{
\cat{C} \ar@/^1.5pc/[r]_{T\otimes \hyp} \ar@{}[r]|{\bot}
& \cat{C} \ar@/^1.5pc/[l]_{^T \hyp}
}\\
\quad \cat{C}(T\otimes B, A) \cong \cat{C}(B, {^T A}) \In {\bf Set}\\
`$

右拡張カン計算の随伴系：

$`\qquad\xymatrix@C+2.5pc{
[c, e] \ar@/^1.5pc/[r]_{k \ast \hyp} \ar@{}[r]|{\bot}
& [d, e] \ar@/^1.5pc/[l]_{^k \hyp}
}\\
\quad [c, e](k\ast g, f) \cong [d, e](g, {^k f}) \In {\bf Set}
`$

$`\cat{C}`$ を $`\cat{C}(\star, \star)`$ に、$`[c, e]`$ を $`\cat{K}(c, e)`$ に戻して書けば、より類似性が際立つでしょう。$`\cat{K}`$ を $`{\bf Cat}`$ と置いた場合は次のようです。

$`\qquad\xymatrix@C+2.5pc{
[\cat{C}, \cat{E}] \ar@/^1.5pc/[r]_{K \ast \hyp} \ar@{}[r]|{\bot}
& [\cat{D}, \cat{E}] \ar@/^1.5pc/[l]_{^K \hyp}
}\\
\quad [\cat{C}, \cat{E}](K \ast G, F) \cong [\cat{D}, \cat{E}](G, {^K F}) \In {\bf Set}
`$

つまり、次のような事になっています。

• 一般カン計算を、“モノイド圏＝単対象の2-圏”に特殊化したら、それがカリー計算
• 一般カン計算を、具体的な2-圏 $`{\bf Cat}`$（または $`{\bf CAT}`$）上で考えたら、それが関手圏のカン計算

双対と随伴の共通の抽象化

随伴系〈adjunction | adjoint system〉については、次の過去記事で書いています。

• 代数的な随伴系から自然なホムセット同型へ
• 随伴の自然なホムセット同型から単位自然変換へ

また、指標／ペースティング図／ストリング図による随伴系の記述が次の過去記事にあります。

• 随伴系の2-指標

前節と同様に、双対と随伴の共通の抽象化を2-圏 $`\cat{K}`$ のなかで定式化します。$`\cat{K}`$ の2つの1-射 $`f, g`$ が随伴ペアであることを次のように書きます。

$`\quad f \dashv g`$

これだけでは情報が不足なので、次のように書くことにします。

$`\quad (f: c \to d) \dashv (g: d \to c)\text{ by } \eta, \varepsilon \In \cat{K}\\
\qquad\xymatrix@C+2.5pc{
c \ar@/^1.5pc/[r]_{f} \ar@{}[r]|{\bot}
& d \ar@/^1.5pc/[l]_{g}
}`$

2-射 $`\eta, \varepsilon`$ が随伴系の中核的構成素です。$`\eta`$ を随伴系の単位〈unit〉、$`\varepsilon`$ を余単位〈counit〉と呼びます。次のような“象形文字”で表すことにします。

$`\quad \eta = {_f \eta_g} = {_f \cap _g} :: \mrm{id}_c \twoto f*g : c \to c \In \cat{K}\\
\quad \varepsilon = {_g \varepsilon_f} = {_g \cup _f} :: g*f \twoto \mrm{id}_d : d \to d \In \cat{K}
`$

次のストリング図を見れば、“象形文字”の意味が分かるでしょう。ただし、象形文字や「上下左右」の形容詞は描画方向に影響されます。ここでの描画方向は、縦結合が上から下、横結合が左から右です。

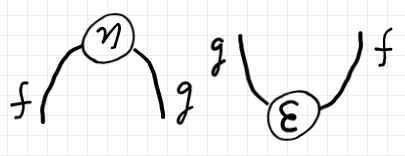
随伴系が満たすべき法則はニョロニョロ法則〈snake {law | relation | equation | identity}〉です。象形文字を使って書くと次のようです。

$`\quad ({_f \cap _g} * \mrm{I}_f) ; (\mrm{I}_f * {^g \cup ^f}) = \mrm{I}_f \In \cat{K}\\
\quad (\mrm{I}_g * {_f \cap _g} ) ; ({^g \cup ^f} * \mrm{I}_g) = \mrm{I}_g \In \cat{K}
`$

絵で描けば：

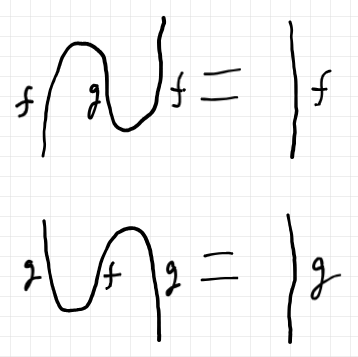
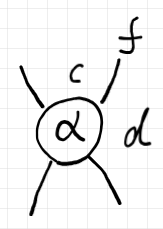
2-射 $`\alpha`$ を次のようだとします。

$`\quad \alpha :: \_ * f \twoto \_ *\_ : \_ \to d \In \cat{K}`$

ここで、アンダースコアのところは don't care 、何でもいいということです。絵で描けば次のようです。

4本の脚の一部が恒等射でもかまいません。例えば、左上と右下が恒等射なら次のようです。

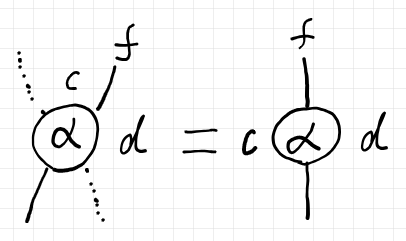
$`\alpha`$ に $`{_f \cap _g}`$ を結合する操作をひとつのオペレータ〈コンビネータ〉と考えると次のようになります。

$`\quad \cat{K}(\_, d)(\_ * f ,\, \_ *\_) \ni \alpha \mapsto (\mrm{I} * {_f \cap _g}) ; (\alpha * \mrm{I}_g) \in \cat{K}(\_, c)(\_ ,\; \_ *\_ * g)`$

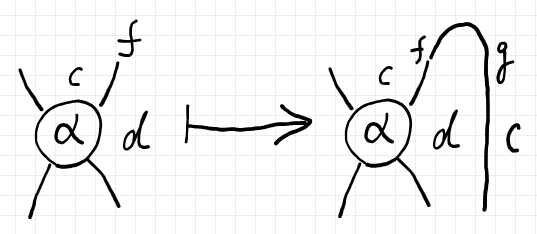
これを、次のように略記します。

$`\quad \alpha \mapsto \alpha^\cap`$

$`\cup`$ を結合する操作も同様な略記 $`\beta_\cup`$ を使うと次が成立します。

$`\quad {\alpha^\cap}_\cup = (\alpha^\cap)_\cup = \alpha`$

$`{_\cup \alpha^\cap}`$ や $`{^\cap \alpha _\cup}`$ を作ることもできます。これは $`\alpha`$ のメイト〈mate〉と呼びます。

2-圏における一般論はこのくらいにして、特別な2-圏（単対象2-圏）であるモノイド圏に特殊化してみましょう。

$`A, B`$ をモノイド圏の対象（2-圏の1-射）とします。$`A, B`$ が随伴ペアであるとき、双対ペア〈dual pair〉とも呼びますが、記法は同じにします。

$`\quad A \dashv B`$

詳しく書けば：

$`\quad A \dashv B \text{ by }\mrm{coev}, \mrm{ev} \In \cat{C}`$

単位に相当する $`\mrm{coev}`$ を双対系の余評価射〈coevaluation morphism〉、余単位に相当する $`\mrm{ev}`$ を評価射〈evaluation morphism〉と呼びます（「単位」、「余単位」という呼び名も使います）。やはり象形文字で表します。

$`\quad \mrm{coev} = {_A\mrm{coev}_B} = {_A \cap _B} : I \to A\otimes B \In \cat{C}\\
\quad \mrm{ev} = {^B\mrm{ev}^A} = {^B \cup ^A} : B\otimes A \to I \In \cat{C}
`$

ニョロニョロ法則は次のようになります．

$`\quad ({_A \cap _B} \otimes \mrm{id}_A); (\mrm{id}_A \otimes {^B \cup ^A}) = \mrm{id}_A\\
\quad (\mrm{id}_B \otimes {_A \cap _B}) ; ({^B \cup ^A}) \otimes \mrm{id}_B) = \mrm{id}_B
`$

$`f`$ のメイト $`{_\cup f^\cap}`$ は双対射〈dual morphism〉になります。

具体的な2-圏である $`{\bf Cat}`$ や $`{\bf CAT}`$ で同様な議論をすれば、それは関手の随伴ペアの話になります。

おわりに

2-圏のなかで一般論〈抽象論 | 形式論〉を準備しておいて、それを単対象の2-圏であるモノイド圏に適用してみる、あるいは具体的な2-圏である $`{\bf Cat}, {\bf CAT}`$ に適用してみる方法は、類似性のある概念（例えば左カリー計算と右拡張カン計算）をまとめて扱うときに便利です。

概念的に類似性があっても、用語法や記法はまったく違っている場合があり、そこはネックになります。適度に歩み寄っていただくしかないですね。

*1:ラムダ計算といえば、カリーよりチャーチ〈Alonzo Church〉を挙げるべきです。が、「カリー化」がポピュラーな言葉なので、それから「カリー」を拝借しているだけで、歴史的事実に基づいて命名しているわけではないです。

*2:The formal theory of XXX は一種のテンプレートで、起源はおそらく、ストリート〈Ross Street〉の The formal theory of monads (July 1972) でしょう。

*3:実行〈execution〉に特別な意味はなくて、ダジャレで付けた run からの連想に過ぎません。「右カン拡張の eval は run」参照。run は「右カン拡張が、自然変換のラムダ計算における指数型らしい件」から使っています。前例があったような気がします。