モノイド圏があると、それから複圏と多圏が作れます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\Lis}[1]{\langle {#1} \rangle}
\newcommand{\MComp}[1]{ \mathop{;_{#1}} }
\newcommand{\PComp}[2]{ \mathop{_{#1};_{#2}} }
`$
内容:
モノイド圏
モノイド圏〈monoidal category〉は、圏にモノイド積〈monoidal product〉と単位対象〈unit object〉が載った構造です。モノイド圏を、記号の乱用で次のように書きます。
$`\quad \cat{C} = (\cat{C}, \otimes, I)`$
右辺に現れる $`\cat{C}`$ は台圏〈underlying category〉、$`\otimes`$ はモノイド積、$`I`$ は単位対象です。モノイド積は、対象・射に対する掛け算で、単位対象(と単位対象の恒等射)が掛け算の単位元のようなものです。モノイドと同様な法則が成立しますが、完全な等式としての法則は期待できず、弱い意味の等式(同型)になります。が、今は、法則の弱さは気にしないことにします。
モノイド圏の例を幾つか挙げます。
- 集合圏: 対象は集合、射は写像〈関数〉、対象のモノイド積は集合の直積、射のモノイド積は写像の直積、単位対象は単元集合。
- 自然数足し算: 対象は自然数、射は大小順序、対象のモノイド積は足し算、射のモノイド積は和の大小順序、単位対象はゼロ。
- 自然数掛け算: 対象は自然数、射は約数倍数順序、対象のモノイド積は掛け算、射のモノイド積は積の約数倍数順序、単位対象はイチ。
- 行列圏: 対象は自然数、射は行列、対象のモノイド積は足し算、射のモノイド積は対角ブロック和、単位対象はゼロ。
- 関係圏直和: 対象は集合、射は関係(直積の部分集合)、対象のモノイド積は集合の直和、射のモノイド積は関係の直和(部分集合の直和)、単位対象は空集合。
- 関係圏直積: 対象は集合、射は関係(直積の部分集合)、対象のモノイド積は集合の直積、射のモノイド積は関係の直積(部分集合の直積)、単位対象は単元集合。
- 実係数有限次元ベクトル空間の圏: 対象はベクトル空間、射は線形写像、対象のモノイド積はベクトル空間のテンソル積、射のモノイド積は線形写像のテンソル積、単位対象は(1次元ベクトル空間としての)実数体。
以上の例に挙げた圏は、モノイド積 $`A\otimes B`$ と $`B\otimes A`$ のあいだの同型が系統的に与えられる、という意味で対称モノイド圏です。対称性を持たないモノイド圏をひとつだけ挙げておくと:
- 自己関手圏: 対象は圏 $`\cat{C}`$ の自己関手、射は自己関手のあいだの自然変換、対象のモノイド積は自己関手の結合、射のモノイド積は自然変換の横結合、単位対象は恒等自己関手。
以下の節で、複圏の構成には対称性は仮定しませんが、多圏の構成では対称性を仮定します。
複圏
以下で使う複圏/多圏に対する用語法の方針は、「コンフリクト回避より整合性を優先する」です。以下の過去記事も参照。
複圏〈multicategory〉(非対称色付きオペラッド〈non-symmetric colored operad〉とも呼ぶ)とは、圏類似代数系で、射(複射〈multimorphism〉と呼ぶが)の域が、対象のリストで与えられるものです。
$`\cat{M}`$ が複圏のとき、$`|\cat{M}|`$ を $`\cat{M}`$ の対象の集合(小さい集合とは限らない)、$`\mrm{List}(|\cat{M}|)`$ を対象のリストの集合とします。対象のリストは、
$`\quad \vec{A} = \Lis{A_1, \cdots, A_n}\; \in \mrm{List}(|\cat{M}|)\\
\quad \text{i.e. }A_1 \in |\cat{M}|, \cdots, A_n\in |\cat{M}|`$
のように書くとします。山形括弧を使ったのは、丸括弧が多用され過ぎて視認性・可読性が悪くなるからです。それ以外の意図〈他意〉はありません。
$`\vec{A} \in \mrm{List}(|\cat{M}|),\, B\in |\cat{M}|`$ に対して、複圏の複ホムセット〈multi-homset〉を次のように書きます。
$`\quad \cat{M}(\vec{A}, B) = \cat{M}(\Lis{A_1, \cdots, A_n}, B) \; \in |{\bf Set}|`$
上記複ホムセットは、プロファイルが $`\vec{A} \to B`$ である $`\cat{M}`$ の複射達からなる集合です。以下は同値です。
- $`f \in \cat{M}(\vec{A}, B) = \cat{M}(\Lis{A_1, \cdots, A_n}, B)`$
- $`f : \vec{A} \to B \In \cat{M}`$
- $`f : \Lis{A_1, \cdots, A_n} \to B \In \cat{M}`$
圏と同様に、複圏でも対象ごとの恒等複射〈identity multimorphism〉 $`\mrm{id}_A`$ があります。複射と複射(あるいは複射のリスト)のあいだの複結合〈multicomposition〉〈オペラッド結合〈operadic composition〉〉が定義されています。
複圏の複結合には、単純な複結合〈部分結合 | ナロー結合 | マークル〈Markl〉結合〉とフル複結合〈トータル結合 | ワイド結合〉があります。複射 $`f`$ を、複射 $`g`$ の $`i`$ 番目の入力位置に(単純に)複結合すること(複結合した結果)を
$`\quad f\MComp{i} g`$
と書くことにします。
より詳しいことは、以下の過去記事を参照してください。
モノイド圏から作る複圏
$`(\cat{C},\otimes, I )`$ をモノイド圏とします。モノイド圏から作られた複圏 $`\cat{M} := \mrm{Multi}(\cat{C})`$ とは、次のような複圏です。
- 対象の集合: $`|\cat{M}| = |\cat{C}|`$
- 複ホムセット: $`\cat{M}(\Lis{A_1, \cdots, A_n}, B) := \cat{C}(A_1 \otimes \cdots \otimes A_n, B)`$ 、特に $`\cat{M}(\Lis{}, B) := \cat{C}(I, B)`$
- 恒等複射: $`\mrm{id}_A:= (\mrm{id}_A \text{ as multimorphism} )`$
- 単純な複結合: $`f\MComp{i} g := ( (\mrm{id}_{A_1}\otimes \cdots\otimes f\otimes \cdots\otimes\mrm{id}_{A_n})\,; g \text{ as multimorphism})`$
単純な複結合の定義は、$`i`$ 番目以外の入力位置には恒等射を繋ぐ、ということです。ストリング図を描くと事情がハッキリするでしょう。
このようにして作られた $`\cat{M} = \mrm{Multi}(\cat{C})`$ は、実際に複圏の公理を満たすことが示せます(思いのほか面倒ですが)。$`\mrm{Multi}(\cat{C})`$ の複射は、実体としては $`\cat{C}`$ の射です。しかし、プロファイル(見かけ上の肩書き)が変わることで、扱いが変わってきます。複ホムセットとホムセットは同一の集合ですが、だからといって「どっちでも同じ」というわけではありません。
集合圏 $`{\bf Set}`$ から作られる $`\mrm{Mult}({\bf Set})`$ の複射は、複関数(多変数関数、多引数関数 | multifunction)です。$`{\bf Set}`$ の射と $`\mrm{Mult}({\bf Set})`$ の複射を区別することは、タプル1引数の関数と多引数関数を区別することです。場面によっては、「どっちでも同じ」というわけではありませんから区別する必要があります。以下の記事が参考になるかも知れません。
最初の節に挙げたモノイド圏の例から、実際に複圏を作ってみるといいでしょう。
モノイド圏から作る多圏
圏の射は 1-in 1-out の“関数のようなモノ”であり、複圏の複射は n-in 1-out の“多変数関数のようなモノ”でした。多圏の多射は n-in m-out の“多変数多戻り値関数のようなモノ”を抽象化した概念です。
多圏〈polycategory〉 $`\cat{P}`$ は、次のような構成素を持ちます。
- 対象の集合: $`|\cat{P}|`$
- 多ホムセット〈poly-homset〉: $`\vec{A}, \vec{B} \in\mrm{List}(|\cat{P}|)`$ に対して $`\cat{P}(\vec{A},\vec{B}) \;\in |{\bf Set}|`$ 、プロファイルが $`\vec{A} \to\vec{B}`$ である多射〈polymorphism〉の集合
- 恒等多射〈identity polymorphism〉: $`\mrm{id}_A : \Lis{A}\to \Lis{A} \In \cat{P}`$
- 単純な多結合〈polycomposition〉: 2つの多射 $`f, g`$ が結合可能性の条件を満たすとき、$`f\PComp{i}{j} g`$ は、$`f`$ の $`i`$ 番目の出力を、$`g`$ の $`j`$ 番目の入力に繋いで作った多射
より詳しいことは、以下の過去記事を参照してください。
モノイド圏から多圏を構成する場合は、対称性がないとキビシイので対称性を仮定します。ストリング図で見ると、対称性があるとは、ワイヤーの交差ができることです。$`A, B`$ の交差を与える射を $`\sigma_{A, B}`$ と書きます。
$`(\cat{C},\otimes, I, \sigma )`$ を対称モノイド圏とします。対称モノイド圏から作られた多圏 $`\cat{P} := \mrm{Poly}(\cat{C})`$ とは、次のような多圏です。
- 対象の集合: $`|\cat{P}| = |\cat{C}|`$
- 多ホムセット: $`\cat{P}(\Lis{A_1, \cdots, A_n}, \Lis{B_1, \cdots, B_m}) := \cat{C}(A_1 \otimes \cdots \otimes A_n, B_1\otimes \cdots \otimes B_m)`$ 、空リスト $`\Lis{}`$ は単位対象 $`I`$ に対応させる。
- 恒等多射: $`\mrm{id}_A:= (\mrm{id}_A \text{ as polymorphism} )`$
- 単純な多結合: $`f\PComp{i}{j} g`$ 一般的には複雑、下に絵と例を示す。
下図は、$`f`$ が 2-in 3-out で、$`g`$ が 4-in 2-out の場合の $`f \PComp{2}{3} g`$ を表すストリング図です。多結合で“余った”ワイヤーを処理するためにワイヤー交差、つまりモノイド圏の対称性が必要となります。
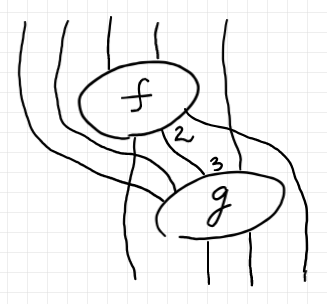
このようにして作られた $`\cat{P} = \mrm{Poly}(\cat{C})`$ は、実際に多圏の公理を満たすことが示せます(これも面倒ですが)。$`\mrm{Poly}(\cat{C})`$ の多射を、$`\cat{C}`$ の射と同一視していいとは限らないのは複圏の場合と同様です。
最初の節に挙げた対称モノイド圏の例から、実際に多圏を作ってみるといいでしょう。