「ストリング図とハイパーグラフ図」でハイパーグラフ図を紹介しました。その記事で、次のように書きました。
ハイパーグラフ図は、ストリング図とかなり似ているので、僕は積極的にハイパーグラフ図を使うことはなかったのですが、...[snip]...
僕がハイパーグラフ図を使わなかった理由は、メリットよりもデメリットのほうが目立つからです。それらのデメリットは、ハイパーグラフ図を使う上での注意事項となります。$`\require{color}
\newcommand{\orange}[1]{\textcolor{orange}{#1}}
\newcommand{\red}[1]{\textcolor{red}{#1}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\mrm}[1]{\mathrm{#1}}
%`$
内容:
ストリング図の特徴: 比較のために
ハイパーグラフ図のメリット/デメリットをストリング図と比較して議論することにします。そのためにまず、ストリング図の特徴を再確認しておきます。
狭義のストリング図は2次元のキャンバスに描かれます。広義のストリング図(サーフェイス図も含む)は任意次元のキャンバスに描かれます。ここでは2次元キャンバスに描かれるストリング図を考えます。
ストリング図では、キャンバスの横方向/縦方向に前もって意味を定めています。僕が通常使っている描き方だと:
- 横方向は左から右、モノイド積〈monoidal product〉の方向とする。
- 縦方向は上から下、結合〈composition〉の方向とする。
方向の意味は約束さえすればよく、どう約束するかは自由です(約束が人によりバラバラなことは「絵算(ストリング図)における池袋駅問題の真相」参照)。方向/向きを前もって約束しているので、ワイヤーに矢印を描くことはしません(してもかまわないけど)。
ストリング図を構成する面〈エリア〉、線〈ワイヤー〉、点〈ノード〉は、重ねたり交差させたりすることは禁止されています。キャンバスの一点は、ストリング図のどれかひとつ(そしてただひとつ)の面・線・点に所属します。
ストリング図は約束ごとや禁止事項があるので、描画の自由度は制限されます。ペースティング図やハイパーグラフ図はもっと自由にレイアウトできます。しかし、ストリング図は制約が強いことにより、構造が把握しやすく、テキストへの翻訳も容易になります。
次は、確率の計算でよく出てくるストリング図です(マルコフ核 $`f`$ の分布 $`p`$ による同時化)。結合の方向を上から下、モノイド積の方向を左から右として描いています。
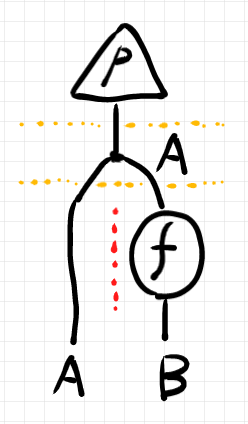
オレンジ色の横線でスライスして、各スライスをテキスト化して結合〈compose〉するとテキストの式が得られます。赤い縦線はモノイド積になります。
$`\quad p\orange{\,;}\Delta_A\orange{\,;}( \id_A \red{\otimes} f )\\
\text{where}\\
\quad p:I \to A\\
\quad \Delta_A:A \to A\otimes A\\
\quad \id_A:A \to A\\
\quad f:A \to B`$
レイアウトの自由さ
「ストリング図とハイパーグラフ図」において、次の左右のハイパーグラフ図は同じだと言いました。
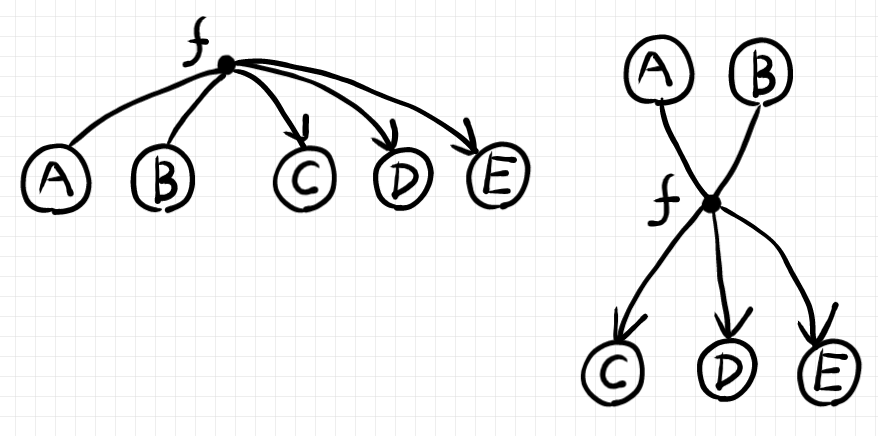
上の左側の図の $`A, B`$ を時計回りに持ち上げると、$`B,A`$ になってしまうように思えます。実際に、180度回転してみると次の図になります。
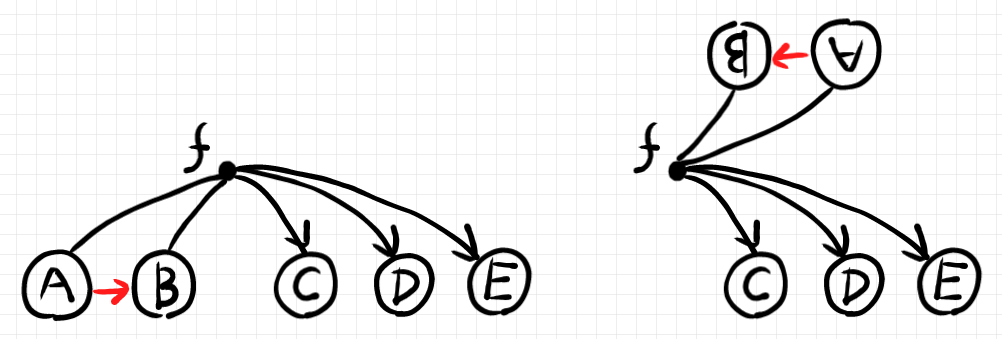
右側の図において、$`B`$ が上の左側、$`A`$ が上の右側に来て逆転しています。が、もともと下にあった$`A, B`$ はリスト $`(A, B)`$ でした。$`A`$ が一番目で、$`B`$ が二番目という順番があります。赤い矢印は順番の矢印です。時計回り180度回転で、右が一番目で左が二番目になっているので、右側の図の上側は相変わらずリスト $`(A, B)`$ (ただし、右から左に読む)なのです。見た目が違っても内容的に同じです。
とはいえ、これってややこしくないですか? 描画方向を固定せずに自由なレイアウトを許すと、こういうややこしいことが頻繁に起こります。レイアウトの自由さゆえに、見た目が違っても内容的に同じ図がたくさんたくさん出現します。
違った見た目の図が内容的に同じかどうかを判断するのはかなり難しいことです。レイアウトの自由さと引き換えに、視認性(視覚的な可読性)が犠牲になることは注意すべきです。
分岐や合流が不明瞭
先に出したストリング図を、忠実にハイパーグラフ図に直せば次のようになります。
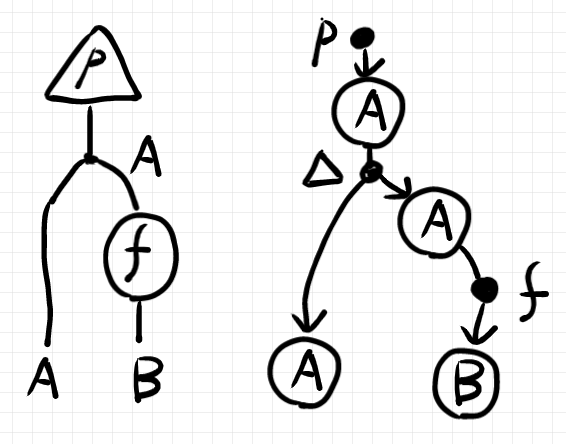
ストリング図の分岐ノード(意味はコピー射)もハイパー辺として描くべきです。ところが、しばしば $`p`$ と分岐ノードを合わせた $`p;\Delta_A`$ が単一のハイパー辺にまとめられてしまいます。下の右側の図がまとめてしまった図の一例です。まとめ方(略記の描き方)は約束次第なので色々あります。
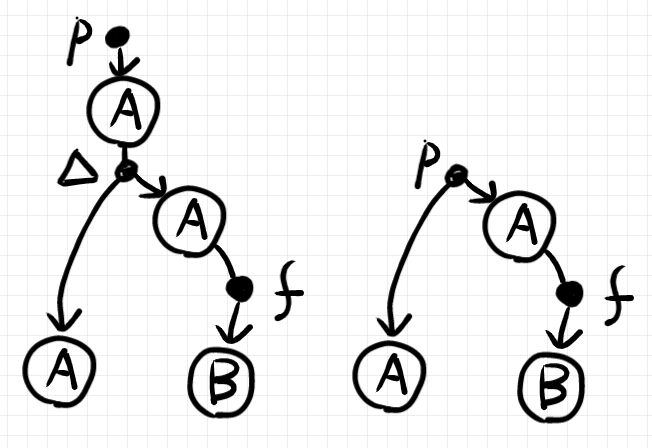
レイアウトは自由なので、下の右側のように描いてもかまいません。
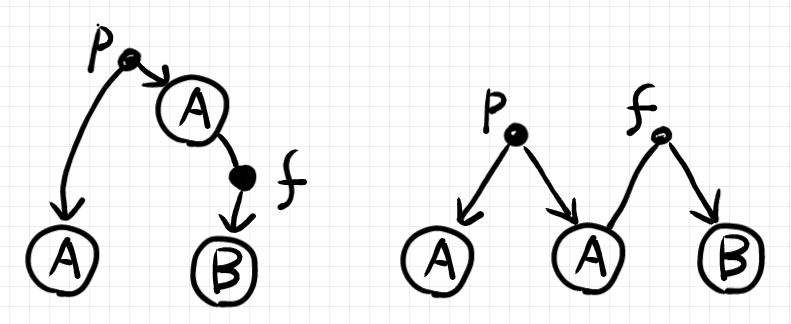
ストリング図に比べると、モノイド圏の射としての構造は読み取りにくいですね。略記やレイアウトの変更は、たいてい難読化に繋がります。
ワイヤリング変形がうまくいかない
下の図は、コンパクト閉圏におけるベータ変換〈ベータ{簡約 | 還元}〉をストリング図で描いたものです。
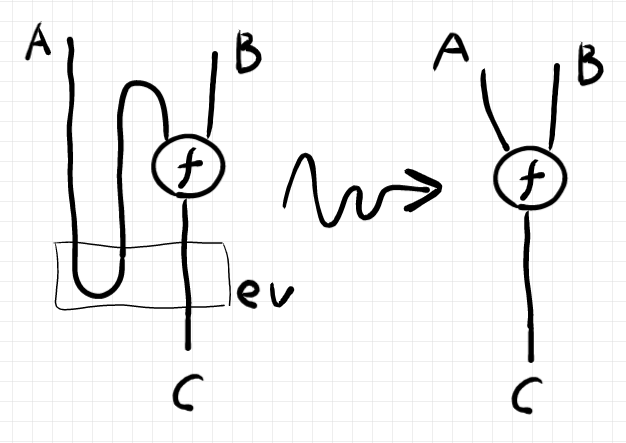
象形文字を使ったテキストで表すなら次のようです。
$`\quad ( (\id_A \otimes\, {^\cap f}); \mrm{ev}: A\otimes B \to C) \leadsto
(f:A\otimes B \to C)\\
\text{where}\\
\quad \id_A : A \to A\\
\quad {^\cap f} : B \to A^*\otimes C\\
\quad \mrm{ev} = \mrm{ev}_{A,C}:A\otimes (A^* \otimes C) \to C\\
\quad {^\cap f} := (\cap_A \otimes \id_B);(\id_{A^*} \otimes f)\\
\quad \mrm{ev} = \mrm{ev}_{A,C} := \cup_A \otimes \id_C\\
\quad \cap_A : I \to A^*\otimes A\\
\quad \cup_A : A\otimes A^* \to I`$
ベータ変換は、ニョロニョロ・ワイヤーの引き伸ばしとして自然に解釈できますし、テキスト表示との関係も素直に理解できます。
一方、ハイパーグラフ図で同じベータ変換を描くと次のようです。
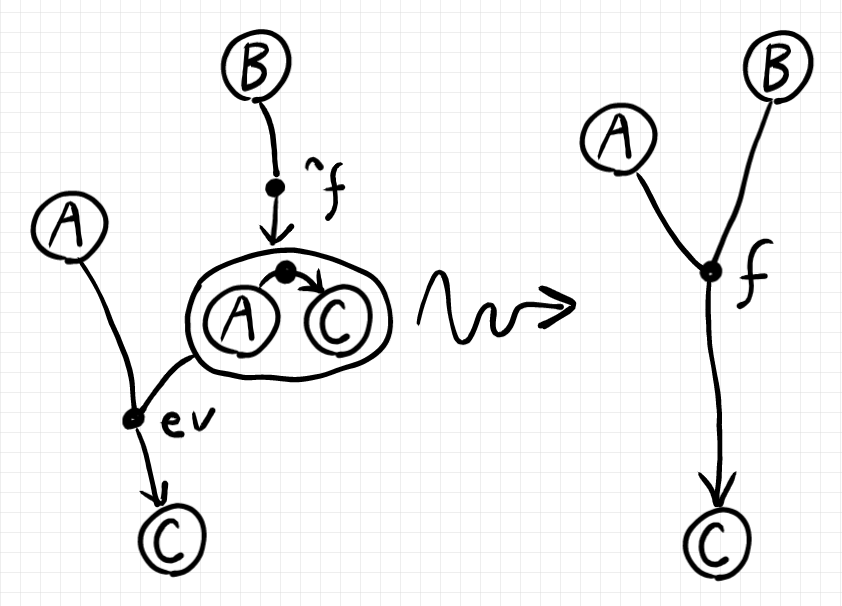
ストリング図ほどの自然さ/素直さは感じられません。
ハイパーグラフ図を使うときは、この記事で述べたような問題点に注意する必要があります。あるいは、ハイパーグラフ図は使わずにやっぱりストリング図にするという判断もあり得ます。