このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

バタニンの球複体 とりあえず導入

雑記／備忘

12日・日曜の圏論勉強会二次会で、バエズの負次元圏を「5分で説明できる」と言っておきながら、混乱して全然説明できなかったよー。で、もとの資料（http://arxiv.org/abs/math/0608420 のP.10からP.13）を読み返していちおう確認しました。

バエズの負次元圏のことは、この注釈で言及しているし、メモ編にも書いてあります。でも、ある程度は系統的に話すと「5分」では無理かもしれないなー。それで説明の方法を考えてみました。高次元の図形を導入するのは避けられないので、バタニンの方法（globular approach）の簡略版を導入しておきます*1。

内容：

n-圏がめんどくさいのは結合がたくさんあるから

折に触れてn-圏のハナシはしています。時間順にリストしてみると：

普通の圏（1-圏）の理解のためにも、n-圏は知っておいた方がいいな、と僕は思うのですが、そうは言ってもn-圏はやっぱり難しいです。n = 2 くらいなら普通の圏の延長と考えてなんとかなりますが、n = 3 だとだいぶ面倒、n = 4 以上だと手計算はほぼ絶望的。そもそも計算法則を書き下すにもエライ騒ぎです（例→ http://math.ucr.edu/home/baez/trimble/tetracategories.html）。

やたらにめんどくさくなるのは、結合演算（composition；合成）がたくさんあるせいです。計算法則もイッパイ出てきて、さらに弱いn-圏（weak n-category）だと、計算法則の合理性を主張するメタ法則もあったりします。結合演算を忘れてしまえばかなり簡単になります。それで、n-圏から結合演算を忘れた構造を取り扱うことにします。

そんなもの扱ってもしょうがないのでは？ -- いえ、それなりの意味はあると思いますよ。

反射的有向グラフ

1-圏、つまり普通の圏は、標準的には*2dom, cod, id, compで定義されます（http://d.hatena.ne.jp/keyword/%b7%f7%cf%c0）。このなかでcompが結合なので、これを忘れるとdom, cod, idになります。射（morphism）の集合*3をM、対象（object）の集合をOとすると、dom, cod:M→O、id:O→M という写像となります。

Mは矢印（有向線分）の集合、Oは点の集合と思っていいので、dom(f)は矢印fの始点、cod(f)は矢印fの終点です。よく知られた言葉を使うなら、(E, O, dom, cod)は有向グラフです。id:O→Eは、グラフの頂点aごとに特別な辺id(a)を対応させます。id(a)のような特別な辺を備えた有向グラフは反射的有向グラフといいます。

ちなみに、「反射的」の語源は、f:a→b という辺があるとき a≦b と書くことにすると、辺id(a)の存在から、関係≦の反射律 a≦a が成立するからです。結合が定義されていれば、推移律も保証されます（今回は結合を考えませんが）。

反射的有向グラフの高次元化

1-圏から結合を忘れれば反射的有向グラフです。となると、n-圏から結合（複数ある）を忘れたモノは、反射的有向グラフの高次元版でしょう。そのようなモノを構成していくことにします。

グラフは（有向であれ無向であれ）、0次元の点と1次元の線を素材にして出来上がっています。高次元のグラフはより高次元の素材を必要とします。その素材をセル（胞、胞体）と呼びます。セルとして、三角形や四面体を使った図形は単体的複体（simplicial complex）、四角形や直方体を使った図形は方体的複体（cubical complex）と呼ばれています。任意の多角形、多面体をセルとして許す場合もありあます*4。

n-圏の定義でも、セルとして単体（三角形、四面体の一般化）や方体（四角形、直方体の一般化）を採用する流儀もありますが、一番簡単なのは二辺形、二面体の一般化である球体（globe）を使う方法でしょう。球体とは言っても、まるいかどうかが問題ではなくて、辺、面、点などを2個持つことが本質です。球体については、「おとぎ話としてのn-圏 -- 計算できる図形達の世界」で説明しています。

球体を使うアイディアはバタニン（Michael Batanin）によるようです。「普通のまるい図形」との混同を避けたいときは「バタニンの球体」と呼ぶことにします。バタニンの球体をセルとする図形は球体的複体（globular complex）ですが、より短く球複体と呼ぶことにします*5。

n次元の球複体

球複体の定義をハッキリさせましょう。1次元の球複体は反射的有向グラフなので、反射的有向グラフの定義を参考にします。点、線（有向辺）以外に、面やらもっと高次元の球体も素材となります。が、dom、cod、idはほとんど同じように定義できます -- そこが球体のいいところです。複体（図形）Cを構成するk次元球体の集合をC(k)と書くことにします（「おとぎ話としてのn-圏 -- 計算できる図形達の世界」）。C(k)→C(k-1) の形のdom、codは、dom(k→k-1)、cod(k→k-1)と書きましょう。同様に、C(k)→C(k+1) の形のidは、id(k→k+1)です。

以下、上付きの丸括弧は省略します、上付きは累乗じゃないですよ。n = 3の場合を考えると、dom3→2, cod3→2:C3→C2, dom2→1, cod2→1:C2→C1, dom1→0, cod1→0:C1→C0, id0→1:C0→C1, id1→2:C1→C2, id2→3:C2→C3 の合計9個の写像を考えます。一般のnに対しては3n個です。特に n = 1 のときは、dom1→0, cod1→0, id0→1 の3個です。

上付きの (k→k-1) などは省略することもあります。また、domk→k-1よりdomk-1←kのほうが見やすいこともあるので、←記法も使います。幾何学では、dom, codが面写像（face map）、idを退化写像（degeneracy map）とも呼びます。

1次元、つまり反射的有向グラフのとき、次の等式が成立していました。

  1. (dom(id(a)) = a
  2. (cod(id(a)) = a

2次元のときを考えると、2-セルαに対して次の等式が成立することは、図から明らかでしょう。

  1. dom(dom(α)) = dom(cod(α))
  2. cod(dom(α)) = cod(cod(α))


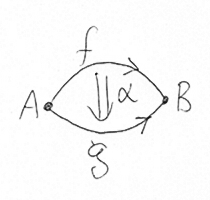
※絵の説明はコチラ

これらを一般化した形で、各次元のdom, cod, idに対して次の等式を要請します。

  1. domk-2←k-1(domk-1←k(x)) = domk-2←k-1(codk-1←k(x)) （x∈Ck, k≧2）
  2. codk-2←k-1(domk-1←k(x)) = codk-2←k-1(codk-1←k(x)) （x∈Ck, k≧2）
  3. domk←k+1(idk+1←k(x)) = x （x∈Ck, k≦n-1）
  4. codk←k+1(idk+1←k(x)) = x （x∈Ck, k≦n-1）

1個の3次元球体を、2つの面、2つの辺、2つの点から組み立てた図形と考えると、各次元のdom, cod, idは次の図のようになります。


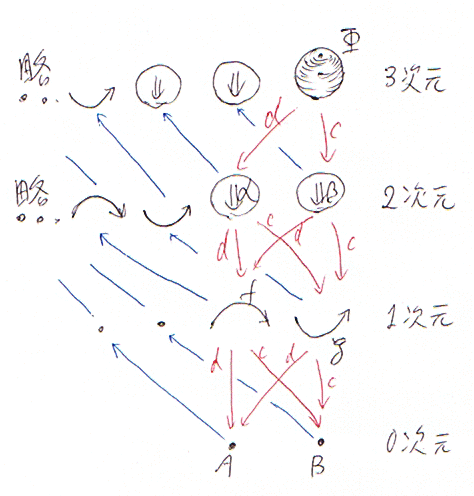
※絵の説明はコチラ

球複体から分かること

今日はここまでです。上で導入したdom, cod, idを少しだけ一般化したほうが扱いやすくなります。そして、ホムセットの一般化であるホム複体を考えます。ホム複体は、共端な２つのk-セルを両端（境界）とするようなセルの集合に再び球複体の構造を入れたものです。ホム複体をよく観察すると、負次元の存在が見えてくるはずです。

*1:バタニンの方法以外にいろいろな流儀がありますが、僕は他の方法は知りません。

*2:定義の方法はいろいろあります。

*3:集まりの大きさについてトヤカク言わないことにします。

*4:「セル」、「セル複体」を、任意形状の素材と、その素材を組み合わせた図形の意味で用いることも多いようです。

*5:球集合（globular set）、球対象（globular object）なんて言葉もありますが、幾何学的な匂いが消えてしまうので「複体」を残します。