インデックス付き圏(indexed category)の話をしても全くウケないのは承知でもう一回。
インデックス付き圏があると、それに対してグロタンディーク構成(Grothendieck construction)とか平坦化(flatten)とか呼ばれる操作をしてファイバー圏(fibred/fibered category)が作れます。とりあえず、ファイブレーションは考えないで、インデックス付き圏から1つの圏を作る手順を示します。
インデックス付き圏の雰囲気は、まー、次の絵のような感じです。
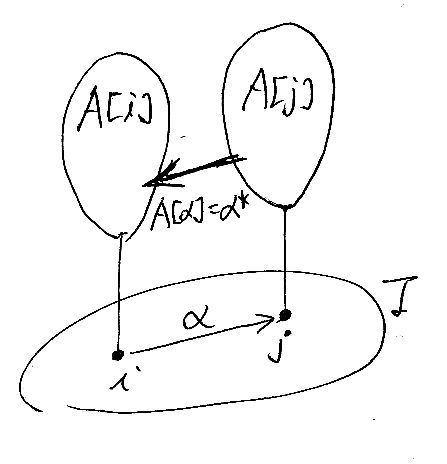
Iがベース圏(インデックスの圏)で、Iの対象 i, j などの上に木が生えているみたい。それぞれの木 A[i], A[j] がまた圏になっています。ベース圏(地面ですね)に射 α:i→j があると、木のあいだに逆向きの関手 α* が走っています。木の根っ子どうしがαで繋がっていれば、木の幹や葉っぱ達はα*で対応する、という構造。
さて、ベース圏の対象iと、i上の圏A[i]の対象aのペア(i, a)の全体を考えます。これは、圏A[i]達の対象を全部寄せ集めた集合を作ることになっています。上の絵で言えば、地面に生えているすべての木の葉っぱを全部寄せ集めたような集まりを考えるのです。こうしてできた (i, a)達の集合をXとします。
次に、(i, a)から(j, b)への射を、ペア(α、f)として定義します。ここで:
- αは、圏Iのなかの i→j という射
- fは、圏A[i]のなかの a→α*(b) という射
先に定義した集合Xを対象の集合として、いま定義した射達を一緒に考えると圏の素材になります。あと、結合(composition)と恒等(identity)が必要ですね。
結合の方法を絵に描くと、だいたいこんな(↓)感じかな。
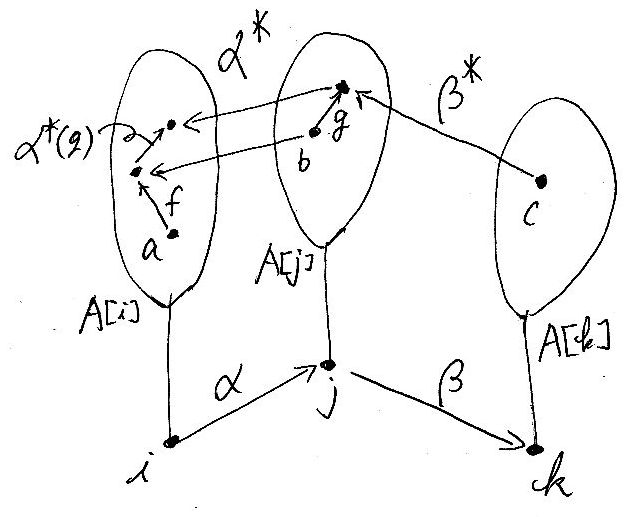
(α, f):(i, a)→(j, b) と (β, g):(j, b)→(k, c) を結合しましょう。念のために確認しておくと:
- α:i→j in I
- f:a→α*(b) in A[i]
- β:j→k in I
- g:b→β*(c) in A[j]
(α, f) と (β, g) の結合を (γ, h) とすると、(γ, h):(i, a)→(k, c) ですが、(γ, h) は次のように定義されます。
- γ = α;β :i→k in I
- h = f;α*(g) : a→α*(β*(c))
恒等射の定義は自明でしょう。結合律と単位律も、順番に調べていくだけです。
絵を見ると、ファイバーバンドルの接続(平行移動)とかと似た概念であることが分かります。ここらへんの話は、「圏の幾何学」という趣<おもむき>がありますね。