ストリンググラフとストリング図

「ストリング図とストリンググラフ、何が違う？」で触れたストリンググラフを、もう少し詳しく説明します。

内容：

アンチ反射的単純有向グラフ

グラフ理論に関する定義をズラズラと並べます。退屈ですが、言葉の確認です。

有向グラフは、頂点（vertex）の集合をV、辺（edge）の集合をEとして、四つ組 (V, E, src, trg) で定義します。ここで、

• src:E→V は、辺にその始頂点（source vertex）を対応させる写像、
• trg:E→V は、辺にその終頂点（target vertex）を対応させる写像。

勝手に取った2つの頂点 a, b に対して、src(e) = a, trg(e) = b となる辺eが高々一本しかないとき、その有向グラフは単純（simple）である、と言います。なお、単純グラフの定義として「自己ループ辺も認めない」を追加するときもあります。自己ループ辺とは、src(e) = trg(e) となる辺eです。

(V, E, src, trg) が単純有向グラフのとき、E⊆V×V とみなしてかまいません。第1射影 V×V→V をEに制限してsrcとして、第2射影 V×V→V をEに制限してtrgとします。今回は、単純有向グラフしか扱わないので、E⊆V×V と考えます。srcとtrgは射影として自動的に決まるので、単純有向グラフを単に (V, E) と書くことにします。

有向グラフが反射的（reflexive）とは、self:V→E という写像があり、src(self(a)) = a, trg(self(a)) = a となることです。selfは、頂点に対して自己ループ辺を対応させる写像です。単純有向グラフのときは、反射的であることは次のように表現できます。

• Δ_V⊆E

Δ_Vは、{(a, b)∈V×V | a = b} という対角集合です。このとき、self(a) := (a, a) としてselfを定義できます。このselfは一意的に決まってしまいます。

単純有向グラフがアンチ反射的（anti-reflexive）であるとは次のことだとします。

• Δ_V∩E = 空集合

これは、「反射的でない（反射的の否定）」ではなくて、自己ループ辺を全く持たないことです。

今後考えるグラフはアンチ反射的単純有向グラフ（狭義の単純有向グラフ）だけです。つまり、自己ループ辺はありません。しかし、アンチ反射的単純有向グラフの準同型写像を定義するときに自己ループ辺を使います。

(V, E) と (V', E') がアンチ反射的単純有向グラフだとして、f = (f^vert, f^edge) は写像の組で、

• f^vert:V→V'
• f^edge:E→(E'∪Δ_V')

とします。f^edgeの余域に自己ループ辺を含めていることに注意してください。

f = (f^vert, f^edge) がアンチ反射的単純有向グラフの準同型写像（homomorphism）であるとは、次を満たすことです。

• src(f^edge(e)) = f^vert(src(e))
• trg(f^edge(e)) = f^vert(trg(e))

(V, E) の辺eを潰すときに、Δ_V'の自己ループ辺を使うのです。辺を潰す手段がないと、例えば自明な離散グラフ ({a}, {}) への準同型写像を作ることが出来ません -- それでは不便なので、ちょっと技巧的な定義としたのです。

ストリンググラフとラベリング

ストリンググラフは、アンチ反射的単純有向グラフに対してさらに構造と条件を加えたものです。事前に「ストリング図とストリンググラフ、何が違う？」を読んでおくと理解が早いと思います。

アンチ反射的単純有向グラフ (V, E) の頂点の集合Vが、V = W + N と直和分解されているとします。Wに所属する頂点をワイヤー頂点（wire vertex）、Nに所属する頂点をノード頂点（node vertex）と呼びます。通常、「頂点」と「ノード」は同義語ですが、ここでは区別します。

頂点集合がワイヤー頂点とノード頂点に分割されたアンチ反射的単純有向グラフを (W, N, E) と書くことにします。(W, N, E) がストリンググラフ（string graph）だとは、次を満たすことです。

• ワイヤー頂点の入次数（in-degree）と出次数（out-degree）の組 (indeg, outdeg) は、次のいずれかに限る：(0, 1), (1, 1), (1, 0)
• 任意の辺eに対して、src(e)かtrg(e)の少なくとも1つはワイヤー頂点である。

頂点の入次数とは、その頂点に入る辺の本数、出次数は出る辺の本数です。

ストリンググラフの定義から、ワイヤー頂点はその入次数／出次数により三種類に分類できます。

1. 入次数が0であるワイヤー頂点を進入境界頂点（incoming boundary vertex）と呼ぶ。
2. 出次数が0であるワイヤー頂点を退出境界頂点（outgoing boundary vertex）と呼ぶ。
3. 入次数、出次数ともに1であるワイヤー頂点を内部ワイヤー頂点（interior wire vertex）と呼ぶ。

進入境界頂点と退出境界頂点をあわせて境界頂点（boundary vertex）と呼びます。

次の図（http://arxiv.org/pdf/1504.02716.pdf）の(b)はストリンググラフで、2個の進入境界頂点、1個の退出境界頂点、6個の内部ワイヤー頂点を持ちます。

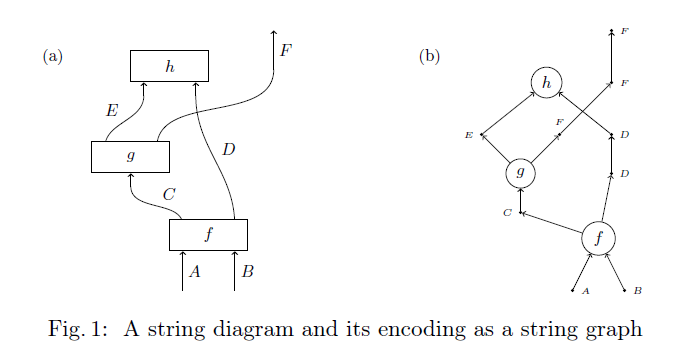
ストリンググラフの準同型写像（homomorphism）は、下部構造（underlying structure）であるアンチ反射的単純有向グラフの準同型写像で、ワイヤー頂点をワイヤー頂点に、ノード頂点をノード頂点に写すものとして定義します。

(W, N, E) がストリンググラフのとき、ラベルの集合をLとして、写像 label:(W + N)→L が次の条件を満たすときラベリング（labeling）と呼びます。

• v, wが隣接するワイヤー頂点のとき、label(v) = label(w)

「v, wが隣接する」とは、「src(e) = v かつ trg(e) = w」または「src(e) = w かつ trg(e) = v」となる辺eがあることです。

ストリンググラフでは、ワイヤー頂点が辺を代表していると考えられるので、辺に対するラベルは考えません。

ストリンググラフ（ストリング図のグラフ化）を圏論で使うときは、ラベル集合に圏Cを使い、

• ワイヤー頂点には、圏Cの対象をラベルとする
• ノード頂点には、圏Cの射をラベルとする
• 隣接する頂点に圏論的な条件を付ける

とします。

ストリンググラフの描画＝ストリング図

ストリンググラフは、ストリング図に対応するデータ構造として生み出されました（「ストリング図とストリンググラフ、何が違う？」参照）。幾何的対象としてストリング図があり、その組み合わせ構造を抽出したものとしてストリンググラフがあるわけです。

しかしここでは、先にストリンググラフありき、として、ストリンググラフの幾何的描画（geometric rendering）／幾何的実現（geometric realization）としてストリング図を導入します。

(W, N, E) をストリンググラフとします。Xをなんらかの位相空間だとして、連続写像 ψ^vert:(W + N)→X と ψ^edge:E×[0, 1]→X の組 ψ = (ψ^vert, ψ^edge) を考えます。ここで、W + N とEには離散位相を入れて、[0, 1]は実数の単位区間で、普通の位相です。ψ = (ψ^vert, ψ^edge) が次の条件を満たすとき、ψをストリンググラフ (W, N, E) の描画（rendering）と呼びます。

e∈E に対して、ψ^edge の {e}×[0, 1] への制限を ψ_e:{e}×[0, 1]→X として：

1. ψ_e(0) = ψ^vert(src(e))
2. ψ_e(1) = ψ^vert(trg(e))

写像ψにより、グラフの辺がX上の“線分”として実現されて、その両端が、グラフ構造における両端（始頂点と終頂点）に一致している、ということです。

単位区間 [0, 1] の内部である開区間を (0, 1) と書くことにして（これは紛らわしい記法ですが、文脈で判断してください）、ψの E×(0, 1) への制限が単射のとき、埋め込み描画（embedding rendering）と呼ぶことにします。いつでも埋め込み描画が可能なわけではありませんが、埋め込み描画は扱いやすい描画です。

ストリンググラフ (W, N, E)、キャンバスとなる空間X、描画写像 ψ = (ψ^vert, ψ^edge) によりストリング図（string diagram）が定義されます。

キャンバス空間Xに変な空間を考えるとややこしくなって嬉しくないので、通常は、素直な空間である多様体を使います。

描画の例

ストリンググラフの描画先であるキャンバス空間として一番簡単なものは、ユークリッド平面R²でしょう。[0, 1]→R² という写像なら微分可能性を考えることができるので、辺eに対するψ_eは（適当な回数の）微分可能性を要求しましょう。また、微分係数（速度ベクトル）はいたるところゼロでないと仮定します。

上記のような仮定をすれば、描画 ψ = (ψ^vert, ψ^edge) は、かなり扱いやすいものになります。ストリンググラフがラベル付きである場合は、ラベル値を色や文字列で表現すれば、現実的な描画が可能です。

辺eを描く写像 ψ_e:{e}×[0, 1]→R² に色々な関数を選べますが、一番簡単なのは1次関数（アフィン線形写像）です。辺の描画に1次関数を使った描画を区分線形描画（piecewise linear rendering）と呼びます。

ワイヤーの曲線は、内部ワイヤー頂点をたくさん取れば折れ線（つまり区分線形描画）で近似できます。よって、区分線形描画だけを考えても、考察対象が限定されてしまうことはありません。

その他の話題

描画のキャンバス空間として、円板や矩形を考えたほうがいいことがあります。そのときは、円板や矩形の境界と、ストリンググラフの境界頂点との関係も考慮します。さらに、円環（annulus）のように穴の開いた図形をキャンバスにすることもあります。

キャンバスに描かれた“絵”としてのストリング図に対して、それらの組み合わせ（composition, combination）を考えると、ストリング図の全体が圏、複圏（オペラッド）、多圏などの構造を持つことになります。