一般化されたマイヒル／ネロードの定理 1：準備と事例 - 檜山正幸のキマイラ飼育記 (はてなBlog)

一般化されたマイヒル／ネロードの定理について「いつかキチンと書こう」と思いながら10年が経過してしまいました。「もっと一般化したい」「前提を減らしたい」「キレイにまとめたい」「高次元化したい」とかの希望はあるのですが、それを言っているとさらに先延ばしになってしまうので、とりあえず現時点でハッキリと言えることを、なるべく正確に記述することにします。

一回に書き切れる量ではないので、何度かに分けます。でも、次回が数年先にならないように努めます。

内容：

今までの経緯＝先延ばしの歴史
用語法の注意
プレオートマトンの定義
伝統的オートマトン
反変オートマトンとオートマトンの双対
整数スタックの例
指標グラフの操作：制限と除去
開始頂点族、識別頂点族、固定化関手
オートマトンの定義：開始と識別の構造
今回のまとめ

シリーズ記事リンク：

今までの経緯＝先延ばしの歴史

マイヒル／ネロードの定理のソフトウェア的解釈を、僕が最初にメモっているのは、2006年5月のようです。

ネロード同値とか（だいぶ未整理、用語法・記法も曖昧）

6年後の2012年4月の記事「メイヤー代数、メイヤー指標、メイヤーオートマトン」において：

到達可能性と識別可能性という概念を使い、マイヒル／ネロード（Myhill/Nerode）風の定理を導きます -- この話は長くなるのでまた別な機会にしましょう。

記事タイトルに含まれる「メイヤーオートマトン」（Mayer automaton）は、通常の定義に比べて一般化されたオートマトンのことです。上記引用記事の10日ほど後の記事「メイヤーオートマトンに関するマイヒル／ネロードの定理を宣伝する」で、メイヤーオートマトン（＝一般化されたオートマトン）に対するマイヒル／ネロードの定理が示せたら何が嬉しいのか、どんなご利益があるのかを説明しています。

その後、関連する概念や予備知識の説明を少しだけしたことはあります（下の記事など）。

しかし、完全な記述はないので、これからチャント書こうと思います。過去の記事への参照はしますが、説明を丸投げはしないで、なるべく自己完結的になるようにします。ただし、一般性が高い予備知識まで再度説明することはしません。~~また、動機や背景の説明は省略することが多くなると思います。~~←けっこう詳しく書くつもり。

用語法の注意

これから扱う“オートマトン”は、一般化されたオートマトンです。これは、数年前に僕がメイヤーオートマトンと呼んでいたものと同じです。単に「オートマトン」と言ったら、一般化されたオートマトンを意味することにします。つまり、

一般化されたオートマトン＝メイヤーオートマトン＝オートマトン

形式言語理論／オートマトン理論の教科書にあるような通常のオートマトンは、伝統的オートマトン（traditional automaton）と呼ぶことにします。伝統的オートマトンについても、一般化されたオートマトンについても、後でチャント定義します。

伝統的オートマトンに対するマイヒル／ネロードの定理（Myhill–Nerode theorem）は、正規言語とオートマトンの関連を述べた定理ですが、正規言語には特に拘らない定式化をします。一般化されたマイヒル／ネロードの定理は、一般化されたオートマトンに対するマイヒル／ネロードの定理のことです。単に「マイヒル／ネロードの定理」と言ったら、一般化されたマイヒル／ネロードの定理を意味することにします。つまり、

一般化されたマイヒル／ネロードの定理＝一般化されたオートマトンに対するマイヒル／ネロードの定理＝マイヒル／ネロードの定理

基本概念を準備して補題を積み重ねれば、一般化されたマイヒル／ネロードの定理に到達します。全体の構図は頭にありますが、細部まで詰めたことはないので、それをこれからやる予定です。

プレオートマトンの定義

ここでは、（一般化された）オートマトンとして関手オートマトンを採用します。関手オートマトンについては、次の過去記事で扱ってますが、必要な事項はすぐ下で述べます。

オートマトンの定義を書き換えてみる

オートマトンは始状態（初期状態）と終状態を持ちますが、それらは後で付加することにして、プレーンな状態遷移系に相当するプレオートマトンから考えましょう。プレオートマトン（preautomaton）とは、Cを小さい圏として、F:C→Set という形の関手Fのことです。ただし、圏Cはグラフ（有向グラフ）から自由生成されたものに限定します。Φをグラフとして、Cは C = FreeCat(Φ) と書けることを常に前提するわけです。グラフをギリシャ文字大文字で書く理由は後（「伝統的オートマトン」の節）で説明します。グラフから自由生成された圏（自由圏、パスの圏、道の圏）については、次の記事を参照してください。

グラフと圏のあいだには次の随伴関係があります。

CAT(FreeCat(Φ), Set) $\stackrel{\sim}{=}$ GRAPH(Φ, Forget(Set))

ここで、CATは“必ずしも小さくない圏”の圏、GRAPHは“必ずしも小さくないグラフ”の圏です。大きな圏Setが含まれるので「必ずしも小さくない」という断り書きが必要になります。FreeCat:GRAPH→CAT は自由生成する関手で、Forget:CAT→GRAPH は忘却関手です。

この随伴関係 FreeCat -| Forget があるので、自由圏FreeCat(Φ)からの関手とグラフΦからのグラフ準同型写像は1：1に対応します。この1：1対応により、関手とグラフ準同型写像を同じ記号で表すことがあります（記号の乱用です）。例えば、(F:FreeCat(Φ)→Set) ←→ (F:Φ→Set) のように、同じFで関手とグラフ準同型写像を表します。

プレオートマトンとは自由圏からの関手だったので、F:FreeCat(Φ)→Set または F:Φ→Set としてプレオートマトンを表すことになります。関手Fが値を取る圏をSet以外にすると、別種のプレオートマトンを定義できます。例えば、F:Φ→Rel なら、Fは非決定性プレオートマトンです。kを適当な体として、F:Φ→Vect_k なら、Fはk-線形プレオートマトンになります。しかしここでは、関手の値の圏はSetに限ります。つまり、決定性プレオートマトンだけを考えることになります。

後（「オートマトンの定義：開始と識別の構造」の節）で述べるように、プレオートマトンとオートマトンの差はたいしてないので、プレオートマトンをオートマトンと呼ぶこともあります。特に強調したいときだけ「プレ」を付けることにします。

伝統的オートマトン

伝統的オートマトンを、先に定義した関手(プレ)オートマトンとみなす方法を見ておきましょう。

伝統的オートマトンは、A = (Γ, Q, δ, q₀, T) として定義されます。ここで：

Γはアルファベット（alphabet）です。どんな集合でもかまいません。伝統的にアルファベットはΣで表されることが多いのですが、大文字シグマを別な意味で使う可能性があるので大文字ガンマ（Γ）を使いました。
Qは状態空間（state space）です。空でなければどんな集合でもかまいません。文字Sを使わなかったのは、Sを後で別な意味で使うからです。
δは遷移写像（transition map）で、δ:Q×Γ→Q。これも何の制限もありません。
q₀は始状態（initial state）。q₀∈Q なら何でもいいです。
Tは終状態（final state, terminal state）の集合で、T⊆Q。Tは空でない部分集合です。

A = (Γ, Q, δ, q₀, T) から、グラフΦと関手 F:Φ→Set を作ります。再度注意しますが、関手とグラフ準同型写像を適宜同一視しています。F: Φ→Set は、ホントは関手じゃないけど、C = FreeCat(Φ) の関手に一意的に拡張できるので、“関手”とも呼びます。

これから作るグラフΦは、伝統的オートマトンAの指標グラフ（signature graph）、または単に指標（signature）と呼びます。インスティチューション理論では、指標をギリシャ文字大文字で表す習慣があるので、それに従ってギリシャ文字大文字を使ったのです。

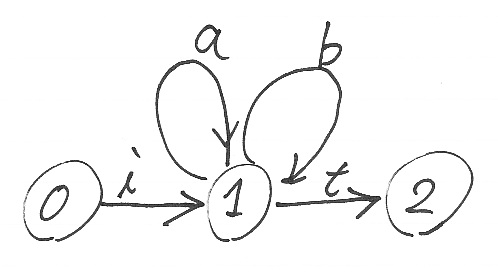
Φはグラフですが、圏と同様な記法を使って、頂点の集合を|Φ|、x, y∈|Φ| に対して2頂点のあいだの辺の集合をΦ(x, y)で表します。伝統的オートマトンAに対する指標グラフΦは次の通りです。

|Φ| = {0, 1, 2}
Φ(0, 1) = {i}
Φ(1, 1) = Γ
Φ(1, 2) = {t}
それ以外のΦ(n, m)は空集合。

指標グラフΦは、アルファベットΓだけから決まり、その他の構成要素は関与してないことに注意してください。以下は、Γ = {a, b} の場合の指標グラフです。

次に、F:Φ→Set を定義します。（定義にインフォーマルなラムダ記法を使ってます。ラムダ記法については、過去記事「JavaScriptで学ぶ・プログラマのためのラムダ計算」、「絵を描いて学ぶ・プログラマのためのラムダ計算」などを参照してください。）

F(0) = 1 （1は特定された単元集合、1 = {0}）
F(1) = Q
F(2) = B （Bは真偽値の集合で B = {true, false}）
F(i):1→Q は、0|→q₀ で決まる写像。
a∈Γ に対するF(a):Q→Q は、λs∈Q.δ(s, a) で決まる写像。
F(t):Q→Bは、s∈Tならtrue、そうでないならfalseで決まる写像。

以上で、伝統的オートマトン A = (Γ, Q, δ, q₀, T) から指標グラフΦと関手（グラフ準同型写像）F：Φ→Set が決まりました。FはAの情報をすべて持っているので、関手Fから伝統的オートマトンAを再現できます。

Γ = Φ(1, 1)
Q = F(1)
δ(s, a) = F(a)(s) （F(a):Q→Q）
q₀ = F(i)(0) （F(i):1→Q）
T = F(t)^-1(true) （F(t):Q→B）

反変オートマトンとオートマトンの双対

決定性オートマトンだけの範囲では、双対性の議論はあまりキレイにまとまりません。僕が何か見落としているのかも知れないですが、非決定性オートマトンまで含めないと本質的にうまくいかない、って可能性もあります。しかしそれでも、双対を考えることは重要なテクニックです。

先に注意したように、グラフ準同型写像 F:Φ→Set に対応する関手も同じFで表します。C = FreeCat(Φ) とすると、F:C→Set （関手）とも書きます。以下、CはFreeCat(Φ)の意味で使います。

オートマトンFはCからの共変関手でしたが、反変関手 G:C^op→Set を考えることもできます。関手として反変であるオートマトンを反変オートマトン（contravariant automaton）と呼びます。余オートマトン（coautomaton）、反対オートマトン（opposite automaton）でもいいと思います。加群との類似では左オートマトン（left automaton）と呼ぶべきでしょうが、左右の区別は書き方で変わってしまうので、「左」「右」を積極的に使う気はありません。

オートマトン F:C→Set があるとき、「Fの双対」が標準的に作れるかというと、それは出来ません。集合圏Setには標準的双対の概念がないからです。でも、人為的・恣意的な双対なら作れます。適当に V∈|Set| を選んで、Vに関して双対な反変オートマトンを構成します。

まず、集合圏SetにV-双対性を導入します。

集合Xに対して、X^*V := V^X。ここで、V^Xは、XからVへの写像の全体からなる集合（関数集合、指数）。
写像 φ:X→Y に対して φ^*V:Y^*V→X^*V を、φ^*V(ρ:Y→V) := φ;ρ と定義する。これは、φを前結合（pre-compose）しての引き戻しです。

X|→X^*V と φ|→φ^*V を一緒にすると、(-)^*V:Set^op→Set という反変関手が定義できます。V = B = {true, false} のとき、(-)^*Vは反変ベキ集合関手と同じものです。この V = B のケースが最もよく使う双対性です。

オートマトン F:C→Set のV-双対オートマトン（V-dual automaton）F^*Vを次のように定義します。

x∈|C| に対して、F^*V(x) := F(x)^*V
f∈C(x, y) に対して、F^*V(f) := F(f)^*V

FのV-双対オートマトンは反変オートマトンであることに注意してください。Gが反変オートマトンである場合は、GのV-双対オートマトンを作ると共変オートマトンになります。V-双対により反変と共変が入れ替わります。

正確には「共変オートマトンFのV-双対な反変オートマトン」とか言うべきですが、反変・共変は文脈で判断してください。また、Vを固定している状況では、F^*Vを単にF^*と書くことがあります。

A = (Γ, Q, δ, q₀, T) を伝統的オートマトンとして、F:Φ→Set を対応する関手オートマトンとします。V = B と固定して、Fの双対オートマトン F^* = F^*B を考えてみましょう。以下、Pow(X)はXのベキ集合です。

F^*(0) = B¹ $\stackrel{\sim}{=}$ B
F^*(1) = B^Q $\stackrel{\sim}{=}$ Pow(Q)
F^*(2) = B^B $\stackrel{\sim}{=}$ Pow(B)

同型である集合は互いに置き換えても実質は同じなので、次のように定義してしまいましょう。

F^*(0) = B = {true, false}
F^*(1) = Pow(Q)
F^*(2) = Pow(B) = {{}, {true}, {false}, {true, false}}

i:0→1, t:1→2 と a:1→1（a∈Γ）に対するF^*の値は次のようになります。

F^*(i):Pow(Q)→B は、λX∈Pow(Q).(if (q₀∈X) then true else false)。
F^*(a):Pow(Q)→Pow(Q) は、λX∈Pow(Q).{y∈Q | F(a)(y) ∈X}。
F^*(t):Pow(B)→Pow(Q) は、{true}|→T, {false}|→(Tの補集合) で定義される写像。

これで、Fの双対である反変オートマトンF^*が定義できました。この例から分かるように、FとF^*は強い対称性を持っているわけではありません。始状態と終状態が入れ替わっているようにも思えますが、実際には対称性は歪んでいます。対称性を得るには、個別の工夫が必要ですから、安易に対称性を期待してはダメです。

整数スタックの例

伝統的オートマトン以外のオートマトンの例も出しておきましょう。整数値を積むスタックを考えます。

スタックのインターフェイスを記述しましょう。インターフェイス記述言語は擬似言語ですが、なんらかのプログラミング言語を知っていれば意味はすぐ分かるでしょう。メイヤー先生については、「メイヤー先生の偉大さとCommand-Query分離」を参照してください。



interface IntStack {

 query: // メイヤー先生のクエリ

    isEmpty : this -> boolean;

    top : this -> int throws Error;

 command: // メイヤー先生のコマンド

    pop : this -> this;

    push : this, int -> this;

 creator: // 生成子（コンストラクタ）

    emptyStack : void -> this;

    singletonStack : int -> this; // 単一の要素を持つスタック

}

自分自身を表す暗黙のソート（型キーワード）thisを省略せずに書いています。popは例外を投げずに、空スタックに対しては何もしないだけとします。

[追記]thisはマズかったなー。thisの用法は、自分自身を表す型じゃなくて、変数のように使いますね。型は大文字始まりThisにして、this∈This とか、そんな感じにすればよかった。あるいは、interfaceの見出しに使ったIntStackを型の名前に使うか。

実際のthisの用法とは食い違いますが、絵（下）もあるので、モノグサしてそのままです。[/追記]

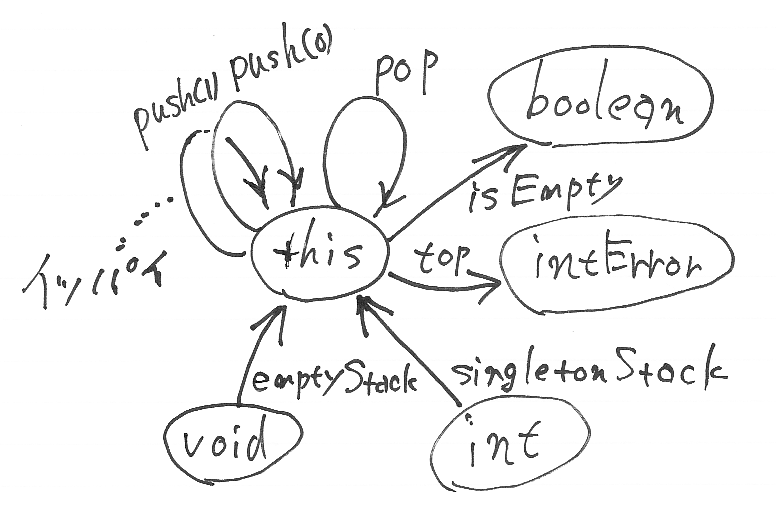
このインターフェイスIntStackに対応する指標グラフをΨを具体的に作りましょう。まず、|Ψ| = {this, void, boolean, int, intError} とします。intErrorは、例外が起きるかも知れない整数値の型です。グラフの辺に関して、pushだけは細工をします。pushは整数引数をもつので、引数の値ごとに1本の辺を作ります。push(0), push(1), push(-1), ... などがそれぞれ1本の辺になります。辺の集合は次のとおり：

Ψ(this, boolean) = {isEmpty}
Ψ(this, intError) = {top}
Ψ(this, this) = {pop}∪{push(n) | n∈Z}
Ψ(void, this) = {emptyStack}
Ψ(int, this) = {singletonStack}
その他のΨ(x, y)は空集合。

指標グラフΨの形状は次のようになります。Ψ(this, this)は無限本の辺を持つので描き切れません。

次に関手 G:Ψ→Set を定義します。以下、List(Z)は整数のリストの集合です。

G(this) = List(Z);
G(void) = 1 = {0}
G(boolean) = B = {true, false}
G(int) = Z
G(intError) = Z∪{error}

G(isEmpty), G(top), G(pop), G(push(n)), G(emptyStack), G(singletonStack) は、まーそれらしく定義します。すると、G:Ψ→Set は関手（グラフ準同型写像）となります。

指標グラフの操作：制限と除去

(プレ)オートマトンの指標としては、任意のグラフ（有向グラフ）を使えます。制限は何もありません。あえて指標グラフと呼ぶ理由は：

そのグラフΦから自由圏FreeCat(Φ)を作ることを前提している。
出来た自由圏FreeCat(Φ)から集合圏Setへの関手を考える心積もりがある。

指標グラフに対する2つの操作をここで定義しておきましょう。

はグラフΦの頂点の集合を表すのでした。X⊆

、つまりXを頂点全体の部分集合とします。新しいグラフΨを次のように定義します。

|Ψ| = X
Ψ(x, y) = Φ(x, y) （x, y∈X）

こうして作られるΨは明らかにΦの部分グラフになります。グラフ理論では、頂点の部分集合Xによる誘導部分グラフ（indueced subgraph）と呼ぶことが多いですが、ここでは圏論ぽい言葉使いをして、充満部分グラフ（full subgraph）と呼びましょう。充満部分グラフは、頂点の集合をXに制限したグラフとも言えます。ΦをXに制限したグラフ（充満部分グラフ）をΦ@Xと書くことにします。

同じく X⊆|Φ| として、|Φ|からXを取り除いて新しいグラフを作ることもできます。これは、「＼」を差集合として、|Φ|＼X にΦを制限することと同じです。念のために詳しく書くと：

|Ψ| = |Φ|＼X
Ψ(x, y) = Φ(x, y) （x, y∈(|Φ|＼X)）

このΨを、ΦからXを除去したグラフと呼んで、Φ＼X と書くことにします。定義より：

Φ＼X = Φ@(|Φ|＼X)

開始頂点族、識別頂点族、固定化関手

伝統的オートマトンには、始状態と終状態がありますが、一般化された(プレ)オートマトンには始状態／終状態の概念がまだありません。これから、始状態／終状態に類似の概念を導入します。そのためには、指標グラフに構造を与える必要があります。

Φを任意の指標グラフとします。頂点集合|Φ|の2つの部分集合S, Dを考えます。S⊆|Φ|、D⊆|Φ|、SもDも空でもかまいません。SとDの相互の関係（例えば「交わらない」など）は特に仮定しません。

上記の状況で、Sに属する頂点を開始頂点（starting vertex）、Dに属する頂点を識別頂点（distinguishing vertex）と呼びます。そして、集合Sは開始頂点族（family of starting vertexes）、集合Dは識別頂点族（family of distinguishing vertexes）と呼びましょう。

伝統的オートマトンの場合は、S = {0}, D = {2} です。開始頂点も識別頂点も1個ずつしかありません。それが伝統的オートマトンの特徴です。整数値を積むスタックでは、S = {void, int}, D = {boolean, intError} です。

グラフΦを、頂点の集合S∪Dに制限した部分グラフΦ@(S∪D)をΦ_visとも書きます。visはvisible（可視）の意味です（由来は後述）。Φ_visの定義を念のため書くと：

|Φ_vis| = S∪D
x, y∈S∪D に対して、Φ_vis(x, y) = Φ(x, y)

Φ_vis

に属する頂点を可視頂点（visible vertex）と呼びます。定義から、可視頂点は開始頂点または識別頂点のことです。Φの部分グラフΦ_visは可視部分グラフ（visible subgraph）と呼びます。

可視頂点でない頂点は隠蔽頂点（hidden vertex）と呼びます。グラフΦから頂点の集合S∪Dを除去した部分グラフΦ＼(S∪D)をΦ_hidとも書きます。hidはhidden（隠蔽）の意味です。Φの部分グラフΦ_hidは隠蔽部分グラフ（hidden subgraph）と呼びます。

可視／隠蔽という呼び方は、ゴグエン（Joseph Goguen）などの隠蔽代数（hidden algebra）理論に由来します。隠蔽代数も指標により定義されますが、指標に登場する頂点を可視と隠蔽に分類するのです。ただし隠蔽代数では（他の多くの文脈でも）指標に関する用語法はグラフ理論とは異なる言葉を使います。

グラフの用語	指標に固有な用語
頂点	ソート記号（または単にソート）
辺	オペレーション記号（または単にオペレーション）
可視頂点	可視ソート記号（または単に可視ソート）
隠蔽頂点	隠蔽ソート記号（または単に隠蔽ソート）
パス	項

可視ソート記号は、“既知の集合（型）”を表す記号、隠蔽ソート記号は“不可知な集合（型）”を表す記号です。両端が可視頂点（可視ソート）である可視辺（可視オペレーション）は、“既知の写像”を表すことになります。

したがって、可視頂点／可視辺（可視ソート／可視オペレーション）には前もって実際の集合／写像を割当てておきます。その割当てを K:Φ_vis→Set とします。Kはグラフ準同型写像ですが、関手ともみなします（関手なら FreeCat(Φ_vis)→Set）。Kは可視部分グラフの意味を固定するために使うので、固定化関手（fixtur functor）と呼びましょう。

可視／隠蔽の区別は、関手データベースでも使っています。次の図で、水色が可視頂点、ピンクが隠蔽頂点です。詳しくは「一般関手モデル：相対スキーマと相対インスタンス」を参照してください。

伝統的オートマトンの場合は、可視部分グラフは2個の頂点{0, 2}からなる離散グラフ（辺はない）で、K(0) = 1, K(2) = B で定義される K:{0, 2}→|Set| を固定化関手と思ってもかまいません。

これから考える指標グラフΦには、開始頂点族Sと識別頂点族Dが組み込まれているとして、Φ = (Φ, S, D) のように記します（記号の乱用）。また、固定化関手Kも入れた (Φ, K) = (Φ, S, D, K) をΦ/Kと略記します。ΦとKを組みにしたΦ/Kを、部分固定指標グラフ（partially fixed signature graph）、または単に部分固定指標（partially fixed signature）と呼びます。なお、「一般関手モデル：相対スキーマと相対インスタンス」では、部分固定指標グラフと同等な概念を相対スキーマと呼んでいます。

オートマトンの定義：開始と識別の構造

開始頂点族Sと識別頂点族Dが指定された指標グラフを Φ = (Φ, S, D) のように書きます。開始頂点族／識別頂点族を持つ指標Φと固定化関手 K:Φ_vis→Set を組にした部分固定指標Φ/Kがあるとき、Φ/K-オートマトン（Φ/K-automaton）とは、関手 F:Φ→Set であり、可視部分グラフΦ_vis上では固定化関手Kと一致するものです。言い方を換えると、(FをΦ_visに制限した関手) = K という等式が成立します。

F, G:Φ→Set が2つのΦ/K-オートマトンのとき、FからGへのオートマトン射（オートマトンの準同型写像）とは、関手Fから関手Gへの自然変換のことだとします。ただし、可視頂点上では自然変換の成分が恒等射となっているとします。αがオートマトン射であることは、α:F→G と書きますが、αを自然変換とみなすときは、α::F⇒G:C→Set のようにも書きます。

Φ/K-オートマトンとそのあいだのオートマトン射の全体からなる圏をAutom[Φ/K]と書くことにします。なお、Autom[-]という記法は「形式言語理論のための代数」でも使っていますが、今回の定義とは異なります。

最初に定義したプレオートマトンは、指標グラフが何の構造も持たず（SやDが指定されてない）、固定化関手Kも指定されてない状況で定義されました。Ψを無構造の（SやDが指定されてない）指標グラフとして、プレオートマトンの圏をPreAutom[Ψ]とすれば、忘却関手 Forget:Aotom[Φ/K]→PreAutom[Ψ] を定義できます。ここで、ΨはΦのS, Dを忘れたプレーンな指標グラフです（Kも忘却します）。

実は、プレオートマトンをオートマトンとみなす方法があります。Φ = (Φ, S, D) で、SもDも空集合のときは、可視部分グラフΦ_visは空グラフです。固定化関手は空グラフ（空圏）からの関手なので一意に決まります（が、無意味です）。つまり、S = D = 0 （0は空集合）の場合は、SもDも指定しないのと同じです。よって、プレオートマトンはオートマトンの特殊ケースとみなせます。

SまたはDが空の場合は：

Φ = (Φ, 0, 0) -- Φは無構造、Φ_visは空で、固定化関手Kは無意味。
Φ = (Φ, S, 0) -- Φは開始頂点族だけを持つ、固定化関手Kは Φ_vis = Φ@S 上で定義される。
Φ = (Φ, 0, D) -- Φは識別頂点族だけを持つ、固定化関手Kは Φ_vis = Φ@D 上で定義される。

ここで注意を述べておきます；開始頂点族と識別頂点族はデータ入出力ではありません。データ入出力を考えたいならまた別な定式化が必要です。データ入出力に対して、開始／識別と同じテクニックを使えることがありますが、開始／識別の構造を入出力に寄せ過ぎるのは好ましくありません。

今回のまとめ

今回やったことは、圏Autom[Φ/K]を定義したことです。Φは開始頂点族と識別頂点族を持つ指標 Φ = (Φ, S, D) であり、Kは固定化関手 K:Φ_vis→Set です。圏Autom[Φ/K]の対象が我々が扱うべきオートマトンですが、その実体は集合値関手です。したがって、圏Autom[Φ/K]は関手圏です。実際、オートマトンのあいだの射（準同型写像）は自然変換です。

今回、圏Autom[Φ/K]を定義した方法は、一般関手モデルとほとんど同じです。興味があれば、次の記事が参考になるでしょう。

（一般化された）マイヒル／ネロードの定理は、圏Autom[Φ/K]の構造を詳しく調べることで得られます。