そろそろ、メモ編にコソコソ書くことにしたほうが良さそうだけど… 「モノイド圏、豊饒圏、閉圏と内部ホム」と「閉圏、弱いラムダ計算、弱い論理」に少しは関係するから、いちおう本編に。
(C, ×, I, σ)を対称モノイド圏とします(σは対称性=入れ替え)。記号は「×」だけど、必ずしもデカルト積じゃなくてもかまわない。積×に対する指数は[-, -]で表すことにして、Cは閉(closed)で、指数[- , -]が定義可能だと仮定しましょう。
この状況で、(C, ×, I, σ, [-, -])の上でラムダ計算がある程度はできるんだけど、そのことを書くのではなくて(ダハハハハハ)、その“弱いラムダ計算”を成立させる根拠となる法則を書き下してみます。記号の使い方の説明で疲れて、“根拠の根拠”については全然書き切れなかった…(ここから下は、「だ・である」調。)
略記によって記法を簡素化
f:X×A→B、 g:Y→A だとして、fのAに関するカリー化(あるいはAに関する関数抽象)を f^ : X→[A, B] とする。そして、ev:[A, B]×A→B は評価(適用して計算、値を求める)射。このとき、
- f^×g:X×Y→[A, B]×A
- ev:[A, B]×A→B
- idX×g:X×Y→X×A
- f:X×A→B
のあいだに、
- (f^×g);ev = (idX×g);f
の関係がある。可換図式風(?)の表現(↓)、並んだイコールの上下が等しい。
X×Y -- f^×g → [A, B]×A -- ev → B ======================================= X×Y -- id_X×g → X×B -- f → B
これが、対称モノイド閉圏上の“弱いラムダ計算”のキモなのね。より具体的に言えば、これがβ変換(という構文的操作)の意味論(semantics, denotation)を与える。
idXをxのように対応する小文字で書いて、結合は「・」を使って反図式順、積 u×v を (u, v) のように書けば、
- ev・(f^, g) = f・(x, g)
f^はAに関する抽象だったからλa.fと書いて、「・」は適宜省略、適用評価に相当する ev・(u, v) をuとvの二項演算と考えて、中置演算記号としての空白を使って u v と書けば、
- (λa.f g) = f(x, g)
左辺の括弧は“まとまり”をつけるため、右辺の括弧は一種のタプリング(実体はモノイド積)を表す演算記号(-, -)の一部。ここまで略記すると、インフォーマルな記号使用に近くなる。まー、空白を演算記号に使うのは余りにヒドイから、別な記号で適用評価を明示するか、結合の「・」のほうを省略しない約束のほうが良さそうだけど。
例えば、適用評価を▽とかにして、-(ハイフン)を型Xの無名変数(関数抽象から逃れた残余の変数)だとすれば、
- f^▽g = f(-, g)
だいたいのところこれは、f^ = λa.f とgの適用は、fに出現するaをgで置き換えたもの(その他の残った変数はそのまま)って意味だ。どんな記法が見やすいかは、もう趣味的な問題かな。
何でもちゃんと書いて記法を厳密化
射のカリー化(関数抽象)は、C(X×A, B)≒C(X, [A, B]) という随伴に起因する。C(X×A, B)→C(X, [A, B])という方向の集合間の写像をΛ(大文字ラムダ)で表すと、f^=Λ(f)。しかし、Λは、X, A, Bに依存するので、それもハッキリと書けば ΛX,BA(f)。Aだけ上付きにしたのは、「Aに関する関数抽象」ということを強調するため。
評価射evも、AとBに依存するのでevA,B:[A, B]×A→Bとハッキリと書く。と、先に出した法則は、
- (ΛX,BA(f)×g);evA,B = (idX×g);f
ところで、evA,Bってのはid[A, B]の反カリー化だから、(Λ[A, B],BA)-1(id[A, B])。これを使えば、
- (ΛX,BA(f)×g);(Λ[A, B],BA)-1(id[A, B]) = (idX×g);f
ニョエーーー、なんかグチャグチャじゃねーか。
根拠の根拠
前節の等式は、gをidAと置けば少し簡単な形になる。
- (ΛX,BA(f)×idA);evA,B = f
- (ΛX,BA(f)×idA);(Λ[A, B],BA)-1(id[A, B]) = f
右辺の簡略化には、idX×idA = idX×A を使った。この等式を図示すれば、次のようになる。
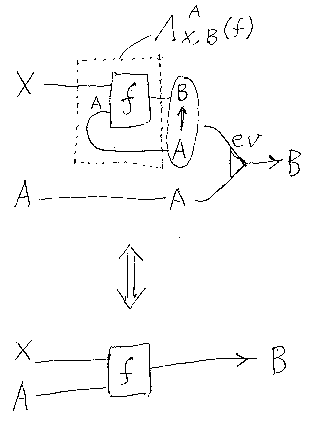
「この図、いったいなに?」と訝<いぶか>しく思うだろうが、実はコンパクト閉圏における“ものすごく弱いラムダ計算”に似せて描いた。“ものすごく弱いラムダ計算”とは結局、曲がった配線を許す回路図の描き方の技法に他ならない。
「なんで回路図なんじゃい?」ってか -- だって、ラムダ計算も自然演繹も回路図ですよ。「絵を描いて学ぶ・プログラマのためのラムダ計算 」で描いたようなラムダ項の構文解析木と、自然演繹の証明図が、回路図(フローグラフ)として同型である、ってのがカリー/ハワード対応。今、説明はしないけど*1。
さて、それにしても、先の等式はいったいどこから来るのか。まー、天下りに仮定してもいいのだけど、「どこから?」と問うなら、それは「(-×A)と[A, -]の随伴性」以外の理由は考えられない。「(-×A)と[A, -]の随伴性」を真面目に調べれば、カリー化(関数抽象)と適用評価の関係は出てくるはず。
実際のところ、Λ-1:C([A, B], [A, B])→C(A×B, B) という随伴を与える同型が自然変換(の成分)であることから、自然性を(適当なセッティングで)露骨に書き下すと、先の等式が得られる。このへんは、とにかくメイッパイあからさまに書き記す作業(身体的行為)をする以外にないですね。興味あるかたは、適切な練習問題ですからやってみてください。
[追記 date="翌日"]ヒントはコチラ。[/追記]
*1:実は、「閉圏、弱いラムダ計算、弱い論理」で書いた三位一体説を確認するためにカリー/ハワード対応を作ってみて、「なんだ、絵を描けばいいのか」と納得した次第。以前から知っていたわけじゃありません。