リー微分は共変微分か？ -- 代数的に考えれば - 檜山正幸のキマイラ飼育記 (はてなBlog)

[追記 date="2019-11-05"]この記事のなかで「リー微分も共変微分の一種だ」と書いてますが、それは間違いです。リー微分は共変微分ではありません。現時点では記事本文を修正してません（そのままです）が、なぜ間違いなのかの理由は次の記事に書いてあります。

間違った！リー微分は共変微分じゃない

[/追記][さらに追記 date="2019-11-06"]編集タグ（delとins）と追記で修正しました。delタグで削除された部分は取り消し線、insタグで挿入された部分は下線の表示になります。リー微分が共変微分ではないことの説明はこの追記です。間違っていた箇所はそのまま最後に置いてあります。
[/さらに追記]

「リー微分は共変微分か？」と聞かれたことがあります。定義からいって、リー微分は共変微分の一例ですではありません。~~単なる一例というだけでなく、標準的な共変微分と言っていいでしょう。~~

このことと関連する事項をできるだけ代数的に説明します。代数的な定式化の基本となることは、最近の記事でけっこう説明しています（今回の本文内でも適宜参照します）。

またここでは、ラムダ記法やカリー化を本質的に使うので、その解説もしています。今回登場する各種の微分演算はすべて、二項演算のカリー化により作り出されます。

内容：

はじめに
カリー化
ラムダ記法と無名ラムダ変数
微分適用と外微分
リー括弧とリー微分
間違い部分保続

はじめに

リー微分や共変微分は、多様体に関して定義されるものです。が、多様体も、その一部だけを見ればユークリッド空間の開集合と同じなので、局所的な議論なら、開集合 U⊆Rⁿ 上で行ってもかまいません。アトラスと層のメカニズムを使えば、局所的な議論を貼り合わせて全域的な結果を構成することが出来ます。

今回はアトラスも層も使いませんが、アトラスに関しては次の記事に書いています。

古典的微分幾何・ベクトル解析のモダン化：局所座標って何だ？

貼り合わせの道具である層に関しては：

ここではとりあえず、ユークリッド空間の開集合に関する議論を代数的に行います。それでも、多様体全域の議論と大きく変わるわけではありません。

代数的な定式化をすることにより、加群／ベクトル空間のテンソル積や、双線形写像のカリー化が、微分計算でも重要な役割を果たすことが分かると思います。

なお、「双対接続ペア」のときと同様に、次の想定で読んでもらえればいいです。

U ： Rⁿの開集合
R-可換環 A ：なめらかな関数のR-可換環 C^∞(U)
Der(A) ： U上の接ベクトル場のC^∞(U)-加群（有限生成自由加群）
Ω(A) ： U上の（1次の）微分形式のC^∞(U)-加群（有限生成自由加群）

カリー化

カリー化は、関数型プログラミング／型付きラムダ計算／デカルト閉圏などではお馴染みなんですが、通常の数学のなかだと意外と使われてなくて、それが理由で話が曖昧・晦渋になっていたりします。外微分もリー微分も、カリー化によって構成するんですけどね…… なので、ここでカリー化について説明しておきます。

今は圏の一般論をやりたくないので、集合と写像の例を使います。集合AからBへの写像の全体を Map(A, B) と書くことにします。Map(A, B) もまた集合になります。集合 Map(A, B) を B^A とか [A, B] とも書きます。以下では、[A, B] を使います。

f∈Map(A×B, C) に対して、g∈Map(A, [B, C]) と h∈Map(B, [A, C]) が次のように決まります。

(g(a))(b) := f(a, b)
(h(b))(a) := f(a, b)

gもhも、fから完全に決まる写像です。[B, C] = Map(B, C), [A, C] = Map(A, C) だったので、g:A→Map(B, C), h:B→Map(A, C) となります。

gもhもfから決まるので、次のように書きます。

g = f^∩
h = ^∩f

この記法の由来は、次の記事をザッと眺めれば分かるでしょう（由来を気にしないなら、見る必要はありません）。

関係する絵は次のようです（絵と記号の説明は「非対称閉圏のカリー化：記号法を工夫すれば、右と左の混乱も解消」参照）。

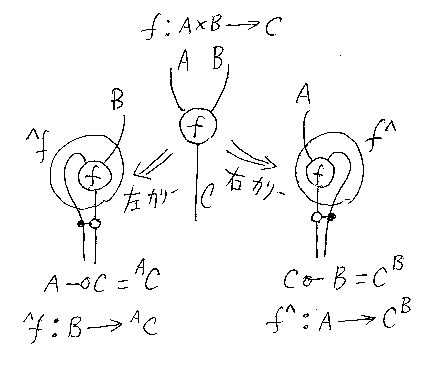
f^∩:A→[B, C] を f:A×B→C の右カリー化〈right currying〉、^∩f:B→[A, C] を f:A×B→C の左カリー化〈left currying〉と呼びます。

ラムダ記法と無名ラムダ変数

微分計算を行う際に、ラムダ記法／ラムダ計算も知っていたほうがいいよ、という話を次の記事でしました。

微分計算、ラムダ計算、型推論

上記記事で、次の過去記事を参照しています。ラムダ記法／ラムダ計算をまったく知らないなら、これらの記事が入門になるでしょう。

微分幾何でもラムダ記法は使ったほうがいい、という話は：

古典的微分幾何・ベクトル解析のモダン化：ラムダ記法の利用

ラムダ記法を使って、前節の右カリー化と左カリー化を定義すると次のようになります。

f^∩ := λx∈A.(λy∈B.f(x, y))
^∩f := λy∈B.(λx∈A.f(x, y))

通常のラムダ記法の代わりに、ラムダ変数（'λ'の直後に書く変数）をハイフンやアンダースコアにした式が使われます。例えば、λt∈R.(2×t + 1) の代わりに 2×(-) + 1 とかです。この略式の書き方では、ラムダ変数の型の情報は書けません。右カリー化と左カリー化を略式ラムダ記法を使って書くなら：

f^∩(a) := f(a, -)
^∩f(b) := f(-, b)

次のようにも使えます。

(-)^a := λx∈R.x^a
c^(-) := λx∈R.c^x

略式ラムダ記法で使われるハイフンやアンダースコアを無名ラムダ変数〈{anonymous | unnamed} {lambda}? variable〉といいます。

fの右カリー化 f^∩、左カリー化 ^∩f の、別な書き方を導入しておきます。

f_(-) := f^∩(-)
f^(-) := ^∩f(-)

つまり、

f_x := f^∩(x) = λy∈B.f(x, y)
f^y := ^∩f(y) = λx∈A.f(x, y)

あるいは、

f_x(y) := (f^∩(x))(y) = f(x, y)
f^y(x) := (^∩f(y))(x) = f(x, y)

この書き方は、方向微分、リー微分などで実際に使います。

微分適用と外微分

関数 f∈Map(A, B) と要素 a∈A に対して、関数の値 f(a) を求める操作を評価〈evaluation〉とか適用〈application〉と呼びます。評価／適用も関数なので、eval, appなどの名前で利用します。

app:Map(A, B)×A→B
app(f, a) = f(a)

R-可換環の導分に対して、適用写像を考えましょう -- その代数的準備としては、「双対接続ペア」の最初の節「可換環と加群」を読んでおいてください。ここから先で使う [-, -]_R, [-, -]_Aは、「カリー化」の節で使った“単なる写像の集合”ではなくて、“R-線形写像のR-ベクトル空間”、“A-線形写像のA-加群”です*1。

R-可換環Aの導分の集合 Der(A) は Map(A, A) の部分集合なので、適用を考えることができます。

app:Der(A)×A→A

Der(A) の要素（導分）は、「微分はライプニッツ法則に支配されている 3/3：領域導分と接ベクトル場」で述べた結果（領域導分定理）から、（解析的な）微分作用素と思っていいので、上記のappを微分適用〈{differential | derivative} application〉と呼び、Dと書くことにします。

D:Der(A)×A→A
D(X, a) = X(a)

Dはニ変数の関数（二項演算）ですが、第一変数を固定してR-線形（A-線形ではない）、第二変数を固定してA-線形になります。カリー化のときはこのことを考慮します。

前節のカリー化に関する記法を使うと：

D^∩:Der(A)→[A, A]_R
^∩D:A→[Der(A), A]_A

別な書き方は：

D_X := D^∩(X) = λa∈A.D(X, a)
D^a := ^∩D(a) = λX∈Der(A).D(X, a)

あるいは、

D_X(a) := (D^∩(X))(a) = D(X, a)
D^a(X) := (^∩D(a))(X) = D(X, a)

D^∩ = D_(-) は方向微分〈directional {derivative | differential}〉の記法として使います。^∩D = D^(-) は小文字'd'を使って、

d(-) = D^(-) = ^∩D(-)
d(a)(X) = D^a(X) = (^∩D(a))(X)

と表します。この d:A→[Der(A), A]_A が外微分〈exterior {derivative | differential}〉です。外微分とは、微分適用の左カリー化に過ぎないのです*2。外微分のdに、ミステリアスな印象を持つ必要はありません、少なくとも代数的には。

リー括弧とリー微分

[A, A]_R は、R-ベクトル空間とみたAからAへの線形写像の空間でした。足し算と実数スカラー倍は備わっています。さらに、写像の結合（合成）を掛け算（積）とみなすと、[A, A]_Rは、非可換（可換とは限らない）結合的単位的な多元環〈associative unital algebra〉となります。

任意の結合的多元環に対して、その交換子積〈commutator〉を考えると、リー環〈リー代数〉（Wikipedia項目「リー代数」）となります。この構成を [A, A]_R に適用して、リー環を作れます。その交換子積をリー括弧〈Lie bracket〉とも呼びます*3。

For X, Y ∈[A, A]_R,
[X, Y] := XY - YX = X $\circ$ Y - Y $\circ$ X

同じ大括弧〈角括弧 | ブラケット〉記号を使ってますが、指数（関数集合、線形関数加群）とは全然別で、二項演算です。混同しないように注意してください。

R-ベクトル空間として Der(A)⊆[A, A]_R ですが、実はリー環としても、Der(A)⊆[A, A]_R となります。つまり、次が成立します。

X, Y ∈Der(A) ならば、[X, Y]∈Der(A)

X, Y がライプニッツ法則を満たすとき、[X, Y] もライプニッツ法則を満たすことを確認すればいいので簡単です。

さて、リー括弧 [-, -] を L とも書くことにします。

[-, -] = L(-, -) = L : Der(A)×Der(A)→Der(A)

LはR-双線形な二変数関数（二項演算）なので、左カリー化／右カリー化を行うことができます。L(X, Y) = -L(Y, X) なので、左カリー化も右カリー化も（符号の差を除けば）同じことです。

Lの右カリー化 L^∩ = L_(-) : Der(A)→[Der(A), Der(A)]_R をリー微分〈Lie derivative〉と呼びます。リー微分の幾何的・解析的定義は、接ベクトル場が生成する流れ〈flow〉を使って行います（「流れとリー微分」参照）が、代数的には、リー微分はリー括弧（交換子積）の右カリー化です。

[追記]ここからずっと修正された文面。もとの間違っていた文面は最後に保存してあります。[/追記]

リー微分Lは、共変微分〈covariant derivative〉にはなりません。Lが共変微分であるためには、以下を満たす必要があります。

L_XはR-線形である。
1. L_X(Y + Z) = L_X(Y) + L_X(Z)
2. L_X(r・Y) = r・L_X(Y) for r∈R
L_(-)(Y)はA-線形（A-加群の準同型）である。
1. L_{(X + X')}(Y) = L_X(Y) + L_X'(Y)
2. L_(a・X)(Y) = a・L_X(Y) for a∈A
L_Xはライプニッツ法則を満たす。
L_X(a・Y) = X(a)・Y + a・L_X(Y) for a∈A

リー微分では、Yを固定しての X $\mapsto$ L_X(Y) に対するA-線形性が成立しません。その実例（反例）を出しましょう。

U = R² と置くと、自明に、UはR²の開集合です。A = C^∞(U) = C^∞(R²) と置きます。X, Y∈Der(A), a∈A を次のように決めます。

X = $\frac{\partial}{\partial x}$
Y = $\frac{\partial}{\partial y}$
a = λ(x, y)∈R².y

この X, Y, a に対して、L_a・X(Y) と a・L_X(Y) をそれぞれ計算します。

$\:\:\: L_{a\cdot X}(Y) \\ = [a\cdot X, Y] \\ = [y\frac{\partial}{\partial x}, \frac{\partial}{\partial y}] \\ = y\frac{\partial}{\partial x}\frac{\partial}{\partial y} - \frac{\partial}{\partial y} y\frac{\partial}{\partial x} \\ = y\frac{\partial}{\partial x}\frac{\partial}{\partial y} - (\frac{\partial y}{\partial y}\frac{\partial}{\partial x} + y\frac{\partial}{\partial x}\frac{\partial}{\partial y} ) \\ = -\frac{\partial}{\partial x} \\ \:\\ \:\:\:\: a\cdot L_X(Y) \\ = a\cdot [X, Y] \\ = y[\frac{\partial}{\partial x}, \frac{\partial}{\partial y}] \\ = y(\frac{\partial}{\partial x}\frac{\partial}{\partial y} - \frac{\partial}{\partial y} \frac{\partial}{\partial x}) \\ = y\cdot 0 \\ = 0$

一致しません。よって、リー微分Lが L_(a・X)(Y) = a・L_X(Y) for a∈A を満たすことは保証できないので、共変微分ではありません。

リー微分はライプニッツ法則は満たします。リー括弧のレベルでライプニッツ法則を書くと：

[X, a・Y] = X(a)・Y + a・[X, Y] for a∈A

これは定義に従った計算で示せます。念のため、計算を書いておきます。導分に対する関数によるスカラー乗法はドット、導分の結合と関数の積（可換環Aの積）は併置で表します。

b∈A に対して、

  [X, a・Y](b)
= (X(a・Y) - (a・Y)X)(b)
= (X(a・Y))(b) - ((a・Y)X)(b)

          (X(a・Y))(b)
        = X((a・Y)(b))
        = X(aY(b))
        = X(a)Y(b) + a(X(Y(b))
        = (X(a)・Y)(b) + (a・(XY))(b)

          ((a・Y)X)(b)
        = a(Y(X(b)))
        = (a・(YX))(b)

= (X(a)・Y)(b) + (a・(XY))(b) - (a・(YX))(b)
= ( X(a)・Y + a・(XY) - a・(YX) )(b)
= ( X(a)・Y + a・[X, Y] )(b)

[X, Y] = -[Y, X] であることから、リー微分 L_X(Y) = [X, Y] はXに関してもライプニッツ法則を満たしてしまいます。これが、Xに関するA-線形性が壊れてしまう理由です。

間違い部分保続

リー微分 L_(-) は、共変微分〈covariant derivative〉になります。「双対接続ペア // 接続付き加群」で、共変微分の定義の変種を幾つか挙げています。そのなかの4番目の定義がリー微分の定義としてふさわしいでしょう。（実数／関数によるスカラー乗法はドットで書いてます。）

L_XはR-線形である。

L_X(Y + Z) = L_X(Y) + L_X(Z)

L_X(r・Y) = r・L_X(Y) for r∈R

L_Xはライプニッツ法則を満たす。
L_X(a・Y) = X(a)・Y + a・L_X(Y) for a∈A

R-線形性は明らかなので、示すべきはライプニッツ法則だけです。リー括弧のレベルでライプニッツ法則を書くと：

[X, a・Y] = X(a)・Y + a・[X, Y] for a∈A

これは定義に従った計算で示せます。念のため、計算を書いておきます。導分に対する関数によるスカラー乗法はドット、導分の結合と関数の積（可換環Aの積）は併置で表します。
b∈A に対して、

  [X, a・Y](b)
= (X(a・Y) - (a・Y)X)(b)
= (X(a・Y))(b) - ((a・Y)X)(b)

          (X(a・Y))(b)
        = X((a・Y)(b))
        = X(aY(b))
        = X(a)Y(b) + a(X(Y(b))
        = (X(a)・Y)(b) + (a・(XY))(b)

          ((a・Y)X)(b)
        = a(Y(X(b)))
        = (a・(YX))(b)

= (X(a)・Y)(b) + (a・(XY))(b) - (a・(YX))(b)
= ( X(a)・Y + a・(XY) - a・(YX) )(b)
= ( X(a)・Y + a・[X, Y] )(b)
まとめ
リー括弧 L:Der(A)×Der(A)→Der(A) に対して、右カリー化 L^∩ = L_(-) :Der(A)→[Der(A), Der(A)]_R がリー微分でした。左カリー化 ^∩L = L^(-) : Der(A)→[Der(A), Der(A)]_R でも同じことですが、左カリー化を Der(A)→Ω(A) $\otimes_A$ Der(A) とみなしたものを小文字ℓで書くことにします。ℓのライプニッツ法則は：

ℓ(a・X) = d(a) $\otimes$ X + a・ℓ(X)

と書けます。ℓは、本質的にはリー微分と何も変わりませんが、雰囲気としては外微分っぽくなります。
今回紹介した二項演算と左右のカリー化、その記法を表にまとめると：

二項演算右カリー化左カリー化

微分適用 D 方向微分 D_(-) 外微分 d

リー括弧 L リー微分 L_(-) 外微分風リー微分 ℓ

方向微分／外微分／リー微分／外微分風リー微分はいずれも、二項演算（双線形写像）をカリー化しただけの線形写像です。スカラー乗法の左右の違いとか、テンソル積か指数のどちらを使うか、などのどうでもいい差異から、様々な流儀や記法が（無駄に）派生しているだけです。