アミダのクイズ

アミダに関する問題を考えました*1。クイズとしてまーまー面白くて、理論上もある程度興味深い問題のように思えます。

アミダに関しては、「はじめての圏論 第7歩：アミダの圏」（これ単独で予備知識なしで読めます）で説明してます。次はアミダの例です。

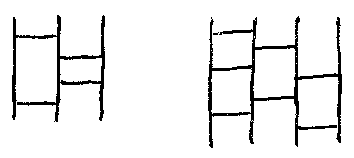
以下、アミダクジに使う図形であることを強調して（単にアミダではなくて）アミダ図と呼びます。

さて、アミダ図の横棒の数は、おおよそ、そのアミダ図の複雑さを表していますが、横棒の勘定を少し細工します。

1. 1番目の縦棒から（右に）出る横棒は、本数をそのまま勘定する。
2. 2番目の縦棒から出る横棒は、本数を2倍して勘定する。
3. 3番目の縦棒から出る横棒は、本数を3倍して勘定する。
4. 以下同様

このように勘定した横棒の総数（もちろん、単純な総本数ではない）を、そのアミダの重さと呼ぶことにします。例えば、

• 上の例の左のアミダ図の重さ= 2本 + 2本×2倍 = 6(本分)
• 上の例の右のアミダ図の重さ= 3本 + 2本×2倍 + 2本×3倍 = 13(本分)

2つのアミダ図A, B（縦棒の本数は同じ）があるとき、実際のアミダクジを行ってAとBで結果が変わらなければ、AとBは合同であると言うことにします。例えば、上の例の左のアミダ図は横棒がまったくない縦3本棒と合同です。

準備ができたので問題です。

1. 与えられたアミダ図に対して、それと合同で、できるだけ重さが小さいアミダ図を求めてください（実験をする）。
2. 与えられたアミダ図から、それと合同で重さが最小のアミダ図（それがもしあれば）を求める一般的なアルゴリズムを考えてください。

*1:ひらめいたわけではなくて、他の問題からの翻訳（言い換え）です。