「テンパリー/リーブ圏とカウフマンのスケイン関係式」で述べた状況は、もっと簡単な例でも確認できるので、簡単な例も紹介します。ブレイド図の代わりにアミダ図を使います。
アミダ図は、“あみだくじ”でお馴染みの次のような図です。
横棒の部分を次のように交差に置き換えると、ブレイド図と似た図形になります。
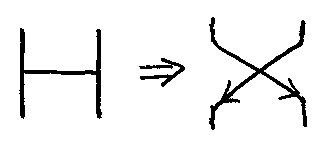
ブレイド図と違うのは、交差に上下(手前と奥)の区別がないので、一種類の交差しかないことです。この一種類の交差を適当に配置した図がアミダ図です。絵を描くときは、交差を横棒のまま描いてもかまいません。以下、交差をXで表すことにします。
アミダ図を上下に並べることで結合(composition)、左右に並べることでモノイド積を定義すると、アミダ図の全体は厳密モノイド圏(strict monoidal category)になります。この圏の対象は自然数の全体Nです。モノイド圏なので、紐(線)の伸縮や交替律(interchange law)による上下ズラシに起因する違いは無視します。
こうしてできた厳密モノイド圏を AmiDiag = (AmiDiag, , 0) とします。モノイド積
は、対象(自然数)では足し算で、射であるアミダ図では左右併置です。
「テンパリー/リーブ圏とカウフマンのスケイン関係式」ではブレイド図の圏BrDiagを使ったのですが、代わりにアミダ図の圏AmiDiagを使うと話が簡単になります。
ブレイド図のときと同じように、テンパリー/リーブ圏への線形表現を考えます。表現のターゲットとなるテンパリー/リーブ圏は、係数体をR、サークル乗数を-2にします。サークル乗数の選び方は「そうするとうまくいくから」です。複素数の計算は不要なので係数体は実数にしました(Qでもかまいません)。
線形表現 F:AmiDiag→TL(R, -2) は次のように定義します。
- F(1) = 1 (対象の生成元での値)
- F(X) = H + I2 (射の生成元での値)
Hは∪;∩のこと、I2はid2で縦の二本棒です。これだけ決めれば、あとはFが厳密モノイド関手であることから全域的に拡張できます。
アミダ図のあいだにも、(対称化した)ライデマイスター/アルチン同値関係〜RAを定義できて、この同値関係で割り算(ホムセットごとに商集合を作成)すれば、置換の圏Permと圏同値になります。AmiDiag/〜RA Perm。
上で定義した線形表現 F:AmiDiag→TL(R, -2) は、圏AmiDiag上の同値関係〜RAをイコールに移す(計算しましょう)ので、結果的に、置換の圏のテンパリー/リーブ線形表現 Perm→TL(R, -2) を与えます。
ブレイド図に関わる概念とアミダ図に関わる概念の対応関係は次のとおりです。
| ブレイド図 | アミダ図 | |
|---|---|---|
| モノイド圏 | BrDiag | AmiDiag |
| 圏の生成元 | B+とB- | Xだけ |
| 同値関係 | ライデマイスター/アルチン同値 | 対称化されたライデマイスター/アルチン同値 |
| 対応する群 | ブレイド群 | 置換群(対称群) |
| TLの係数体 | C | R |
| TLのサークル乗数 | 1 | -2 |
| スケイン関係式の係数 | ωとω' | 1と1 |
AmiDiagは簡単です。簡単な分、面白みに欠けるのですが、試したり遊んだりするときの負担が少ないのが良いと思います。