アミダくじによる場所(位置)の入れ替えは、置換を定義します。置換の全体を圏だと考えることができます。置換の圏を少し一般化して代入の圏を定義しましょう。一般化とは、「切れた線」と「枝分かれする線」を導入することです。単なる線(紐)だけではなく、印が付いたオダンゴを入れると、記号計算の枠組みとなる圏ができます。
内容:
アミダの圏と置換の圏
アミダの圏に関して僕は随分と色々書いています。
比較的まとまった説明は次の2つの記事(2006年)にあります。
2006年の記事だと、図形としてのアミダ図(Amida diagram)と、アミダ図により定義される置換(permutation)の区別が曖昧でした。「アミダのクイズ」あたりからはアミダ図と置換をハッキリ区別するようにしています(意図的に同一視することもありますが)。
以下の図は、アミダ図(の一部分)の変形操作を表しています。この変形で移りあえることにより、アミダ図の同値関係が導かれます。
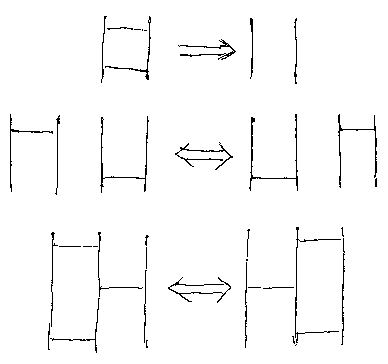
「圏のクリーネスター構成 -- エフイチに触発されて」から引用すると:
ブレイドの場合は、これらの関係式はアルチンの関係式です。結び目なら、一番目がライデマイスター移動II、三番目はライデマイスター移動IIIです。二番目は、モノイド圏の交替律を表現しています(スライディングとかシフティングと呼ばれることもあります)。ライデマイスター移動IIIは、ヤン・バクスター方程式とも呼ばれます。
アミダ図の圏をAmida、置換の圏をPermとすると、上記の同値関係で割る操作は Amida(n, n)→Perm(n, n) という写像を定義して、全体としては充満関手 Amida→Perm を定義します。
念のため、置換の圏Permについてまとめておくと:
- Permの対象は 0, 1, 2, ... という自然数である。
- Perm(n, n) は、集合 {1, 2, ..., n} の置換の全体である。
- n≠m のとき Perm(n, m) は空集合である。
- 恒等射は恒等置換(単位置換)、射の結合は置換の結合(合成)で与えられる。
Perm(n, n) はn次の置換群(対称群)です。なにもわざわざ圏にする必要もないようですが、そうではありません。圏の形にしておくと、Permを色々な形で一般化できます。アミダ図をブレイド(braid; 組み紐)図に置き換えると、ブレイドの圏ができます。ブレイド圏にトレースを導入すると、結び目(knot)、絡み目(link)、タングル(tangle; もつれ)などの議論ができます。
ブレイド圏にトレースを入れる話は次の記事を参照。
単純平面タングルの圏のデモに関しては次の記事に書いてあります。
代入の圏
置換の圏Permをブレイドとは別な方向で一般化してみます。
次の図は、Perm(3, 3) の射(3次の置換)の例を3つ挙げたものです。
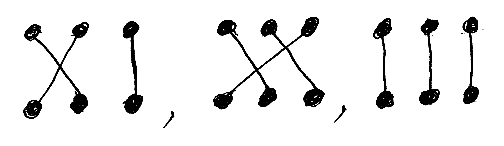
Perm(3, 2) は空集合(3→2 の射が存在しない)ですが、線が切れたり枝分かれするのを認めると、3→2 の射を考えることができます。次の図は、「切れた線」、「枝分かれ」を認めた“射”の例です。
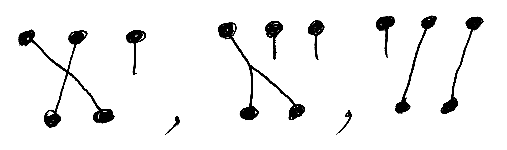
もう少しちゃんと説明しましょう。Permと似た圏Substを今から定義します。Substの対象はPermと同じく 0, 1, 2, ... という自然数です。自然数nを絵に描くときはn個の点を横に並べます。きれいに並ぶように横木も描くことにします。射は上から下に向かう何本かの線(紐)からなる図形です。
基本的な射として、I:1→1, X:2→2, !:1→0, Δ:1→2 を考えます。I, X, !, Δ は次のとおり。
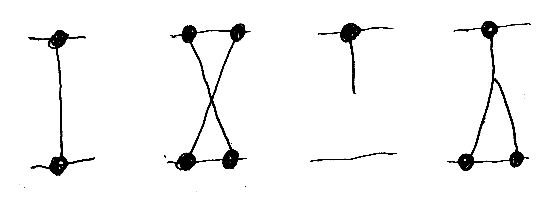
Iはid1です。Xはσとも書かれます。IとXだけをベースに、射を横に並べる操作(モノイド積)、縦に並べて繋ぐ操作(結合)を組み合わせるとAmida(図形的)またはPerm(組み合わせ的)ができます。IとX以外に、!を加えて作る圏は拡張アミダ圏と呼んだことがあります。
「僕がエフイチにハマる理由」より引用:
アミダのほうがブレイドより簡単な圏です。アミダの圏は恒等 I:1→1 と 入れ替え X:2→2 を元にして、結合(アミダを縦に繋ぐこと)とモノイド積(アミダを横に並べること)で生成した圏になります。これ以外に途中で切れた紐 !:1→0 (下図)を入れると、アミダより広い圏ができます。仮に拡張アミダ圏とでも呼びましょう。
1956年にティッツ(Tits)が夢想した「n次の一般線形群GLn(K)が、n次の対称群(置換群)になる」状況は、拡張アミダ圏で実現できます。つまり、拡張アミダ圏は、“足し算なしの線形代数”のモデルになっています。
今回さらに、Δを加えて圏を作ります。図形よりはむしろ組み合わせ的な特徴に注目して、代入の圏(category of substitutions)と呼びます。「代入」とはいっても、プログラミング言語の代入とは少し違います(無関係ではありませんが)。記号操作としての代入です。「置換」といったほうがふさわしいのですが、Permで既に「置換」(permutation)という言葉を使ってしまいました。
圏Substの射の表現方法
圏Substの任意の射は、I, X, !, Δ の組み合わせで表現できます。モノイド積を「×」、図式順結合を「;」とします。これらの記号で射を表現できます。先の図を再掲して、その後に記号表現。

- X×!
- Δ×!×!
- !×I×I
表現を簡略化するために次のような記号を導入することがあります。(詳しく説明しませんが、だいたい予想はつくでしょう。)
- In:n→n
- Xn,m:n+m→m+n
- !n:n→0
- Δn:n→n+n
いくつかの計算法則が成り立ちますが、ここでは割愛します。http://www.chimaira.org/docs/EtbDiagrams.htm (2004年)の「付録:いろいろな等式」に書いてあります(形がΔの逆向きの∇が使ってあるのでご注意)。
もっと端的にSubstの射を表現する方法には、f:n→m in Subst に、f*:{1, ..., m}→{1, ..., n} in Set を対応付けることです。基本的な射 I, X, !, Δ に関して、I*, X*, !*, Δ* を記述してみましょう。
f:n→m, g:m→k in Subst に対して、(f;g)* = g*;f* in Set となり、(-)* が反変関手になります。
上に挙げた3つの例を記述する関数 f1, f2, f3 : {1, 2}→{1, 2, 3} は次のようになります。
- f1(1) = 2, f1(2) = 1
- f2(1) = 1, f2(2) = 1
- f3(1) = 2, f3(2) = 3
さて、記号計算と関係付けるために、それらしい記法も導入します。代入(圏Substの射)を表す絵で、域(dom)と余域(cod)の点に名前を付けておきます。その名前を変数名だと思って、同時複数代入文(並列代入文)の形で射を表現します。次の例で練習しましょう。
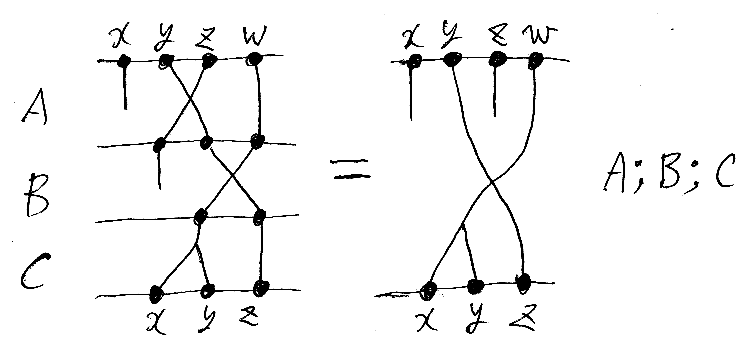
この絵は、A, B, Cという3つの射をこの順で結合することを表しています。点(ペグ(釘)とも呼びます)には、左から順に x, y, z, w と名前を付けることにします。最上段と最下段にしか名前が記入されてませんが、中間の横木上の点にも x, y, z と名づけます。
まず射Aに関して、上から下に向かって線(紐)を追いかけると、x→なし, y→y, z→x, w→z です。これを左右逆に書くと、{x←z, y←y, z←w} です。さらに、代入らしく「←」の代わりに「:=」を使いましょう。すると、A = {x := z, y := y, z := w} となります。B, Cも同じように書くと:
- B = {x := z, y := y}
- C = {x := x, y := x, z := y}
同時複数代入文の方向が右から左なので、反図式順結合記号を「・」として、結合に「・」を使ったほうが自然でしょう。結合の代入計算は次のように行います。
A;B;C
= C・B・A
= {x := x, y := x, z := y}・{x := z, y := y}・{x := z, y := y, z := w}
= {x := x, y := x, z := y}・({x := z, y := y}・{x := z, y := y, z := w})
= {x := x, y := x, z := y}・{x := w, y := y}
= {x := w, y := w, z := y}
{x := w, y := w, z := y} は、確かに絵の右辺と一致しています。
ランク付きアルファベット上の代入の圏
今導入した圏Substでは、射が「記号操作としての代入」とは言いながら、変数名の置き換えしかありません。これではツマラナイですね。そこで、定数記号や関数記号を付け加えてリッチな圏を作ります。付け加える記号の集合をアルファベットと呼びます。アルファベットは習慣によりΣで表します(総和記号ではないので注意してください)。アルファベットΣに定数記号や関数記号が含まれます。
アルファベットに入るべき記号を絵で描くと、次のような形をしています。
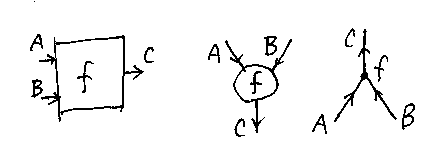
「自己関手の圏とモナド」から図の説明を引用すると:
左の図は、fを箱で描いているのでボックス図と呼びます。ほんとはボックス&ワイヤー図なんだけど、主役は箱でワイヤーは箱から出る端子(コネクタ、ピン)を示すだけ。
まんなかの図は、「バエズとステイのロゼッタストーン論文と現代のヒエログリフ」で紹介した論文で使われています。箱の代わりに丸、方向は左から右じゃなくて上から下です。
物理では、上から下より下から上に描くほうが多数派です。右の絵は、下から上の方向で描いています。そして、fを表す丸は点に退化してます。これはもう、物理のファインマン図ですね。
今回は、関数記号fに入出力の“型”は不要で、引数の個数に相当する数だけを問題にします。引数の個数はランクとかアリティと呼びます。集合Σには、rank:Σ→{0, 1, 2, ...} というランク関数(アリティ関数)が付随しています。(Σ, rank) をランク付きアルファベット(ranked alphabet)と呼びます。f∈Σ で、rank(f) = n のとき、fは n→1 というプロファイルの射だと考えます。
実例を出したほうが早いでしょう; Σ = {c, f, g} で、rank(c) = 0, rank(f) = 1, rank(g) = 2 とします。Σの記号を射に加えた代入の圏を Subst[Σ] とすると、Subst[Σ] のなかで、c, f, gは次のような射となります。
- c:0→1
- f:1→1
- g:2→1
次の図は、c, f, gを含んだ組み合わせの一例です。
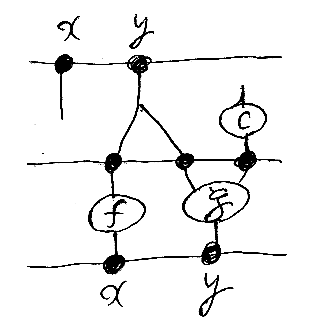
上段と下段の分けて、それぞれを複数同時代入文の形で表現してみると:
- {x := y, y := y, z := c} : 2→3
- {x := f(x), y := g(y, z)} : 3→2
結合の代入計算は次のようになります。
{x := f(x), y := g(y, z)}・{x := y, y := y, z := c}
= {x := f(y), y := g(y, c)}
これだと確かに代入計算している感じがするでしょ。
圏Subst[Σ]のなかには、x, yのような変数名はホントには登場しません。それは、変数は事実上ラムダ束縛されているので、アルファ変換で自由にリネーム可能だからです。自由にリネーム可能とは名前自身に意味はなくて、番号でもよいことになります。だから、Subst[Σ] の対象は自然数(個数や番号を表す)なのです。
Subst[Σ] のΣを変えると、それに応じて圏が変わります。ランク付きアルファベットの圏(Σ達が所属する圏)を考えると、Substは、ランク付きアルファベットの圏をベースの圏とするインデックス付き圏になっています。Σ→Σ' をランクを保存する写像だとすると、リダクト関手 Subst[Σ']→Subst[Σ] が誘導されます。さらには、Subst[-]は項構成関手(term forming functor)でもあり、適当な圏の上のモナドと解釈できます。
とまー、点と線(紐とペグ)を並べたり繋いだりから出発して、たいていの記号計算ができるような圏を構成できます。Subst[Σ]は、Σから構成される項代数(term algebra)の一般化で項圏(term category)とでも呼ぶべきものです。項代数(の台集合)は、ホムセットSubst[Σ](0, 1) として得られます。Subst[Σ] からの(例えばSetへの)関手は、記号計算の意味論を与えるとみなせます。
インデックス付き圏(あるいはモナド)Subst[-]を使ってエルブランモデルを作ったりすると楽しいのですが、その話はまたの機会に。