先ほど書いた「関手と自然変換:コゥゼンの記号法」より:
絵算派の僕としては、以上のことは、2-圏や二重圏の交替律(interchange law)をグロービュラー図/タイル図に描けば明らかな事実なので「そりゃそうだろう」とも思うのです
気になるので書いておきます。でもごく短い説明だけ。
二重圏(double category)というのは、対象(0-セル)と水平射(水平1-セル)と垂直射(垂直1-セル)、それと2-セルからなる高次圏(higher category)の一種です。二重圏の典型的な例はコボルディズムの圏ですが、計算に関係する例では、状態遷移系を水平射として、次のような二重圏が考えられます。
- 対象:開始状態または終了状態の集合
- 水平射:状態遷移系
- 垂直射:開始状態または終了状態の集合のあいだの写像
- 2-セル:状態遷移系のあいだの模倣関係
二重圏には次の演算が備わっています。
- 水平射の結合 (水平1セルの横結合)
- 垂直射の結合 (垂直1セルの縦結合)
- 2-セルの横結合
- 2-セルの縦結合
演算記号を考えるのがすごく面倒です。適宜オーバーロードすることになりますが、オーバーロードをやり過ぎると分かりにくくなります。とりあえず、次の記号を使うことにします。
- 水平射の結合 -- 「;」(後で使わないけど)
- 垂直射の結合 -- 「;」(オーバーロード、後で使わないけど)
- 2-セルの横結合 -- 「;;」
- 2-セルの縦結合 -- 「|」
順序は図式順です。
さて、二重圏における交替律(interchange law)を絵で描くと次のような感じです。
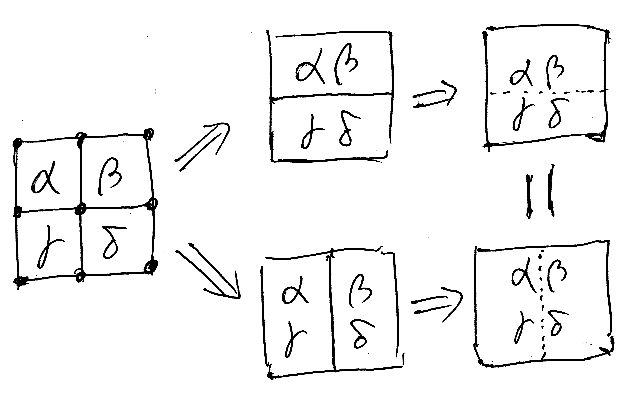
先に定義した記号を使ってテキスト表記で書くと:
- (α;;β)|(γ;;δ) = (α|γ);;(β|δ)
二重圏の垂直射を恒等射だけに限定してしまうと2-圏になります(定義の強弱の話は棚上げ)。図で言うと、縦の辺が一点に潰れてしまうことです。潰れた図でも交替律は成立して、それが2-圏の交替律となります。下の図の上段が垂直射が潰れる絵です。
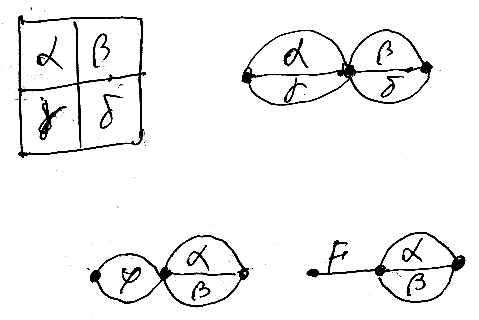
図の下段は、2-セルが1-セルに潰れる絵です。φは2-セルですが、φとして特に水平射Fの恒等2-セルをとると、面が線につぶれます。「対象」と「対象の恒等射」を同一視するのと同じように、「射(1-セル)」と「射の恒等2-セル」を同一視すると、射と2-セルの横結合が定義できます。このような退化した状況で交替律を書き下すと、それが分配律になります。2-圏をもっと退化させるとモノイド圏になります。
以上のことから、高次圏における分配律は交替律の特殊なモノとも言えるし、(同じ事だが)交替律は分配律の一般化とも言えます。図形的には、縦と横の交換可能性、2次元の等方性(一様性)の表現です。これは、小学校で習った次のような事実の高次圏論的な主張ですね。
- 方眼紙の升目の個数を勘定して長方形の面積を求めるとき、数える順番によらずに同じ値となる。