アクセス権限チェックを、モナドとコモナドで定式化してみる

http://twitter.com/ckuwata/status/3323599917 ：

ログインチェックやリクエストトークンとか、セキュリティ関連の処理を後付けするのにモナドが使えそうな気配はするんだがなあ。

臭覚がだんだん鋭くなってきたかな？ :-) こりゃモナドっぽい香りがしてますよね。

このテのハナシはとてもいい例題になります。でも、モナドだけじゃちょっと無理で、コモナドも使いましょう。ラッピングの手法を使うと分かりやすいです。やってみましょう。

[追記 date="2009-08-18 (翌日)"]読みやすくなるように、少しだけ文言を修正・追加しました。[/追記]

内容：

基礎となる圏

話を簡単にするために、基礎となる圏Cは、射が写像（関数）である圏とします。f:X→Y は、写像fの始域が集合X、fの終域が集合Yである*1ことを示します。とりあえずは、このような仮定で話を進めます。しかし、射が写像（関数）であるという仮定は本質的ではなくて、Cがある程度タチが良い圏なら同じ議論が通用します。

最初に老婆心からの注意を述べておきます； Cの射の一部分を素材に、新しい圏Dを作ったとき、f∈C に対して、Dにおける dom(f) が集合とは限りません。仮に dom(f) が集合であっても、それが「写像fの始域＝Cにおける域」とも限りません。例えば、固定されたAに対して、f:X×A→Y×A という形の写像だけを集めてDとして、D.dom(f) = X, D.dom(f) = Y と決めてもかまいません； D.dom, D.cod は、（Cじゃなくて）Dのdomとcodです。

僕が口癖のようにいつも言っている「先入観や思いこみで決めつけるのは止めましょう、公理さえ満たせば何だっていいんですよ」の例です*2。これ以上詳しくは説明しませんが、圏としての域（dom）、余域（cod）に疑問を感じたら、今の注意を思い起こしてください*3。

認可トークン

認可トークンとは、アクセス権限を表すデータ／値です。以下では、単にトークンとも言います。トークンtは、アクセス権限を表すので、「アクセス権限 t」のように言ってしまうこともあります。

認可トークン全体の集合をTとします。ホテルのマスターキーに当たるトークンを t0 と書き、マスタートークンと呼びます。t0 は万能の合い鍵です。現実には、マスタートークンがあるととてもヤバイですが、理論上はマスタートークンがあるとみなします。

チェッカー

Cの射fごとに、c[f] という射が割り当ててあるとします。c[f] をfのチェッカーと呼びましょう。B = {true, false} を真偽値として、f:X→Y ならば、c[f]:X×T→B という形をしています。

c[f](x, t) の意味は：

• アクセス権限tのもとで、引数xに対して操作fが許されるなら true
• そうでないなら false

ということです。

ラッピング

ラッピングとは、Adapterデザインパターンを圏論のなかで焼き直した手法です。射f自身には手を加えず機能を後付けしたり、インターフェース（domとcod）を変更したりします。これは、コンポネント作成者には負担をかけず、「トランスレータ and/or ランタイムエンジンで頑張る」方法です*4。

c[f]を使って f:X→Y をラップしましょう。準備として、β_Y:Y×B→Y_⊥を次のように定義します。

• β_Y(y, true) = y
• β_Y(y, false) = ⊥

⊥（ボトム）は、「エラー、未定義、例外」などを表す記号で、Y_⊥ はYに⊥を付け加えた集合です。また、Δ_X(x) = (x, x) は集合Xの対角写像とします。

ではラッピングの定義を与えます； f:X→Y をラップした結果f'は、f':X×T→Y_⊥ となります。

• 定義： f' = (Δ_X×T);(f×c[f]);β_Y

上の定義はやや不正確な（割愛した）ところがあるので、露骨な定義を追っていくと：

1. (Δ_X×T)(x, t) = (Δ_X(x), id_T(t)) = ((x, x), t)
2. ((x, x), t) = (x, x, t) = (x, (x, t)) （ここを割愛）
3. (f×c[f])(x, (x, t)) = (f(x), c[f](x, t))
4. f'(x, t) = if (c[f](x, t)) then f(x) else ⊥

JavaScript風に書くならば：

function f'(x, t) {
 if (c[f](x, t)) {
  // チェック成功
  return f(x);
 } else {
  // チェック失敗
  throw ⊥;
 }
}

絵図は自分で描いてみてください。

アンラッピング

アンラッピングは、ラッピングによって得られた射からもとの射を再現する手続きです。いつでもアンラップできるわけではないし、それが必要とも限りませんが、アンラップができれば色々と便利です。

g:X×T→Y_⊥が次の条件を満たすとします。

• 任意のx∈X に対して、g(x, t0) ≠ ⊥ （t0はマスタートークン）

さて、f:X→Y に対して、g = f' として得られたgはこの条件を満たします。gが上記条件を満たすとき、g(x, t0) の終域をYに狭めることができます。そこで、gに対して `g を次のように定義します。

• `gは、(x|→g(x, t0)) の終域をYに狭めた写像

すると、次が成立します。

• `(f') = f

露骨に書けば：

• f'(x, t0) = if (c[f](x, t0)) then f(x) else ⊥ = f(x)

t0がマスタートークンなので、このようなことが出来るのです。

ラッピング／アンラッピングへの補足

「モニャドセミナー4の予定：訂正と補足」に、「ラッピング関手／ラッピング半関手」というような言葉使いがまずい、と書きましたが、神経質過ぎた気がします。

ラッピングを定義した段階では、それが関手であることが分かりにくいことがあります。とりあえず関手でなくてもちゃんと役に立つのです。アンラッピングのほうは、関手である必要はほとんどありません。そこで、一般的には「ラッピング対応」と呼ぶべきだと言ったのですが、事後的にでも関手であることが分かっているなら、「ラッピング関手」と呼んで悪いことはないですね。

今回のラッピング対応 f|→f' は、このままでは関手ではありません。しかし、結果的に両クライスリ圏への関手になっています。別な言い方をすると、ラッピング対応を使って両クライスリ圏への関手を構成するのです。

Maybeモナドと対角コモナド

A|→A_⊥ という対応は、モナドの関手部分になっています。モナド乗法 (A_⊥)_⊥ → A_⊥ は、2個のボトムを同一視する写像で与えられます。モナド単位は、AをA_⊥ に埋め込む写像です。これは、Maybeモナドとして知られていますが、例外機構の一番単純な定式化になっています。

Maybeモナドは、実はモノイダル・スタンピング・モナドです。m: {⊥} + {⊥} → {⊥} を重ね合わせ写像（fold map）、u:0→{⊥} を空集合の埋め込み写像とすると、({⊥}, m, u) は、mを乗法、uを単位とするモノイドです。ただし、直積の代わりに直和を考えてのモノイドですが。このモノイドを直和でスタンピングしたものがMaybeモナドです。

さて一方、対角写像 Δ_V:V→V×V は、余乗法（乗法の双対概念）を定義し、なんでもかんでも1点に写す写像 !_V:V→1 と共にコモノイドとなります。この対角コモノイドを直積でスタンピングすればコモノイダル・スタンピング・コモナドが得られます、それが対角コモナドです。

モノイド、コモノイドのスタンピングで、それぞれモナド、コモナドが得られることは絵算で簡単に示すことができます。このとき、圏の掛け算（モノイド積）が何であるかはどうでもいいので、直積スタンピングでも直和スタンピングでも通用する話です。現に、Maybeモナドは直和スタンピング、対角コモナドは直積スタンピングで構成されています。

両クライスリ射とアクセス権限チェック

Fがモナドの関手部分のとき、f:X→F(Y) の形の射がクライスリ射でした。もうひとつのクライスリ射 g:Y→F(Z) があるとして、このままでは「fとgの結合」を作れません。が、モナド乗法を使って細工すると、f:X→F(Y) と g:Y→F(Z) の新しい結合 f#g :X→F(Z) が作れて、この結合 # に関して圏を構成できます。それがクライスリ圏でした。

図：Mによるモノイダル・スタンピング・モナドの場合のクライスリ結合

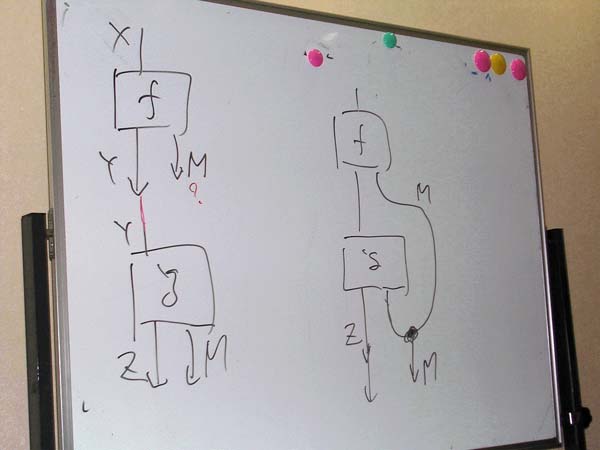
まったく同様に（双対的に）、Gがコモナドの関手部分のとき、f:G(X)→Y の形の射が余クライスリ射で、余クライスリ射の余クライスリ結合に関して余クライスリ圏を構成できます。

Maybeモナド（例外モナド）に関しては、クライスリ射 f:X→Y_⊥ は、例外を起こすかも知れない関数です。そして、例外を考慮した結合がクライスリ結合ね。対角コモナドに関して言えば、余クライスリ射 f:X×V→Y は、値がVに入る非ローカル変数を参照する関数です。非ローカル変数を変更せずに引き回す結合が余クライスリ結合です。

さてここで、f:X→Y をラップした関数 f' の形を思い出しましょう。

• f' : X×T → Y_⊥

余域は、Maybeモナド（例外モナド）で修飾され、域はトークン領域Tによる対角コモナドで修飾されています。つまりこれ、クライスリ射であると同時に余クライスリ射でもあるのです。僕は、このテの射を両クライスリ射と呼んでいます（「両」じゃなくて「双」を使う前例があるようです via 酒井さん）。

両クライスリ圏を一般的に構成することもできますが、今扱っている例では、大道具を使わなくても手作業でチマチマいじくり回して、両クライスリ結合と両クライスリ圏を構成できます。

圏Cの、MaybeモナドとT-対角コモナドに関する両クライスリ圏をDとしましょう。両クライスリ圏の作り方から、|C| = |D| で、対象類は同じです。f:X→Y in C に対して、

• W(X) = X in D, W(Y) = Y in D
• W(f) = f' = (fのラッピング)

とすると、Wは関手になっています。W(f)がちょうど、fに対してアクセス権限チェックを追加したものになっています。

まとめ

最後のほうは筋書きを示しただけですが、細部を自分で埋めることは、モナド／コモナドのとても良い練習問題だと思います。モナド／コモナドとは言っても、スタンピングしか使ってないので、計算が複雑になることはありません。

ただし、モナドが直和スタンピング、コモナドが直積スタンピングなので、直積だけ（あるいは直和だけ）のケースよりはちょっと難しいです。一部、絵算が使いにくい箇所があるので、そこは等式計算で乗り切りましょう。

実感を得るには、お好みのプログラミング言語で、サンプルコードを書いてみるといいと思います。モナド／コモナドがいつものプログラミング（everyday programming）のなかにも潜在していることが分かるでしょう。

クライスリ構成を繰り返し適用したり、複数のモナド／コモナド達を一度に扱うには、もう少し進んだ話（モッギモッジのテンソル強度、ベックの分配法則、indexed categoryのグロタンディーク平坦化、…）が必要ですが、これらウルトラ・アブストラクトに思える概念も、今なにげなく書いているその平凡なコードのなかにも、ほら、ひそんでいますよ。

*1:域、始域などの言葉を整理できたことは、「層・圏・トポス」合宿の成果です :-)

*2:次のような規則や条件はどこにもないのです； 「射fが写像であるとき、圏論的な「fの域」は、集合論的な「fの始域」でなくてはならない」。勝手な規則や条件をでっち上げてはいけません。

*3:くどいけど、もう一回いっておくと： 類推は大事で、記憶の節約になり、発見につながることもあります。しかし、典型からの類推を根拠なしに適用するのはやめましょうね、ホントに！

*4:ソフトウェアのラッピングには、静的ラッピングと動的ラッピング、それらの併用があります。具体的手法には、継承、委譲、高階関数などがありますが、やろうとしている本質的な内容に変わりはありません。