「Webサービスを設計するための単純明快な方法」や「Webサービスの設計:Webの状態遷移図の描き方」で、Webにおける状態遷移の図を示しました。もう少し図の描き方について考えます。そして、それらの図がいったい何を意味するかにも触れます。
内容:
アクション、ハイパーオブジェクト=状態、モジュール=サブシステム
まず図の描き方の復習をしましょう。サーバー側の処理であるアクションは小さめの黒丸で表します。アクションのレスポンスとして返されるハイパーオブジェクトは大きめの白丸です。ハイパーオブジェクトはクライアント側の状態と解釈され、リクエストを発行するボタンであるトリガーを持ちます(トリガーが必須ではありませんが)。
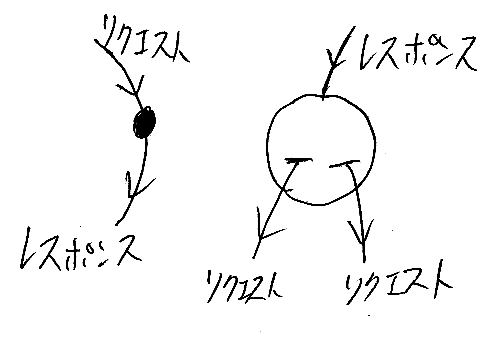
いくつかのアクションとハイパーオブジェクト(=状態)のノード達は互いに繋がれて、メッセージングと状態遷移のフローを形成します。ノードを辺で繋ぐときには、リクエスト辺はリクエスト辺と、レスポンス辺はレスポンス辺と繋ぎます。もちろん、辺の方向も合わせないとダメです。実際には、リクエストもレスポンスもデータ型(メディアタイプとスキーマで定義される)を持ちますから、データ型も一致しないと繋げません。でも煩雑になるので、今回はデータ型はいちいち明示しません。
一群のノードと有向辺は有向グラフを作りますが、これらをひとまとまりのモノとして把握するために、四角い枠線で囲みます。そうやって作られた四角をとりあえずモジュールと呼ぶことにします。モジュールは、Webサービス・システムの一部分、つまりサブシステムを構成することになります。次の図はモジュールの例です。「ログイン成功したらマイページを表示する」のような流れを想定しています。
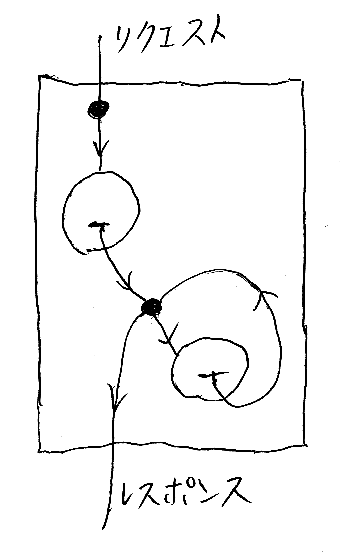
モジュールの図示
モジュールには、たいていリクエストかレスポンス(あるいは両方)が入り込みます。また、リクエストかレスポンスが出て行くことになります*1。要するに入り口と出口があるよ、ってことです。そこで「入り口 → 出口」をどういう方向で描くかって大問題が発生します。なんだかんだと悩みたくないので、方向は上から下、上が入り口、下が出口と決めます。断固決めます。
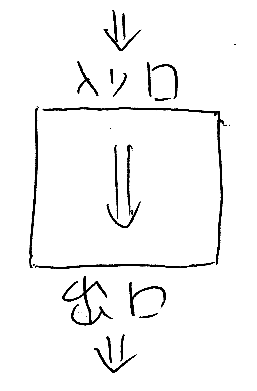
一番簡単なモジュールは、アクションかハイパーオブジェクト(状態)を1個だけ含むものでしょう。それらの中身を描いている時(図の上のほう)はいいのですが、中身を隠してしまう(図の下のほう)とちょっとした問題があります。
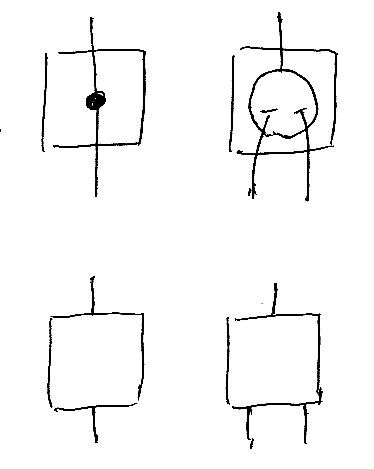
グラフの有向辺がリクエストかレスポンスか区別が付かないのです。ヨクワカラン図ですね。もっと大きなモジュールでも同じ問題が起きます(そして図が大きいとより深刻です)。点線を使うとか辺に色を付けるとかの方法もありますが、実際に描いてみるとメンドクサイ! そこで次の対策をします。
- メッセージの入り口である四角形上部を左右に分けて、左をリクエストの入り口、右をレスポンスの入り口とする。
- メッセージの出口である四角形下部を左右に分けて、左をレスポンスの出口、右をリクエストの出口とする。
念のために、リクエストとレスポンスを識別するマークも決めておきます、リクエストはR、…… ダメだ、どっちもRだ。ウーンと、リクエスト(reQuest)はQ、レスポンス(reSponse)はSとしましょう。このような約束事を設けて、実線だけでもリクエストとレスポンスの区別が付くようにします。
って書いておきながら、下の図では「R」だよっ。ウーム。僕、スキャン画像を修正するツール持ってないのよね。ごめんなさい、RはSに読み替えて。
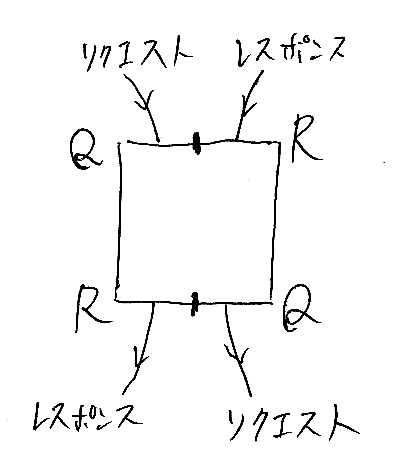
いいことありそうだ
今、とあるWebサーバーAがあったとします。このサーバーAは、Webクライアントからのリクエスト(略称Q)を受けて、レスポンス(略称S)を返すのですが、他のサーバーBが提供するWeb APIを呼び出すとします。つまり、サーバーAはBに対してはクライアントとなります。この状況を図示すると次のようです。(文字RはSに読み替えてください。レスポンスのことですね。)
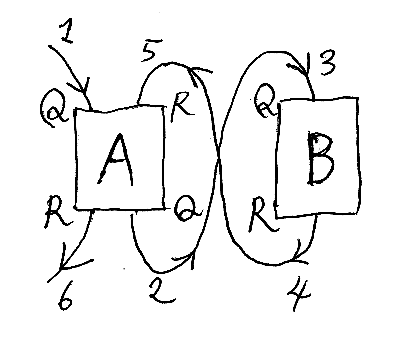
- クライアントからのリクエストがAに入ります。
- サーバーAがサーバーBにリクエストを送ります。
- サーバーAからのリクエストがBに入ります。
- サーバーBがレスポンスを返します。
- サーバーBからのレスポンスがAに入ります。
- サーバーAがクライアントにレスポンスを返します。
AとBが8の字形にワイヤー(有向辺)で繋がることに注目してください。この8の字繋ぎは、一般のモジュールを繋ぐときにも使えます。
[追記] 注意:ここから先は引いちゃう人がいるかもしれない。無理して読まなくてもいいし、流し読みして忘れてもらってけっこうです。[/追記]
さてここで、次の図を見てください。
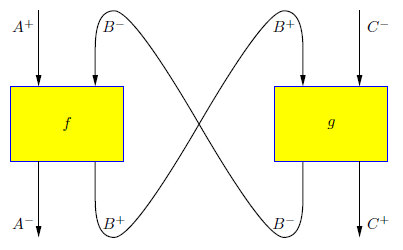
8の字形の結合ですね。この図はサムソン・アブラムスキーのスライドだか論文(出典不明、調べれば分かると思うが)からコピーしたものです。そして次は、白旗優 (Shirahata, Masaru)さんの論文 "Geometry of Interaction explained" (http://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/43041/1/1318_19.pdf) にあった図です。
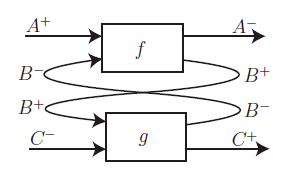
アブラムスキーが上から下なのに対して、白旗さんは左から右の方向を採用してます。先に述べたように、僕はアブラムスキーと同じ方向「上から下」を採用します。
アブラムスキーや白旗さんが扱っている話題は、コンパクト閉圏(compact closed category)とGoI構成(Geometry-of-Interaction construction)です。僕自身も随分と前からコンパクト閉圏やGoI構成を利用してやろうとたくらんでいました。
Webのメッセージフロー(リクエストとレスポンスの流れ)をうまいこと図示すると、結果的にトレース付きモノイド圏やコンパクト閉圏になるのです。もう少し正確にいうと、メッセージの直列結合と直和とルーピングによりトレース付きモノイド圏(traced (symmetric) monoidal category)ができて、そのGoI構成(Int構成ともいう)によりコンパクト閉圏ができます。
「Webサービスの設計:Webの状態遷移図の描き方」の最後で次のように言いました。
ともあれ、「図式化すればいいことありそうだ」と僕は思ってますが、もっと経験を積まないとホントのところは何とも言えません。とりあえずは、状態遷移図をイッパイ描いてみることからスタートですね。
トレース付きモノイド圏やコンパクト閉圏、つまり圏論的フローチャートの議論が使えるのが「いいこと」のひとつです。
フローチャートや副作用のような“嫌われ者”を、僕は「いいこと」に含めているのですが、そのへんの事情は次の記事とそこからのリンクをだとってみてください。
特にフローチャートについては:
*1:入る辺、出る辺もなくても別にかまいません。それが無意味でもありません。