このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

エディントンのイプシロンを圏論的に定義する

雑記／備忘

「組み合わせ的主バンドル： エディントン・バンドル」の続きというか追記というか、関連する話。

対称群が作用する組み合わせ的な主バンドルが「なんか面白な」と思ったので紹介したのですが、エディントンのイプシロンを定義するだけなら、バンドル構造を経由しないでもっと直接的な定義が可能です。適当なセッティングのもとで、エディントンのイプシロンは厳密モノイド圏のあいだの関手になります。

内容：

有限骨格圏

有限集合と写像の圏をFinSetとします。FinSetの骨格（skeleton）となるような圏を作ります。圏の骨格については、「骨格的な圏と圏の骨格」で書いています。念のために繰り返しておくと； Cの部分圏Dが、Cの骨格だとは：

  1. Dの同型は恒等射だけである。
  2. Cの任意の対象は、Dの適当な対象と同型である。
  3. Dは充満部分圏である。つまり、D(A, B) = C(A, B)。

骨格概念をわずかに拡張して、DがCの外にあっても、埋め込み関手 J:D→C があって、Jの像である圏 J(D)⊆C が上記の意味で骨格なら、DはCの骨格と呼ぶことにします。そして、FinSetの骨格となるような圏（と埋め込み関手の組）を有限骨格圏（finite skeleton category）と呼ぶことにします。

まず、ほぼ自明な有限骨格圏FinSkelを作ります。{1, 2, ..., n} = {i∈N | 1≦ i ≦n} を[n]と略記します。

  • |FinSkel| = N = {0, 1, 2, ...}
  • FinSkel(n, m) := FinSet([n], [m])
  • 射の結合は写像の結合とする。
  • 恒等射は恒等写像とする。

対象を（集合ではなく）自然数にしたのは記述や取り扱いが容易になるからです。埋め込み関手 J:FinSkel→FinSet を、J(n) = [n] で定義すれば、埋め込みの像はFinSetの部分圏として骨格になります。

「組み合わせ的主バンドル： エディントン・バンドル」で出てきた各種の写像の集合は、有限骨格圏FinSkelの一部として説明できます。

  • Map(p, n) := HomFinSkel(p, n) = FinSkel(p, n)
  • Inj(p, n) := MonFinSkel(p, n) （モノ射の集合）
  • Bij(p, p) := IsoFinSkel(p, p) （同型射の集合）
  • S(p) := AutFinSkel(p) （自己同型射の群）

有限骨格圏のモノイド構造

FinSkelに対称モノイド構造を入れましょう。

  • 対象n, mに対して、n\oplusm := n + m （自然数の足し算）
  • f:n→m, g:p→q に対して、f\oplusg:n\oplusp→m\oplusq は：
    • (f\oplusg)(i) = f(i) if (1≦i≦n)
    • (f\oplusg)(n + j) = n + g(j) if (1≦j≦p)
  • 0が単位対象
  • 対称σは：
    • σn,m(i) = n + i if (0≦i≦n)
    • σn,m(n + j) = j if (0≦j≦m)

今入れたモノイド構造は厳密（strict）です（この「厳密」の意味は、モノイド法則が等式で成立している、ということです）。モノイド積\oplusは、FinSetにおける直和と同じですが、FinSetの直和は厳密モノイド積にはなりません。対象を自然数にしているので、モノイド積が厳密モノイド積になります。

モノイド積を持ったFinSkelは、「PROと代数系 -- toward 量子と古典の物理と幾何＠名古屋」で述べたPRO／PROPになっています。

FinSkelの同型射だけを取り出した圏Iso(FinSkel)は、すべての対称群S(n)を寄せ集めた構造をしています。S(n)の集まりであるIso(FinSkel)も対称モノイド圏になっています。

  • Iso(FinSkel)(n, n) = IsoFinSkel(n, n) = AutFinSkel(n) = S(n)

FinSkelのモノ射だけを取り出した圏Mon(FinSkel)もまたFinSkelの部分モノイド圏となります。

圏の生成系と関係

有限骨格圏FinSkel（と同型な圏）を、生成系と関係（generators and relations）で定義してみます。ここで扱う圏は、PRO（Nを対象とするモノイド圏）に限定します。したがって、対象の集合と対象のモノイド積は先に決まっています。これに対して、有限個の生成射（generating morphism）と等式系（system of equations）として与えられる関係で圏を定義します。

ここで使う生成系は、I（大文字アイ）、X（大文字エックス）、Y（大文字ワイ）、.（ピリオド）です。

  1. dom(I) = cod(I) = 1
  2. dom(X) = cod(X) = 2
  3. dom(Y) = 2, cod(Y) = 1
  4. dom(.) = 0, cod(.) = 1

これらの記号的射から自由に生成された圏を作ります。Iはid1なので組み込みと考えて、残りの3つの記号が生成系Σを形成するとします。Σ = {X:2→2, Y:2→1, .:0→1}。

生成系（指標とも呼ぶ）Σから自由に作ったPROをFreePRO(Σ) とします。FreePRO(Σ)は、ある種の図式の圏とも記号列の圏とも考えられます。この点を説明すると長く退屈になるので、1個の絵で済ませます。

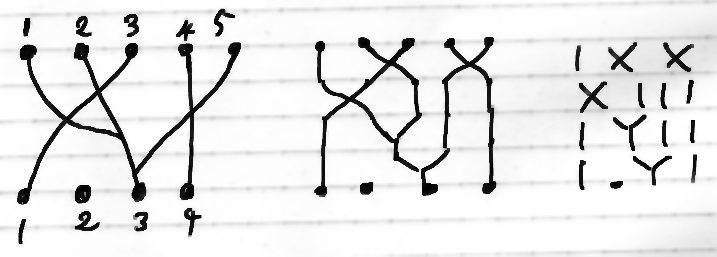
いちばん左側の絵は、ドットの列を繋ぐワイヤーの図式です（向きは上から下）。ワイヤーの交差と合流を許します。上側のドットからは必ずワイヤーが出ている必要がありますが、下側のドットが“空き”でもかまいません。

ワイヤーの図を適当に整理して、{I, X, Y, .}の2次元並びに整形できます。横の並びは単なる併置、縦の並びは';'（セミコロン）で区切ることにすると、図の右側は IXX;XIII;IYII;I.YI という文字列表現を持ちます。セミコロンで切って縦に並べるとだいたい絵を再現できます。

FreePRO(Σ)の射を図形的に解釈・表現すれば、ワイヤーの図式（ダイアグラム）だし、形式言語的に解釈・表現すればアルファベット集合{I, X, Y, .}から併置とセミコロン区切り連接で生成された文字列です。ワイヤー図式や文字列は、厳密モノイド圏の公理に従って同一視されます。例えば、XII;IIX = XX です（交替律による）。

厳密モノイド圏の公理以外に：

  • Xに関してライデマイスター／アルチン同値関係を入れる。
    • X;X = ||
    • X|;|X;X| = |X;X|;|X
  • Yと.（ピリオド）には結合律、左単位律、右単位律を入れる。
    • Y|;Y = |Y;Y
    • .|;Y = I
    • |.;Y = I

また、Xを何個か組み合わせることにより対称σn,mを作り、対称モノイド圏にします。

FreePRO(Σ)を、今ザッと述べた関係達（けっこうたくさんある）で割り算して商圏を作ると、有限骨格圏FinSkelと同型になります。別な言い方をすると、生成系 Σ = {X, Y, .} と圏の同値関係が、FinSkelの表現（プレゼンテーション）になっています。

なお、FreePRO(Σ)からFinSkelへの標準的な関手（射影関手） P:FreePRO(Σ)→FinSkel は次で与えられます。

  • P(I) = (1|→1) = id1
  • P(X) = (1|→2, 2|→1) = σ1,1
  • P(Y) = (1|→1, 2|→1)
  • P(.) = 空集合[0]から[1]への唯一の写像

エディントンのイプシロンの定義

M = {-1, 0, 1} とします。Mは掛け算でモノイドになります。必要があれば、Mはモノイドだと考えることにします。

エディントンのイプシロンを、有限骨格圏FinSkelの射の集合Mor(FinSkel)からMへの写像として定義します。

  • ε:Mor(FinSkel)→M

εを定義するために、まず Φ:Mor(FreePRO(Σ))→M を定義します。このΦが次の性質を持つなら、Mor(FinSkel)上の写像が決まること（well-defined）になります。

  • f, g∈Mor(FreePRO(Σ)) に対して、fとgが同値なら Φ(f) = Φ(g)

具体的にΦは次のように定義されます。

  • Φ(I) = 1
  • Φ(X) = -1
  • Φ(Y) = 0
  • Φ(.) = 1

圏の結合とモノイド積に関しては：

  • Φ(f;g) = Φ(f)・Φ(g)
  • Φ(f\oplusg) = Φ(f)・Φ(g)

つまり、結合もモノイド積もMの掛け算に移ります。この定義が、同値関係と協調することを示さないとダメなんですが、面倒で退屈なんで割愛します。

上記のルールに従った計算例を出すと：

   Φ(IXX;XIII;IYII;I.YI)
 = Φ(IXX)・Φ(XIII)Φ・(IYII)・Φ(I.YI)
 = (1・-1・-1)・(-1・1・1・1)・(1・0・1・1)・(1・1・0・1)
 = 1・-1・0・0
 = 0

すぐに分かるように、Yが1個でも出現すればΦの値は0になります。また、Xが奇数個出現すると(-1)になります。まとめると：

  1. Yが1個でも出現すれば 0
  2. Xの出現個数が偶数（0も含む）ならば 1
  3. Xの出現個数が奇数ならば -1

実は、この定義は置換に対する符号の定義と同じ方法を使っています。置換の符号は、置換の転倒数だけ(-1)を掛け算するのですが、置換の転倒数の偶奇はXの出現個数（互換の出現個数）の偶奇と同じです。このことから、エディントンのイプシロンは置換の符号の直接の拡張だと分かります。

モノイド関手としてのエディントンのイプシロン

エディントンのイプシロンを、ε:Mor(FinSkel)→M という写像として定義しましたが、εやそのもとになるΦは関手と考えられます。いや待て、そもそもMが圏になってないのでは？

まずは M = {-1, 0, 1} を圏とみなすことから始めます。Mは掛け算に関してモノイドなので、単一のダミー対象を持つ圏と考えることができます。圏としてのMは次のように定義されます。

  • |M| = {*} （*はダミー対象）
  • M(*, *) = {-1, 0, 1}
  • 射の結合は掛け算
  • 恒等射id*は1

関手としての ε:FinSkel→M では、FinSkelの対象はすべてダミー対象*に移されます。要するに、対象達は一点に潰されます。定義のためのΦの段階で Φ(f;g) = Φ(f)・Φ(g) などが成立するので、εも結合を保存して関手となります。

さらに、εは厳密モノイド関手になります。Mをモノイド圏とするにはモノイド積を入れる必要があります。可換モノイドから作られた圏では、モノイド積は結合と一致してしまいます。逆に、結合演算をモノイド積として使えば厳密モノイド圏になります。この事情については次の記事を参照してください。

以上のことからエディントンのイプシロンεは次のような厳密モノイド関手となります。

  • ε(f;g) = ε(f)・ε(g)
  • ε(f\oplusg) = ε(f)・ε(g)
  • ε(idn) = id* = 1 特に ε(id0) = 1