代入の圏Subst[Σ]上のラムダ計算

「置換の圏から代入の圏へ」で述べた圏Subst[Σ]上で、ラムダ計算をしてみます。ラムダ計算とはいっても、ラムダ風なだけで、構文は本来のラムダ計算からだいぶ離れます。

ランク付きアルファベットΣとしては、「置換の圏から代入の圏へ」の最後のほうで挙げた次の例を使います。

• Σ = ({c, f, g}, rank:{c, f, g}→N)
• rank(c) = 0, rank(f) = 1, rank(g) = 2

Subst[Σ] のなかで、c, f, g のプロファイルは以下のとおり。

1. c:0→1
2. f:1→1
3. g:2→1

c, f, gを含んだ組み合わせ（射）の一例、{x := f(y), y := g(y, c)} です。

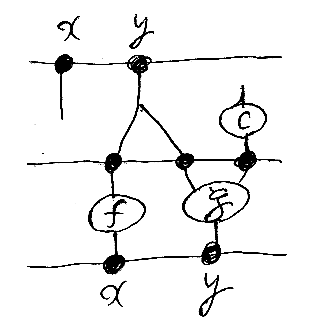
ここで出てきた変数 x, y, z などは便宜的なもので、Subst[Σ]に変数は含まれません。名前を持った変数は人間にとっては便利なものですが、ときに邪魔になることがあります。そこで、_1, _2, _3 のような番号による変数を使います。

xの代わりに_1、yの代わりに_2、zの代わりに_3を使うと、{x := f(y), y := g(y, c)} は {_1 := f(_2), _2 := g(_2, c)} と書けます。代入の表現 {_1 := F₁, _2 := F₂, ... } において、必ず左から順に番号を書くことに約束しておけば、{F₁, F₂, ... } と書いても同じです。これはもう単なるタプルなので、波括弧（ブレイス）から丸括弧に変えて (F₁, F₂, ... ) でもいいでしょう。

以上の約束に従うと、{x := f(y), y := g(y, c)} は (f(_2), g(_2, c)) となります。ラムダ抽象は、複数の変数を同時にラムダ束縛できる形だとして、λ(_1, _2).(f(_2), g(_2, c)) としましょう。もし、入力側に3番目の変数（絵では黒丸）があるとすれば、λ(_1, _2, _3).(f(_2), g(_2, c)) のようになります。

ラムダ抽象に使う変数リストを、常に (_1, _2, ..., _n) という形に限るなら、いちいち番号を並べる代わりに変数リストの長さだけを指定すれば十分です。そこで、λ(_1, _2, ..., _n) の代わりに λn と書くことにします。例えば、λ2.(f(_2), g(_2, c))、λ3.(f(_2), g(_2, c)) 。

「λ」の直後の数値（0以上の整数）と、ボディ部のタプルの長さから、射のプロファイルが分かります。例を挙げましょう。

1. λ2.(f(_2), g(_2, c)) :2→2
2. λ3.(f(_2), g(_2, c)) :3→2
3. λ0.(c, f(f(c))) :0→2
4. λ0.(c) :0→1
5. λ1.(c) :1→1
6. λ5.() :5→0

ボディ部が同じ形でもプロファイルが異なることがあります。λ0.(c)、λ1.(c)、λ2.(c) はみんな違う射です。デカルト圏における“第一射影”も、λ2.(_1)、λ3.(_1)、λ4.(_1) など色々あります。

λ3.(f(_2), g(_2, c)) のように、ラムダ変数（3つある）がボディ部に登場しないのは特に問題になりません。λ1.(f(_2), g(_2, c)) だと、変数_2が束縛されていません。_2は自由変数ということですが、用途によっては構文エラーにすることもあります。

ナカグロ記号「・」は、適用（application）ではなくて反図式順結合（anti-diagrammatic order composition）として使います。圏Subst[Σ]の結合そのものです。

---

これで、圏Subst[Σ]の射とその計算を完全に表すことができます。基本的な射をラムダ式で表してみましょう。

1. id₁ = I = λ1.(_1)
2. id₂ = II = λ2.(_1, _2)
3. σ = X = λ2.(_2, _1)
4. Δ = λ1.(_1, _1)
5. ! = λ1.()

{x := y, y := y, z := c} : 2→3 と {x := f(x), y := g(y, z)} : 3→2 は次のように書けます。

1. λ2.(_2, _2, c)
2. λ3.(f(_1), g(_2, _3))

結合の代入計算は次のようになります。

 λ3.(f(_1), g(_2, _3))・λ2.(_2, _2, c)
 // _1 := _2, _2 := _2, _3 := c
 = λ2.(f(_2), g(_2, c))

結合（・）の計算は、通常のベータ変換をタプル成分ごとに並列実行する操作になります。実際の計算を人がするときは、やはり変数に名前が付いていたほうがやり易いかもしれませんね。