モノイド閉圏：カリー化からニョロニョロまで - 檜山正幸のキマイラ飼育記 (はてなBlog)

昨日の記事「ラムダ計算の自然性とお絵描き」で、ラムダ計算を行える〈do lambda calculus〉環境としてのモノイド閉圏を紹介しました。モノイド閉圏はカリー化を持ちます。カリー化に関わる素材と法則があれば、そこから指数随伴系〈テンソル・ホム随伴系〉を構成できます。

この記事では、カリー化から出発して、随伴系 -- つまりニョロニョロ等式を満たす2-圏的構造を構成してみます。

内容：

随伴系の指標
指数随伴系
カリー化と反カリー化の対称性
二変数射と高階射
エバルとベータ変換等式
インスとイータ変換等式
随伴系の単位と余単位
ニョロニョロ等式
おわりに

随伴系の指標

随伴系〈adjunction | adjoint system〉の指標を書いてみます。指標については「構造とその素材の書き表し方」を参照してください。

signature Adjunction in CAT {
  sort A
  sort B
  operation F:A→B
  operation G:B→A
  two-operation η::A^⇒F*G:A→A
  two-operation ε::G*F⇒B^:B→B

  equation snake-1::: (η*F^);(F^*ε) = F^ :: F⇒F:A→B
  equation snake-2::: (G^*η);(ε*G^) = G^ :: G⇒G:B→A
}

まず、1行目の 'in CAT' で、この指標を考える場所は（小さいとは限らない）圏の圏 CAT だと分かります。CATは2-圏なので、対象（sort）、射（operation）以外に2-射（two-operation）があります。そして、随伴系の法則として3-射である等式（equation）があります。コロンの個数が射の次元に一致しています（sort＝0-射＝対象＝圏、operation＝1-射＝射＝関手、two-operation＝2-射＝自然変換、equation＝3-射＝自然変換の等式）。後置のカレット記号（'^'）は、“恒等”を作る演算子として使っています。A^ は圏Aの恒等関手、F^ は関手Fの恒等自然変換など。使っている二項演算子記号については、「関手と自然変換の計算に出てくる演算子記号とか // 今後使う予定の演算子記号」を参照してください。

この指標に出てきた2つの等式（snake-1とsnake-2）がニョロニョロ等式〈snake {equation | relation | identity | law}〉です。"snake"を「ニョロニョロ」と訳しはじめた経緯は次の記事を参照。

随伴系のインスタンスΣがあるとして、「構造とその素材の書き表し方」の標準的記法を使えば次のように書けます。

Σ = (Σ.A, Σ.B, Σ.F, Σ.G, Σ.η, Σ.ε)

「随伴に関する注意事項」に従って書けば：

Σ = (^Ση, ^Σε : ^ΣF -| ^ΣG, ^ΣF:^ΣA→^ΣB)

ここで、インスタンスΣを示す修飾子は左肩に付けています。右の上下添字は他の目的に使う可能性があるからです。後で、この書き方に近い記法を使います。

指数随伴系

モノイド閉圏Cの特徴は、対象 A∈|C| ごとに指数随伴系〈テンソル・ホム随伴系〉が存在することです。対象Aに対する随伴系を Σ[A] と書きましょう。Σ[A]の構成素に付ける添字はAだけにします。つまり、次のように書きます。

Σ[A] = (^Aη, ^Aε : ^AF -| ^AG, ^AF:^AA→^AB)

さらに次の約束をします。

^AF は、無名ラムダ変数やHaskell風セクション記法を使って直接書く。^AF = (- $\otimes$ A) = ( $\otimes$ A)
^AG も同様。^AG = [A, -]
Aが何であっても ^AA = ^AB = C であり、Cは了解されているので省略する。

結局、対象Aに対する指数随伴系Σ[A]は、

Σ[A] = (^Aη, ^Aε : ( $\otimes$ A) -| [A, -])

指数随伴系Σ[A]の存在を示すには、単位^Aηと余単位^Aεを定義して、それらがニョロニョロ等式を満たすことを示せばいいわけです。

が、いきなりニョロニョロ等式は難しいことがあるので、カリー化同型写像 Λ^X,A_Y:C(X $\otimes$ A, Y)→C(X, [A, Y]) からボトムアップで指数随伴系を組み上げることが多いでしょう。ここでもボトムアップ・アプローチを採用します。

カリー化と反カリー化の対称性

ラムダ計算では、カリー化〈ラムダ抽象〉、エバル〈evaluator〉*1、ベータ変換等式を主に扱います。反カリー化は積極的には扱いません。しかしここでは、カリー化と反カリー化を対等に対称的に扱います。カリー化Λの逆写像Λ^-1、つまり反カリー化をΓと書くことにします。

カリー化／反カリー化に関わる概念（まだ説明してない）を表にまとめておきます。説明は後述します。 $\newcommand{\id}{\mbox{id}}$

カリー化	反カリー化
写像 Λ	写像 Γ
エバル ev	インス ins
ベータ変換等式	イータ変換等式
ラムダベント $\overset{\lambda}{\cap}$	ガンマベント $\underset{\gamma}{\cup}$
余単位 ε	単位 η
テンソリング後結合	ホミング前結合
$\epsilon = \Gamma(\id_{[A, X]})$	$\eta = \Lambda(\id_{X \otimes A})$

Cの対象 X, A, Y の三つ組ごとに、カリー化／反カリー化のペアが与えられていて、次は成立していると仮定します。

Λ^X,A_Y : C(X $\otimes$ A, Y)→C(X, [A, Y])
Γ^X_A,Y : C(X, [A, Y])→C(X $\otimes$ A, Y)
Λ^X,A_Y;Γ^X_A,Y = id_{C(XA, Y)}
Γ^X_A,Y;Λ^X,A_Y = id_{C(X, [A, Y])}

$\require{AMScd} \begin{CD} {\mathcal C}(X \otimes A, Y) @>{\Lambda^{X, A}_Y}>> {\mathcal C}(X, [A, Y]) \\ @| @| \\ {\mathcal C}(X \otimes A, Y) @<{\Gamma^X_{A, Y}}<< {\mathcal C}(X, [A, Y]) \\ \end{CD}$

二変数射と高階射

昨日述べたように、カリー化の典型事例は「二変数関数から一変数高階関数」への変換、反カリー化の典型事例は「一変数高階関数から二変数関数」への変換です。

一般的な議論でも、この典型事例の“雰囲気”を醸し出すために、「二変数射」「高階射」という言葉を使いましょう*2。二変数射〈two-variable morphism | morphism of two variables〉とは、適当な対象 X, A, Y に対する X $\otimes$ A→Y というプロファイル（域と余域）を持つ射です。そして高階射〈higher-order morphism〉は、X→[A, Y] という、余域が指数〈内部ホム〉であるプロファイルを持つ射です。

Iをモノイド圏のモノイド単位対象とすれば、どんな射 f:X→Y でも、X $\otimes$ I→Y とみなすことができるので、二変数射だと言えます。また、X→[I, Y] という高階射とみなしてもかまいません。なので、二変数射／高階射という分類は絶対的な意味はないのですが、比喩としての心理的な効果はあり、説明には便利な言葉です。

ここから後の説明では、高階射（とみなしたい射）は、F, G などの大文字で表すことにします。例えば、カリー化Λの結果は高階射なので、G = Λ(f) のように書きます。ΓはΛの逆なので、Γ(G) = f ですね。

エバルとベータ変換等式

ラムダ計算を支配している法則は、ベータ変換等式だと言っていいでしょう。ベータ変換等式には次のモノが登場します。

カリー化 Λ = Λ^X,A_Y:C(X $\otimes$ A, Y)→C(X, [A, Y])
エバル ev = ^Aev_X : [A, X] $\otimes$ A→X in C

エバル（evaluatorの略称）と呼ばれる特別な射によって、カリー化の逆が作れることを主張するのがベータ変換等式です。公理的な定義では、ベータ変換等式を満たすような特別な射をエバルと呼び、その存在を公理的に要請します。よって、エバルとベータ変換等式は一緒に導入されます。

次の等式がベータ変換等式〈equation of beta reduction〉で、そこに登場する射 ^Aev_X がエバル〈eval | evaluator〉です。 $\newcommand{\For}{\mbox{For}\:\:}\newcommand{\cat}[1]{{\mathcal {#1}}}$

$\For f : X\otimes A \to Y \:\mbox{in}\: \cat{C},\\ (\Lambda^{X,A}_Y(f)\otimes \id_A);{^A ev_X} = f$

添字を省略して簡略に書けば：

(Λ(f) $\otimes$ A^);ev = f （A^ はAの恒等射）

ベータ変換等式を絵で描けば次のようになります。描画の約束は「ラムダ計算の自然性とお絵描き」を参照してください

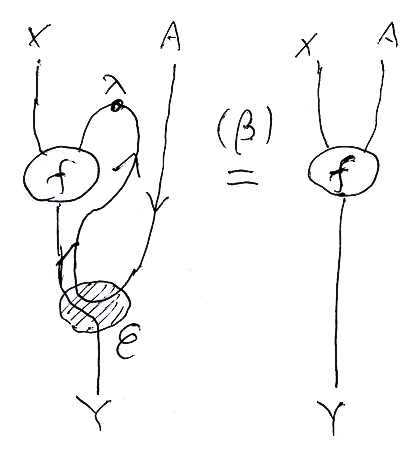
絵のなかで、小文字'λ'でマークされた部分をラムダベント〈lambda bent〉またはラムダカーブ〈lambda curve〉と呼びましょう。ワイヤー〈ストリング〉をラムダベントの形に曲げることがカリー化の実行になります。

'ε'でマークされたお団子〈ノード〉がエバルです。後で、ev = ε と別名を付けます。絵からの比喩的表現を使えば、ワイヤーAを思いっきり引っ張って真っすぐにすること〈ストレッチング〉がベータ変換です。引っ張ることにより、εが消滅し、ラムダベントは伸びます。

ベータ変換等式は、次のように解釈できます。

$G \mapsto (G \otimes \id_A);ev$ という対応は、カリー化Λの逆写像となる。

カリー化の逆写像は反カリー化Γなので、

$\Gamma(G) = (G \otimes \id_A);ev$

という、Γの具体的な表示が得られます。Γは、id_Aによる右テンソリング（モノイド積の意味の掛け算）して、evを後結合〈post-composition〉してます。

反カリー化Γは、テンソリングと後結合で作れる。

逆に反カリー化ありきなら、エバルは反カリー化から作れます。

$ev = \Gamma(\id_{[A, X]})$

エバルありきから反カリー化を作っても、反カリー化ありきからエバルを作ってもかまいません。いずれにしても、ベータ変換等式が構造と状況を統制しています。

インスとイータ変換等式

カリー化ではなく反カリー化をベースにして、前節と並行的に、インスとイータ変換等式を説明します。文面は、前節のコピーを修正したものです。

イータ変換等式には次のモノが登場します。

反カリー化 Γ = Γ^X_A,Y:C(X, [A, Y])→C(X $\otimes$ A, Y)
インス ins = ^Ains_X : X→[A, X $\otimes$ A] in C

インス（inserterの略称）と呼ばれる特別な射によって、反カリー化の逆が作れることを主張するのがイータ変換等式です。公理的な定義では、イータ変換等式を満たすような特別な射をインスと呼び、その存在を公理的に要請します。よって、インスとイータ変換等式は一緒に導入されます。

次の等式がイータ変換等式〈equation of eta reduction〉で、そこに登場する射 ^Ains_X がインス〈ins | inserter〉です。

$\For G : X \to [A, Y] \:\mbox{in}\: \cat{C},\\ {^A ins_X};[\id_A, \Gamma^{X}_{A,Y}(G)] = G$

添字を省略して簡略に書けば：

ins:[A^, Γ(G)] = G （A^ はAの恒等射）

イータ変換等式を絵で描けば次のようになります。

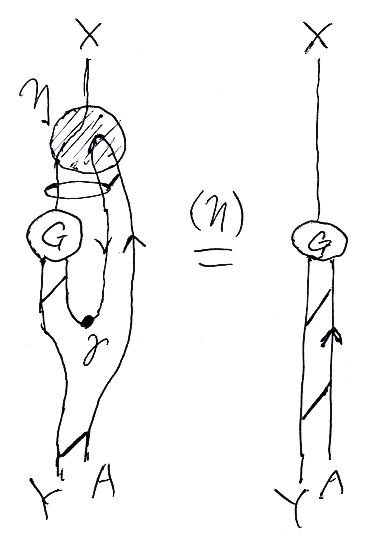
絵のなかで、小文字'γ'でマークされた部分をガンマベント〈gamma bent〉またはガンマカーブ〈lambda curve〉と呼びましょう。ワイヤー〈ストリング〉をガンマベントの形に曲げることが反カリー化の実行になります。

'η'でマークされたお団子〈ノード〉がインスです。後で、ins = η と別名を付けます。絵からの比喩的表現を使えば、ワイヤーAを思いっきり引っ張って真っすぐにすること〈ストレッチング〉がイータ変換です。引っ張ることにより、ηが消滅し、ガンマベントは伸びます。

イータ変換等式は、次のように解釈できます。

$f \mapsto ins;[\id_A, f]$ という対応は、反カリー化Γの逆写像となる。

反カリー化の逆写像はカリー化Λなので、

$\Lambda(f) = ins;[\id_A, f]$

という、Λの具体的な表示が得られます。Λは、id_Aによる左ホミング（内部ホムの意味の累乗）して、insを前結合〈pret-composition〉してます。

カリー化Λは、ホミングと前結合で作れる。

逆にカリー化ありきなら、インスはカリー化から作れます。

$ins = \Lambda(\id_{X \otimes A})$

インスありきからカリー化を作っても、カリー化ありきからインスを作ってもかまいません。いずれにしても、イータ変換等式が構造と状況を統制しています。

随伴系の単位と余単位

前々節と前節において、「エバルとベータ変換等式」と「インスとイータ変換等式」を並行的に扱いました。二種の概念群に対称性（あるいは双対性）があることが分かるでしょう。しかし、ラムダ計算では、「インスとイータ変換等式」はあまり注目しません。言及する場合でも、関数の外延性として紹介されます。そのときは、イータ変換の絵も次のように描かれます。

この暗い写真は2009年に僕が説明しているホワイトボードです。ちなみに、ベータ変換の説明は：

ちょうど10年前ですね（どうでもいけど）。

[補足]
カリー化＝ラムダ抽象はインスで表現可能で、反カリー化＝ラムダ反抽象はエバルで表現可能です。絵で考えれば、カリー化＝ラムダベンディング操作がインス＝ηノードのホミング前結合で表現され、反カリー化＝ガンマベンディング操作がエバル＝εノードのテンソリング後結合で表現されることになります。この状況は次の絵等式で覚えておくと便利です。

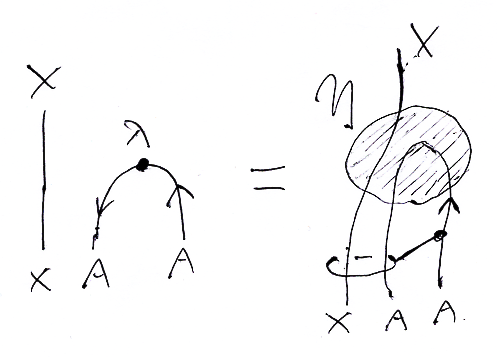
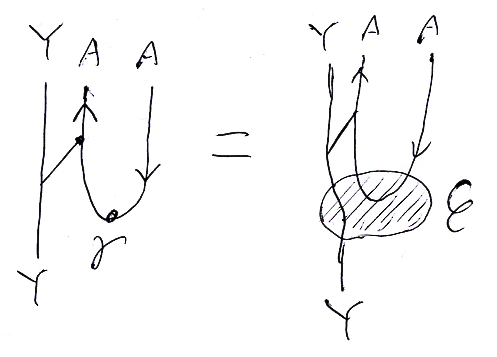
[/補足]

さて、今回エバルとインスを並行的／対称的に扱ったのは、随伴系にスムーズに結びつけるためです。次の事実があるのです。

エバルは指数随伴系の余単位である。
インスは指数随伴系の単位である。

随伴系における記法と合わせるために、次のように別名定義します。

^Aε = ^Aev
^Aη = ^Ains

^Aε, ^Aη は自然変換となり、次のプロファイルを持ちます。

^Aε:: [A, -] $\otimes$ A⇒C^:C→C
^Aη:: C^⇒[A, - $\otimes$ A]:C→C

対象Xでの成分を取れば：

^Aε_X: [A, X] $\otimes$ A→X in C
^Aη_X: X→[A, X $\otimes$ A] in C

^Aε, ^Aη が実際に自然変換になることは別途証明が必要ですが割愛します。

エバル（ev = ε）とインス（ins = η）、ベータ変換等式とイータ変換等式、それら全てを使うことによって指数随伴系が構成できます。

ニョロニョロ等式

カリー化 Λ(f) を f^∩ と書くと、絵と似ていて便利です。上付き'∩'がラムダベントを表します。 $\Lambda(f) = f^{\overset{\lambda}{\cap}}$ とかすると象形文字としての精度は上がりますが、そこまではしません。

ベータ変換等式は次のように書けます。

(f^∩ $\otimes$ A^);ε = f

前節の補足説明のように、ラムダベントをηノードのホミング前結合で置き換えていいので、

((η;[A^, f]) $\otimes$ A^);ε = f

結合とモノイド積に関する交替律〈interchange law〉を使うと：

((η $\otimes$ A^);([A^, f] $\otimes$ A^);ε = f

このなかの f:X $\otimes$ A→Y を特別に f = id_XA:X $\otimes$ A→X $\otimes$ A （Y = X $\otimes$ A）と置いても等式は成立します。実は、この等式が、指数随伴系のニョロニョロ等式になっています。そのことを絵で説明しましょう。

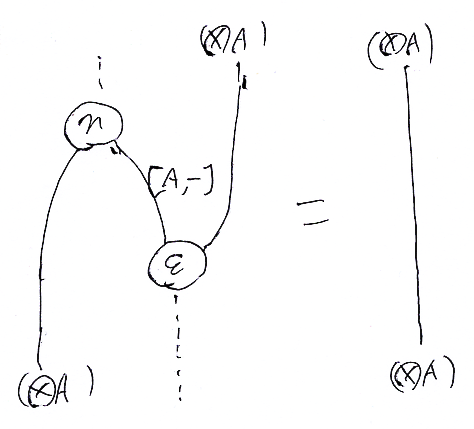
随伴系のニョロニョロ等式（の片一方）は (η*F^);(F^*ε) = F^ であり。指数随伴系では、F = ( $\otimes$ A), G = [A, -] でした。よって示すべき等式は、

η*( $\otimes$ A)^;( $\otimes$ A)^*ε = ( $\otimes$ A)^

です。絵に描けば：

対象Xでの成分を取ると：

X.(η*( $\otimes$ A)^;( $\otimes$ A)^*ε) = X.( $\otimes$ A)^

右辺の X.( $\otimes$ A)^ は、id_XA を意味します。

右辺に注目して絵に描いてみます。

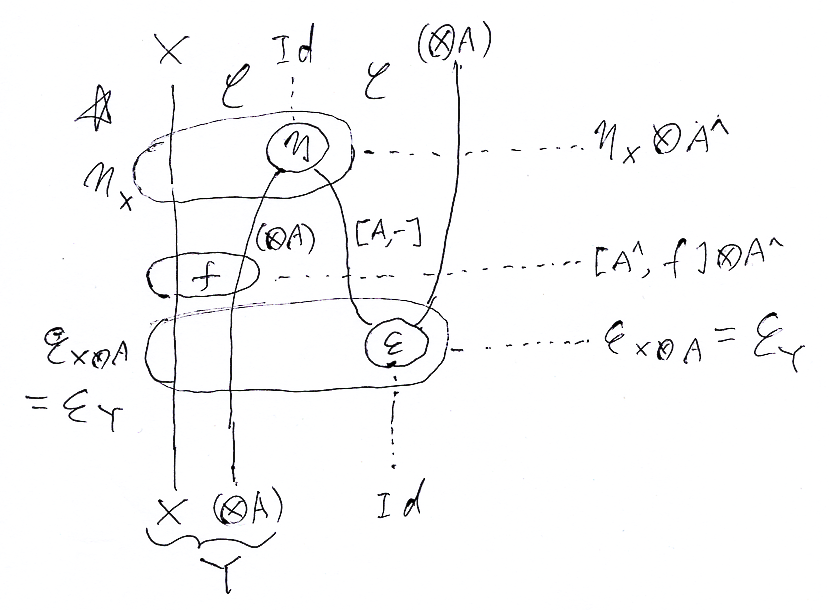
横に三段に分けて、各段のテキスト表現は：

η_X;A^
[A^, f] $\otimes$ A^
ε_XY = ε_Y

です。これを縦方向に結合すると、

η_X;A^ ; [A^, f] $\otimes$ A^ ; ε_Y
= (η;A^);([A^, f] $\otimes$ A^);ε

ところが、これは先の等式から f になります。f = id_XA だったので、ニョロニョロ等式が成立することが確認できました。

もうひとつのニョロニョロ等式に関しても同様にできます。

おわりに

この記事では、カリー化と反カリー化の対称性を強調しましたが、実際にはどちらか一方で十分です。例えば次の状況があったとします。

圏Cはモノイド圏であり、二項関手 [-, -]:C^op×C→C が備わっている。
圏Cの対象 X, A, Y ごとに写像 Λ^{X, A}_Y:C(X $\otimes$ A, [A, X]) が定義されている。
圏Cの対象 X, A ごとに特別な射 ^Aev_X:[A, X] $\otimes$ A→X が特定さている。
Λとevに関して、ベータ変換等式 (Λ(f) $\otimes$ A^);ev = f が成立している。

ベータ変換等式から、Λの可逆性が保証され、Λ^-1 := Γ, ins = Λ(id_XA) と定義すれば、反カリー化／インス／イータ変換等式の議論が展開できます。

ベータ変換等式／イータ変換等式があれば、それからニョロニョロ等式は導けるので、指数随伴系が構成可能です。別な言い方をすれば、カリー化／エバル／ベータ変換等式があれば、必然的に指数随伴系（の族）は存在します。

対象Aごとの指数随伴系達がテンデンバラバラではなくて、全体として体系的に連合していることを保証するには、カリー化の自然性を確認します。

以上のセッティングが揃えば、圏C上で型付きラムダ計算を行うことができます。

*1:"eval"だから「エヴァル」がいいという話があるかも知れませんが、長年「エバル」と言ってきたのでかえって違和感あります。そもそも僕は"b"と"v"をカタカナ表記で区別する必要性を感じません。「ベクトル」でいいし、「ベトナム」でいいよ。

*2:「使いましょう」と言いながら、この記事では使っていません。が、便利な言葉だとは思うので記述を残しておきます。