Globularはとっつきにくいソフトウェアなので、使い方を伝えるには、最初から順番に説明する必要があるでしょう。しかし、タクサンの画面キャプチャを撮ってマウス操作の説明を付けていく気力は湧きません(大変過ぎる!)。とりあえず、Globularのデモンストレーションとして、“それなりの内容の定理”を証明したサンプルをお見せします。誰でもアクセス可能なので体験して悟ってください(苦笑)。
「証明の過程を追体験する」の節だけは、頑張って手取り足取りな解説を書いたので、そのとおりに操作してみると雰囲気が伝わるでしょう。
このサンプルの内容はというと: 「絵算の威力をお見せしよう」において、ラルフ・ヒンズ(Ralf Hinze)の論文にある命題を2つ選んで絵に描きました。選んだ2つの命題は、論文の入り口にある補助的定理でしたが、今回はヒンズ論文の主要結果をまるまるGlobularで証明します。
テキストによる記述では、けっこうめんどくさい(と僕には思えた)定理が、絵では「そりゃ、そうだよな」と自然に納得できます。Globularの威力・効果は予想以上でした。
内容:
その他のサンプル:
例題:コモナドからモナドを作る
次の論文の主要結果を絵だけで証明します。
- Title: Theoretical Pearl / Monads from Comonads, Comonads from Monads / An Exercise in Program Transformation
- Author: Ralf Hinze
- URL: http://www.cs.ox.ac.uk/ralf.hinze/WG2.8/28/slides/Comonad.pdf
- Pages: 11p.
第4章の"Monads from comonads, comonads from monads"の冒頭に:
Assume that a left adjoint is at the same time a comonad. Then its right adjoint is a monad!
随伴対の左側が同時にコモナドでもあるとき、右側はモナドになる!
以上が定理の主張です。
もっとちゃんと述べましょう; Cを圏として、F, G:C→C は2つの自己関手とします。そして、FとGは随伴対を形成するとします。Cのホムセットを使って書くなら:
- C(F(X), Y)
C(X, G(Y))
ホムセットによる記述は絵算には向かないので、随伴の単位ηと余単位εを使ってニョロニョロ関係式を随伴の定義に採用します。([追記]ニョロニョロを随伴対の定義として採用すると、ホムセットの同型は定義から導出できることは、「Globularのサンプルを追加: 随伴対の二種類の定義」で示しています。逆の命題の絵証明は、ホムセットの絵による定義がよく分からなくて出来てません。[/追記])
- η::IdC⇒F*G:C→C
- ε::G*F⇒IdC:C→C
上記のテキスト記法は、絵算と相性が良いDOTN二号記法で、例えば F*G は、FとGのこの順での関手結合です。ニョロニョロ関係式は、後でGlobularの絵でお見せします。
さらに、随伴対の左相方Fはコモナドだとします。もちろん、正確には台関手F上にコモナドの構造が載っている、ということです。このコモナド構造を (F, δ, τ) とします。δはコモナドの余乗法(comultiplication)、τはコモナドの余単位です。随伴の余単位にεを使ってしまったので、τ〈タウ〉にしました。同じ「余単位」という言葉を使っていても、ここでは、随伴の余単位とコモナドの余単位は別物ですから注意。同様に、随伴の単位とモナドの単位も区別して下さい。
この状況で、随伴対の右相方G上にモナド構造 (G, μ, ι) を標準的(canonical, natural)な構成法で作れることがヒンズ論文の主要結果です。モナド乗法μとモナド単位ι(ηを使ってしまったのでι〈イオタ〉)は、与えられたη、ε、δ、τを組み合わせて作ります。証明が必要な肝心な所は、μの結合律とμとιに関する左右の単位律です。
この定理の具体的事例を挙げると、積コモナド(product comonad)から標準的にモナドを構成するとリーダーモナド(reader monad)となります。積コモナドとは、環境変数のような読み取り専用の大域変数を参照する計算を表現するコモナドです。実際これは、大域変数値の集合を直積で掛け算する型構成を台としたコモナドです。
今の文脈では余計な話ですが: 積コモナドとリーダーモナドは同値なことはこの定理から保証されますが、積コモナドのほうがずっと簡単でスッキリしています。それなのに、なんでシチめんどくさいリーダーモナドを皆さん使うのか僕はよく分かりません。
Globularにおける証明とは何か
冒頭で紹介したURL(以下に再掲)にアクセスすると、前節で説明した「随伴対の左側が同時にコモナドでもあるとき、右側はモナドになる!」定理の証明(を含んだワークスペース)が表示されます。Chrome以外のブラウザーでは描画がズレたりするようです。
まず注意しなくてはならないのは、様々ある絵を描く方向です。Globularの開発元組織である量子組(Quantum Group)の若頭はボブ・クックなので、絵の方向はクック流で「下から上↑」と「左から右→」です。
「絵算のススメ 2015 年末版」で紹介したダニエル・マースデン(Daniel Marsden)の絵も「下から上↑」「左から右→」で、レイアウト方式や色の使い方などもGlobularとよく似ているので、マースデンの解説は参考になるでしょう。
Globularにおける計算とか証明とは、画面中央の描画領域で作業した結果である絵を、左側のパネルにサムネイルとして登録していくことです。左側のパネルは正式には指標(signature)と呼びますが、お絵描きツールとしては図形パレットですね。パレットに入っている図形をセルと呼びます*1。セルは、制作した作品でもあり、次の作業の素材でもあります。
Globularは、通常の論理計算系や証明支援系が持っている構造や機能は何も持っていません。基本記号、項、論理式、シーケント、推論、証明といった各種構成要素や階層的な構造はないのです。公理、定義、定理の区別もこれといってありません。あるのは、各次元ごとのセルだけです。便宜上、セルを「対象、射、公理、定理、証明」などと呼び分けているだけです。これはホントに便宜上で、ゆるくて場合ごとに変わる対応です。
その事情を承知してもらった上で、今回のサンプルである"comonad to monad"のセルを全部列挙すると次のとおりです。
| 番号 | セル次元 | ラベル | 一言で説明 |
|---|---|---|---|
| 1 | 0 | C | ベースとなる圏C |
| 2 | 1 | F: C -> C | 随伴対の左相方 関手 F:C→C |
| 3 | 1 | G: C -> C | 随伴対の右相方 関手 G:C→C |
| 4 | 2 | eta:: Id_C => F*G | 随伴の単位 自然変換 η:: IdC⇒F*G |
| 5 | 2 | epsilon:: G*F => Id_C | 随伴の余単位 自然変換 ε:: G*F⇒IdC |
| 6 | 2 | comult:: F => F*F | コモナドの余乗法 自然変換 δ::F⇒F*F |
| 7 | 2 | counit:: F => Id_C | コモナドの余単位 自然変換 τ::F⇒IdC |
| 8 | 2 | mult:: G*G => G | モナドの乗法 自然変換 μ::G*G⇒G |
| 9 | 2 | unit:: Id_C => G | モナドの単位 自然変換 ι::IdC⇒G |
| 10 | 2 | 3-mult:: G*G*G => G | 3項の乗法 自然変換 3-μ::G*G*G⇒G |
| 11 | 3 | SNAKE-1 | ニョロニョロ関係式その1 |
| 12 | 3 | SNAKE-2 | ニョロニョロ関係式その2 |
| 13 | 3 | COASSOC | コモナドの余結合律 |
| 14 | 3 | L-COUNIT | コモナドの左余単位律 |
| 15 | 3 | R-COUNIT | コモナドの右余単位律 |
| 16 | 3 | mult Def | モナド乗法の定義 |
| 17 | 3 | unit Def | モナド単位の定義 |
| 18 | 3 | 3-mult Def | 3項モナド乗法の定義 |
| 19 | 3 | LEMMA-1 Theo | モナド結合律のための補題その1 |
| 20 | 3 | LEMMA-2 Theo | モナド結合律のための補題その2 |
| 21 | 3 | ASSOC Theo | モナドの結合律 定理 |
| 22 | 3 | L-UNIT Theo | モナドの左単位律 定理 |
| 23 | 3 | R-UNIT Theo | モナドの右単位律 定理 |
| 24 | 4 | LEMMA-1 Proof | 補題その1の証明 |
| 25 | 4 | LEMMA-2 Proof | 補題その2の証明 |
| 26 | 4 | ASSOC Proof | モナドの結合律の証明 |
| 27 | 4 | L-UNIT Proof | モナドの左単位律の証明 |
| 28 | 4 | R-UNIT Proof | モナドの右単位律の証明 |
セル達に対する解釈
Globularは、プレーン/ニュートラルな高次圏におけるセルの構成をサポートします。セルは0次元セルからはじめて次元の低いほうから順に構成していきます。どんな次元のセルでも作ろうと思えば作れますが、挙動が保証されているのは3次元までです。とはいえ、4次元・5次元あたりのセルは十分に使えますし、用途によっては必須です。
各次元のセルにどんな意味付けをするか、どう解釈するかはGlobularの問題ではなくて、我々使う側がその時々に決めることです。今回は次のような意味付けをしています。
- 0次元セル -- 圏
- 1次元セル -- 関手
- 2次元セル -- 自然変換
- 3次元セル -- 公理、定義、定理
- 4次元セル -- 定理の証明
例えば、コモナドの台である関手Fは1次元セルであり、コモナド余乗法と余単位は自然変換なので2次元セルです。そして、コモナドの結合律、左右の単位律は3次元セルです。
セルの描き方はビューのモード(レンダリング方式の選択)によって変わりますが、よく使うビューでは関手Fはピンクのストリング(紐)です。Fがコモナドであること(余結合律と左右の余単位律)は次のようなサムネイルで表示されます。
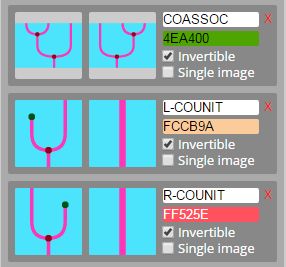
ピンクのストリングである関手Fとブルーのストリングである関手Gが随伴対であることは2つのニョロニョロ関係式で示せるので、次のようになります。

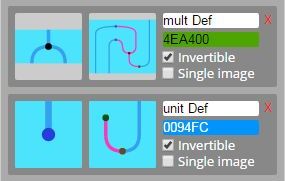
関手F上のコモナド構造 (F, comult, counit) をもとに、関手G上のモナド乗法multとモナド単位unitを定義します。その定義は以下のとおり
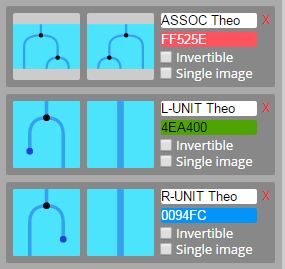
証明すべき定理のステートメントは、(G, mult, unit) における結合律と左右の単位律です。
[追記]
テキストによる記述では、けっこうめんどくさい(と僕には思えた)定理が、絵では「そりゃ、そうだよな」と自然に納得できます。
コモナド/モナドであることは実は使ってなくて、何であれ随伴・双対構造(ニョロニョロ構造)があれば、「左側にコモノイドがあれば、随伴で左右ひっくり返すと右側にモノイドができる」という一般的定理が言えます。コモノイドとモノイドに限らず、圏的等式的に定義される代数系なら、「ひっくり返すと双対的な代数系ができる」っていうほぼ自明な事実だったのです。複雑そうな状況を自明化してしまうのが絵算のパワーです。
[/追記]
証明の過程を追体験する
当初は「高次元の図形がなんで証明なんだよ?」という疑問が付きまとうと思います。その疑問に幾分か答えるために、モナド (G, mult, unit) の右単位律の“証明”を追いかけてみましょう。
まず、右側のClearボタンを押して、描画領域をクリアしておきます。画面左側のパレットの一番下に"R-UNIT Proof"(右単位律の証明)というセルがあります。サムネイルをクリックすると、中央の描画領域に当該セルが表示されます。
表示された図形は4次元図形なので、全体を一度に観察することはできません。右上のカウンターコントロールを Project[0], Slice[1][0] にセットしてください(下に画面ショット)。
この状態で表示されているのは、モナド乗法 "mult:: G*G => G" の右にモナド単位 "unit:: Id_C => G" をpre-composeで繋げたものです。絵の方向が下から上なことに注意して下さい。
Sliceの右のカウンターを 0, 1, 2, … と順に上げていきます。すると、合計10ステップの証明過程をパラパラ漫画として再現することが出来ます。
Globularの表示が不親切な(画面の情報が少ない)ので、証明の各ステップの根拠が分かりにくいのですが、この証明では次の根拠が使われています。
- unitの定義(unit Def)を展開
- multの定義(mult Def)を展開
- 交替律を適用
- 交替律を適用
- 交替律を適用
- 交替律を適用
- 交替律を適用
- ニョロニョロその2(SNAKE-2)を適用
- 左余単位律(L-COUNIT)を適用
- ニョロニョロその1(SNAKE-1)を適用
これらの変形により、初期状態の図形が関手G(の恒等)に等しいことが示せました。
証明の全体像は、Project[1], Slice[1] のビューで確認できます。

この図も下から上にと見ていきます。5つのドットの部分が、交替律以外を適用した証明ステップを表していて、マウスホバーでセル・ラベルがポップアップ表示されます。下から順に、
- unit Def
- mult Def
- SNAKE-2
- L-COUNIT
- SNAKE-1
となります。交替律の適用はストリング(紐)の交差(ブレイディング)として表示されます。
悟りなしの理解への道
冒頭で「体験して悟ってください」なんて言ってしまいましたが、「抽象的と具体的、自分の日本語が変で困った」で僕は、次のように記しています。
悟りを要求するとか具体性がないとは、「それは何なの? どういうことなの?」に対してキチンと答えられないような状況のことです。『燃えよドラゴン』のなかのブルース・リーは弟子に次のように言います。
- Don't think. FEEL. It's like a finger pointing at the moon.
考えようとする弟子に「考えるな」と、「感じるんだ」と。これはマジでカッコイイですね。カンフー(?)ではこれが教育法なのかも知れません。ですが、科学や技術に関わることで「考えるな、感じるんだ」が良い教育法だとは思えません。「月をさす指」を出されてもワケワカンナイだけです。
「感じるんだ」「月をさす指」みたいな話を僕は“具体性がない”と言います。仮に抽象度の高い概念をたくさん使っても、それによって「それは何なの? どういうことなの?」に対してキチンと答えているなら具体的です。抽象度の高い概念を知っているか/理解できるかはトレーニングの問題です。よく編成されたトレーニングコースに悟りは要らないはずです。
Globularを納得するのに、「月をさす指」も「悟り」も要らないのですが、高度にビジュアルで高度に対話的で、しかも高度に抽象的なソフトウェアについて、文字と静止画像の組み合わせで語るのはホントにシンドイです。「シンドイ」の代わりに「チャレンジング」と言うと、気分も変わるかも知れませんが。
*1:「セル」は本来は基本素材の意味ですが、素材を組み合わせて作った複合図形(複体)のこともセルと呼んでしまうことが多いです。