記法とは、読み書きの約束ごとです。視覚的媒体(紙、画面など)を通じたコミュニケーションには記法が必須です。広く合意・共有された記法が存在するので、我々は円滑なコミュニケーションを行えています。
一方で、特定の記法は人の発想や思考に強い制約を課します。記法が認知や理解の範囲を狭めて限定しているとも言えます。特にテキスト記法は、組版技術からの制約があって、柔軟性・自由度が乏しいために、我々の認知・理解の能力を押さえ込んでいるように思えます。伝統的・常識的記法のくびきから開放されれば、別な景色が見えるかも知れません。
記事タイトルの「記法バイアスと記法独立な把握」については、最後の節で説明します。実例に興味がない方は、最初の2節のあとに最後の節に飛んでもいいです。
内容:
語彙、文法、記法
マンガを読んだ経験がない人が初めてマンガを読もうとすると、読めないことがあるそうです。僕もある人に「どういう順番で読むの?」と聞かれたことがあります。コマを追えないのですね。
マンガは、アニメーションのように連続的な動きはしないので、コマとコマのあいだの時間経過・状態遷移を読者側で補完する必要もあります。なかには、読者に高度な補完能力を要求する作品もあるようです(僕よく知らないのだけど、士郎正宗作品はそうだと言われてます*1)。
マンガでも、文字による書き物と同様に、語彙や文法のような決まり/約束ごとがあり、それをマスターしないと読めないわけです。“コマ運び”が人間の直感ではなくて、社会(?)的規範であることは、例えば次の記事で分かるでしょう -- この記事はストリング図と絵算についてかなり示唆的です。
文字であれ絵であれ、語彙や文法のような決まり/約束ごとを、ここでは記法(notation)と呼ぶことにします。「記法」という言葉をとても広い意味 -- 「視覚的表現の規約と技法」として使います。小説には小説の記法があり、マンガにはマンガの記法があるのです。
特定の記法でないと表現できない事実や思いもあるかも知れません。しかし、同じ事実や思いを違う記法で表現することもあるでしょう。記法のあいだの翻訳はある程度は可能でしょう*2。慣れ親しんだ記法から別な記法に取り替えると、何か新しい知見や洞察が得られるかも知れません。
テキスト記法と絵図記法
Globularという証明支援系を紹介したことがあります。
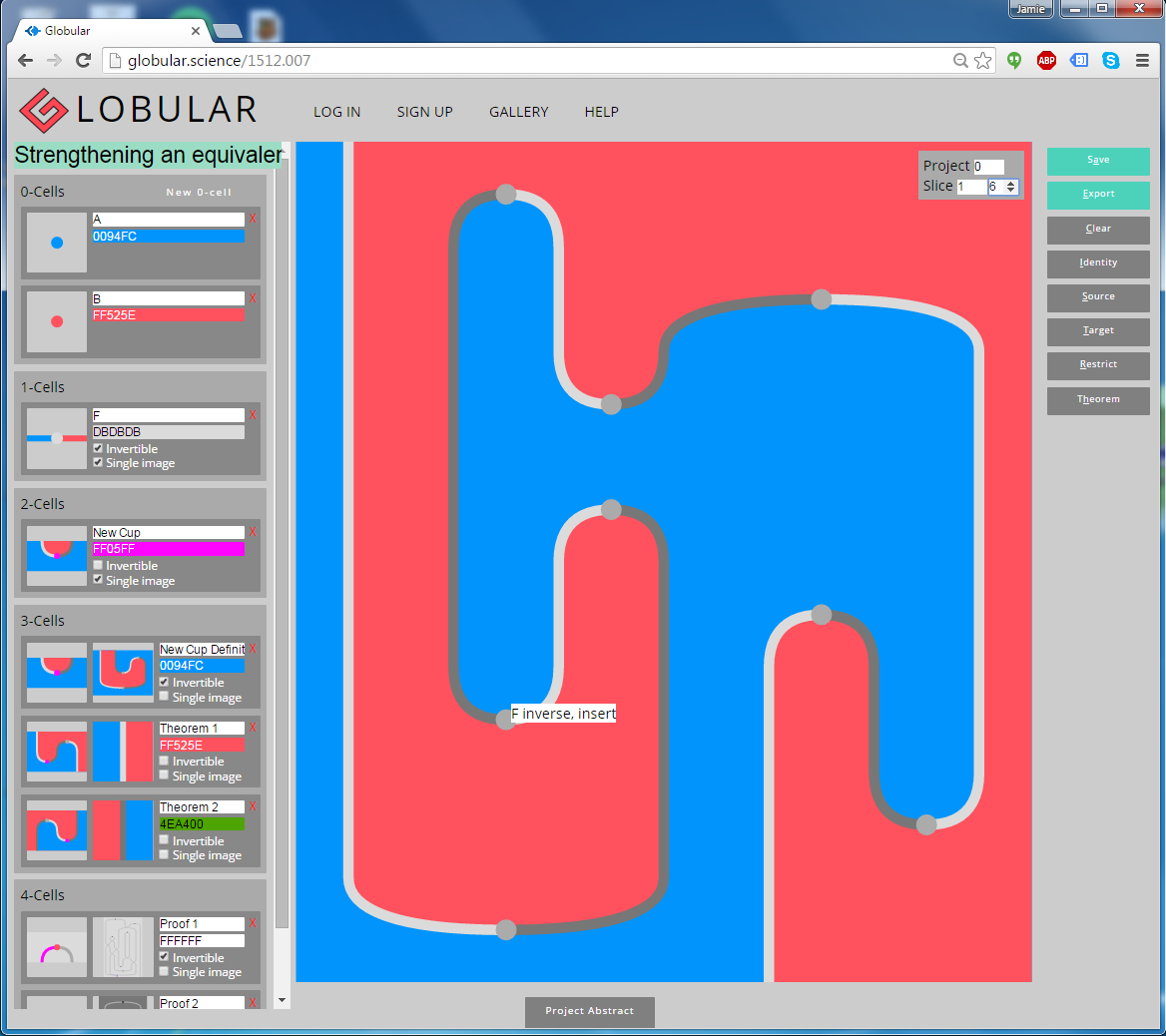
グネグネした絵をゴニョゴニョすると証明ができるソフトウェアです。絵を描く/絵をいじることが証明になることは、なかなか理解しがたいようです。では、Globularが採用している原理/背景理論が、通常のそれと全く別物かというと、そうではありません。“記法”が違うんです。
活字文化とマンガ文化にはギャップがあり、小説を読み慣れた人でもマンガのコマ運びに戸惑うように、通常のテキスト記法に慣れた人は、絵図による記述や証明行為に違和感をおぼえるのでしょう。
僕は、テキスト記法だけに頼るのは最早キビシイと思っています。「活字からマンガ/アニメーションへ」と同じ流れの変化が求められています。
一挙に絵図文化に移行する必要はありませんが、テキスト文化と絵図文化を架橋する試みは必要でしょう。
順序随伴と単位・余単位
テキスト文化と絵図文化のブリッジとして、「順序随伴性: ガロア接続の圏論」で取り上げた順序随伴を事例にします。
扱う話題は同じですが、上記の過去記事と少し記号を変えます。より圏論に寄せた記号法とします。
- プレ順序構造全体とその台集合(underlying set)を区別する。プレ順序構造全体をA、その台集合を|A|と書く。
- 単調写像を大文字のF, Gなどで表す。
- a≦b のような要素の順序関係に、φ, ψのようなギリシャ文字で名前を付けることがある。
- F≦G のような単調写像の順序関係に、α, βのようなギリシャ文字で名前を付けることがある。
3,4番目で言っていることは、φ:a≦b, α::F≦G のような記法(狭義)を採用する、ということです。φ:a≦b は、「a≦b であること」に'φ'という名前(ラベル)を付けた、あるいは「a≦b である証拠がφである」と解釈します。α::F≦G も同様です(コロンを2個付けているのは、要素の順序と写像の順序を区別するためです)。順序への名付けは、今回あまり使いませんが、圏とプレ順序集合の対応をとる際には重要です。
圏とプレ順序集合の対応は次のとおりです。
| 圏 | プレ順序集合 |
|---|---|
| 圏 C | プレ順序集合 A |
| 圏の対象類 |C| | プレ順序集合の台集合 |A| |
| 圏の対象 A | プレ順序集合の要素 a |
| 圏の射 f:A→B in C | 要素の順序関係 φ:a≦b in A |
| 関手 F:C→D | 単調写像 F:A→B |
| 自然変換 α::F⇒G:C→D | 単調写像の順序関係 α::F≦G:A→B |
さて、「順序随伴性: ガロア接続の圏論」で述べた次の定理を考えます。
- 単調写像FとGが随伴ペアである ⇔ FとGに関する単位・余単位不等式が成立する
ここで、「FとGが随伴ペアである」とは:
- a∈A, b∈B に対して、F(a) ≦ b ⇔ a ≦ G(b)
FとGに関する単位・余単位不等式とは次の2つの不等式です。(f, gをF, Gと大文字にしたのに合わせて、idをIdに変更しました。)
- IdA ≦ G・F
- F・G ≦ IdB
上記定理の半分だけを記述すると:
- FとGに関する単位・余単位不等式が成立するならば、FとGは随伴ペアである
この証明は次のように行いました。
仮定より F(a) ≦ b これとGの単調性から G(F(a)) ≦ G(b) ……(1) 単位不等式より a ≦ G(F(a)) ……(2) (1), (2), ≦の推移性より a ≦ G(b)
この定理(半分だけ)と証明を絵図記法へと翻訳してみます。
絵図を描けばこんな感じ
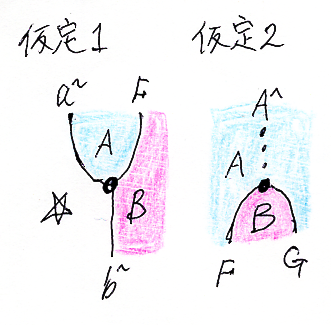
前節の定理では、次の2つの命題が仮定されます。
- 仮定1 F(a) ≦ b
- 仮定2 IdA ≦ G・F (単位不等式)
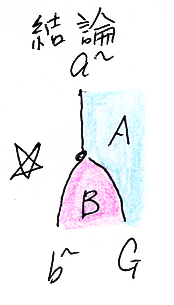
そして、結論は次の命題です。
- 結論 a ≦ G(b)
これら3つの命題に対応する絵図は次のようになります。
定理の証明は次の絵で示されます。
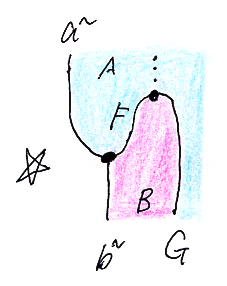
これを見て「はぁー、なにそれ?」と思った方もいるでしょうが、それは絵図記法に慣れてないからです。標準的テキスト記法の強烈なバイアスに支配されている、あるいは記法の獄舎に投獄されているからです。
標準テキスト記法を少しずつ変形しながら絵図記法に近付けていきましょう。
図式順記法
まずは、左から右に書ける図式順記法を導入します。圏論の用語を使いますが、実際に扱うのはプレ順序集合なので、話は簡単になります。心配いりません。
| 反図式順記法 | 図式順記法 | |
|---|---|---|
| 射の結合 | ψ |
φ;ψ |
| 関手の適用 | F(a) | a.F |
| 関手の結合 | G・F | F*G |
| 自然変換の適用 | αa | a.α |
| 関手と自然変換のヒゲ結合 | H・α, β・F | α*H, F*β |
| 自然変換の横結合 | β・α | α*β |
| 自然変換の縦結合 | β |
α;β |
圏論の用語とプレ順序集合に関する用語の対応は次のとおり。プレ順序集合に関する知識だけで十分です。
| 圏論 | プレ順序集合 |
|---|---|
| 射の結合 | 要素の順序関係の推移性 |
| 関手の適用 | 単調写像の適用 |
| 関手の結合 | 単調写像の結合(関数合成) |
| 自然変換の適用 | 単調写像の順序関係の要素ごとの具体化 |
| 関手と自然変換のヒゲ結合 | 単調写像の順序関係に単調写像を結合 |
| 自然変換の横結合 | 単調写像の順序関係の結合 |
| 自然変換の縦結合 | 単調写像の順序関係の推移性 |
図式順記法を導入すれば、絵図とテキストのあいだの向きの食い違いは解消できます。絵図を上から下/左から右に描けば、そのままの順序でテキストに写し取れます。
恒等単調写像 IdA:A→A をA^と書くことにします。これは“図式順”とは関係ありませんが、記法が単純化されます。a≦a に名前(ラベル)を付けるときも、a^を使って、a^:a≦a とします。
今問題にしている定理の仮定と結論を図式順記法で書けば:
- 仮定1 a.F ≦ b
- 仮定2 A^ ≦ F*G (単位不等式)
- 結論 a ≦ b.G
格上げと縦書き不等式
単一の要素からなるプレ順序集合を☆とします。要素は何でもいいですが、例えば |☆| = {0}、0^:0≦0 in ☆ と定義できます。プレ順序集合Aの要素a(a∈A)があるとき、a~:☆→A を次のように定義します。
- a~(0) = a
a~は自明ではありますが、単調写像に間違いはありません。(要素 a) |-> (単調写像 a~) と対応付ける操作を格上げ(promotion)と呼びます。格上げについては次の記事に色々書いてあります。
格上げを使うと、単調写像の要素への適用を、単調写像どおしの結合に置き換えることができます。
- (a.F)~ = a~*F (反図式順なら F(a)~ = F
a~)
要素aを生のまま使わずに、必ず格上げa~に置き換えれば、適用を使わずに結合だけで済みます。さらに、結合の演算子記号'*'(反図式順なら'・')を省略可能とすれば、次のようになります。
- (a.(F*G))~ = a~*(F*G) = a~ (F G) = (a~ F) G = a~ F G
要するに、演算子記号を使わずに、単に横に並べるだけで済みます。この記法で我々の定理の仮定と結論を書いてみると:
- 仮定1 a~ F ≦ b~
- 仮定2 A^ ≦ F G (単位不等式)
- 結論 a~ ≦ b~ G
実際には、モノグサ精神を発揮して、a~をa、A^もAと書いてしまうことが多いです。
- 仮定1 a F ≦ b
- 仮定2 A ≦ F G (単位不等式)
- 結論 a ≦ b G
次に不等式を縦書きしましょう。'≦'を縦方向にした文字(のグリフ)が欲しいのですが、見つかりませんでした。'△'で代用します。イコールを添えたいなら、'△‖'と'‖△' ですが、イコールは諦めて、'△'で縦方向の「ショウナリ・イコール」とします。すると:
仮定1 仮定2 結論 a~ F A^ a~ △ △ △ b~ F G b~ G
縦書き不等式からストリング図へ
a~, b~, A^, F, G はすべて単調写像なので、その域(始域)と余域(終域)であるプレ順序集合が定まっています。
- a~:☆→A
- b~:☆→B
- A^:A→A
- F:A→B
- G:B→A
域・余域の情報を、普通とは違う記法で書いてみます。
- (☆)a~(A)
- (☆)b~(B)
- (A)A^(A)
- (A)F(B)
- (B)G(A)
域・余域の情報を不等式に書き込むと:
仮定1 仮定2 結論
(☆)a~(A)F(B) (A)A^(A) (☆)a~(A)
△ △ △
(☆)b~(B) (A)F(B)G(A) (☆)b~(B)G(A)ウーン、鬱陶しいな。もう少しレイアウトを整理してスッキリさせましょう。
仮定1 仮定2 結論
a~(A)F A^ a~
☆ △ B A △ A ☆ △ A
b~ F(B)G b~(B)Gプレ順序集合☆, A, Bを色付き領域に、単調写像a~, b~, A^, F, Gをワイヤーに、単調写像のあいだの不等号△を黒丸ノードに置き換えれば、絵図(ストリング図)と同じになることがわかるでしょう。


不等式の証明
次に、仮定から結論に至る証明を見てみます。
まず、次の不等式を考えます。
- (1) A^ ≦ F G (仮定2 単位不等式)
- (2) a~ A^ ≦ a~ F G
(1)から(2)を出すリーズニング(証明を作り出す行為・過程)は次のように書けます。
- a~ ≦ a~, (1) A^ ≦ F G ⇒ (2) a~ A^ ≦ a~ F G
不等式を縦書きすれば:
a~ A^ a~ A^ △ (1)△ ⇒ (2)△ a~ F G a~ F G
今度は次の2つの不等式を考えます。(3)が抜けているのはミスではなくて、(3)は後で述べます。
- (4) a~ F ≦ b~ (仮定1)
- (5) a~ F G ≦ b~ G
(4)から(5)を出すリーズニングは:
- (4) a~ F ≦ b~, G ≦ G ⇒ (5) a~ F G ≦ b~ G
縦書きで:
a~ F G a~ F G
(4)△ △ ⇒ (5) △
b~ G b~ Gリーズニングの過程と結果をまとめてレイアウトすると、次のような図を描けるでしょう。
+---------------+ | a~ A^ | (2) △ (1)△ | | a~ F G | (3) | | a~ F G | (5) (4)△ △ | | b~ G | +---------------+
(3)の部分は、a~ (F G) = (a~ F) G という結合法則(上から下に読む!)を表しています。
さてところで、こんなアスキーアートを描くより、ストリング図のほうが楽だと思いませんか。対応するストリング図は次のとおりです。
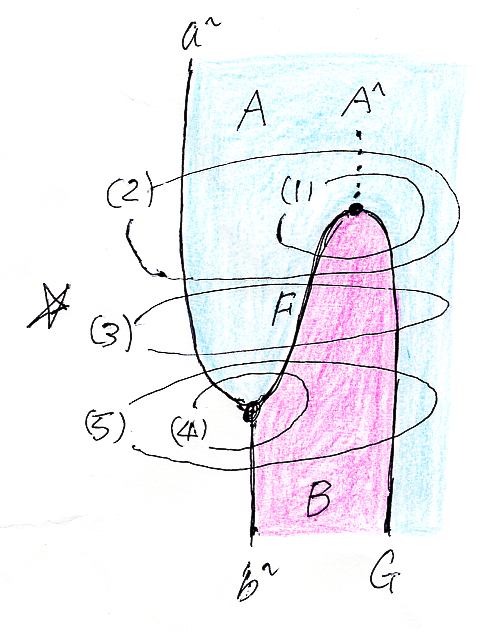
番号が付けられた部分に対応する不等式を繰り返し書き出すと:
- (1) A^ ≦ F G (仮定2 単位不等式)
- (2) a~ A^ ≦ a~ F G ((1)と a~ ≦ a~ から推論される)
- (3) a~ (F G) = (a~ F) G (結合法則)
- (4) a~ F ≦ b~ (仮定1)
- (5) a~ F G ≦ b~ G ((4)と G ≦ G から推論される)
証明の際の仮定(仮定1と仮定2)は、「使っていいよ」と与えられたピクチャーパズルのピースです。実際、証明ピクチャーの(4)と(1)の部分としてはめ込まれています。

それに対して結論は、出来上がりピクチャーの仕様です。仕様は、ピクチャーそのものではなくて、上部の入り口と下部の出口の状況と、領域分割のトポロジカルな特徴を規定するだけです。実際、証明ピクチャーを変形して単純化すれば結論になります。


マンガのコマを追う目線移動を習得しないとマンガが読めないように、ピクチャー(絵図)のなかにエンコードされた証明を読み解くには、絵の各部(ピース)を目線でトレースしながら解釈を積み上げる練習が必要です。
練習しても、それがプレ順序集合の不等式にしか使えないならモチベーションが湧きませんが、同様な手法・議論は極めて一般的な状況でも使えます。例えば、https://ncatlab.org/nlab/show/mate のProposition 1.1で述べられている2-圏の随伴に関するメイト定理は、今回と同じ絵で、解釈と証明ができます。
記法バイアスと記法独立な把握
我々が習った読み書き技法(リテラシー)は、文字を1次元に並べた離散的列を扱うだけです。その列は、多くの場合左から右への向きを持ちます。紙面・画面は有限なので折り返しはされますが、2次元構造を表現のために利用することはありません*3。
このため、たいていの人は“特定方向の1次元離散列”を超えた記法への適応性が乏しく、多次元や連続的図形を利用した視覚表現を受け入れて解釈することは困難です。向きだけ変えた縦書き数式にさえ戸惑います。
我々は、特定の記法に絡め取られて縛り付けられていると言えるでしょう。記法による拘束、固定化されてしまった認知方式を記法バイアス(notational bias)と呼びましょう*4。
記法バイアスのもとでは、本質的に同じ事実が異なる記法で書かれていると、その同一性を認識することができません。実際に、「記法が違うだけ」であることは多いので、記法バイアスが、ことの本質を捉える大きな障害になります。
例えば、今回話題にした順序に関する不等式 a≦b を、集合の包含順序では A⊆B と書きます。集合と述語は同一視可能ですが、述語(命題)の含意は P⊃Q と書きます。演繹定理から、P |- Q でも同じです。シーケント記法に直せば P→Q です。一方、自然演繹の証明図なら縦書きして、
P --- Q
横棒を縦矢印や縦不等号にしても同じです。下から上への方向もありです。
P ↓ Q or P △ Q or Q ↑ P
よりビジュアルにするならストリング図やペースティング図で描けばいいでしょう。文字の代わりにアイコンや色も使えます。
記法から完全に独立(independent)、中立(neutral)になるのは無理でしょうが、複数の記法を使ってものごとを眺めることはできます。特定記法にだけ縛り付けられない、より自由な了解のスタイルを記法独立な把握(notation free/independent comprehension/understanding)と呼びましょう。記法バイアスから開放されることです。
記法バイアスは、一種の習慣・文化・伝統であり、それ自体は悪いものではありません。ただ、単一の記法に固執するのは弊害がある; 控え目に言っても効率的ではありません。記法独立な把握のほうが効率的です。
とりあえずは、縦書き数式や鏡文字あたりから始めてはいかがでしょう(「双対や随伴に強くなるためのトレーニング」参照)。