簡単な例題のワークスペースを公開しました。
内容:
- 扱っているトピック
- 注意事項
- 指標(セル一覧)
- ワークスペースを作る手順
扱っているトピック
ワークスペースの内容は、「記法バイアスと記法独立な把握: 順序随伴を例として」そのままです。証明している定理は「順序随伴性: ガロア接続の圏論」に書いたものです。
次のセットアップ(状況設定)をします。
この状況のもとで、定理の仮定と結論は次のようになります。
- 仮定1: F(a) ≦ b
- 仮定2: idA ≦ G
F
- 結論: a ≦ G(b)
以上の状況と定理を、Globularのなかで再現し証明を与えたものが、当該ワークスペースです。
注意事項
僕が手書きで描いた絵をGlobularで再現するようにしました。しかし、手書きとGlobularでは方向の約束が違います。水平方向は左から右で同じですが、鉛直方向が違います。
- 檜山手描き: 上から下に向かう
- Globular: 下から上に向かう
檜山手描きの上下方向を逆にすると、Globularの絵になります。
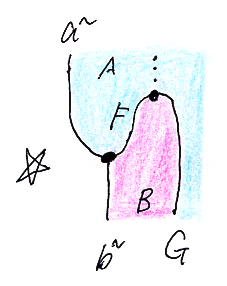

「記法バイアスと記法独立な把握: 順序随伴を例として」では、集合Aの要素 a∈A とその格上げ a~:☆→A を区別しました。Globularでは、集合の要素という概念はないので、aは自明なプレ順序集合IからAへの射としています。つまり、要素aと格上げa~の違いはないのです。なお、Globular内で非アスキー文字が使えないので、☆はIにしています。
指標(セル一覧)
指標(セルパレット)には合計11個のセルがあります。次元ごとの内訳は:
- 0次元セル 3個
- 1次元セル 4個
- 2次元セル 3個
- 3次元セル 1個
以下に、セル(指標の要素であるダイアグラム)を全部列挙します。セルの名前とプロファイルは、「名前:k ソース(域)→ターゲット(余域)」の書式です。ここで、kはセル次元。
| 番号 | 名前とプロファイル | 説明 |
|---|---|---|
| 1 | A:0 | プレ順序集合 |
| 2 | B:0 | プレ順序集合 |
| 3 | I:0 | 自明な(単元の)プレ順序集合 |
| 4 | a:1 I→A | Aの要素 |
| 5 | b:1 I→A | Bの要素 |
| 6 | F:1 A→B | 単調写像 |
| 7 | G:1 B→A | 単調写像 |
| 8 | Ass-1:2 (a F)→b | F(a) ≦ b という命題 |
| 9 | Ass-2:2 A^→(F G) | idA ≦ G |
| 10 | Concl:2 a→(b G) | a ≦ G(b) という命題 |
| 11 | Theorem:3 Concl→Proof | 定理の結論と証明 |
Ass-1:2(2-セルであるAss-1)が定理の仮定1、Ass-2:2が仮定2、Concl:2が結論です。定理の全体を表すTheorem:3は、結論であるConcl:2から証明を表す2次元ダイアグラムProofへの3次元セルです。Proofはセルパレットに登録されてない(したがって、セルではない)ですが、Theoremの一部なのでビューペインに表示できます。ワークスペースの初期状態では、2次元ダイアグラムProofがビューペインに表示されています。
ワークスペースを作る手順
公開されたGlobularワークスペースは、誰でも閲覧・調査できます。しかし、同じワークスペースをスクラッチから作る手順を伝える方法がありません。あるとすれば、動画(ビデオチュートリアル)でしょうが、手間がかかりすぎます。自然言語で長々・ダラダラと書くのは書き手/読み手、どちらにとっても苦痛です。
ここでは、簡単なスクリプト言語をでっち上げて、それを使って操作法を伝達することにします。
GUI/マウスで行う基本操作をオペレーションと呼び、名前を付けます。
| オペレーション名 | 説明 |
|---|---|
| New | パレット上部の"New 0-cell"ボタンを押すこと |
| Make | セルの名前(ラベル)と色を適切に設定すること |
| Select | マウスでセルを選択して、ビューペインに表示すること |
| Source | 画面右の"Source"ボタンを押すこと |
| Target | 画面右の"Target"ボタンを押すこと |
| Attach | マウスでセルを選択して、そのセルをダイアグラムに接着すること |
| Theorem | 画面右の"Theorem"ボタンを押すこと |
| SetView | ビューコントロールを設定すること |
Attachのとき、接着箇所の候補が出たときはそれを選びます。j番目の候補を選ぶことを Attach x (j) と書きます。実際の操作のときは、コマンドのショートカットキーを使うと速いです。
複数のオペレーションの順次実行の区切り記号にはセミコロンを使います。順次実行以外の制御構造はありません。
まず、セットアップ(状況設定)の手順を示します。
- New; Make A:0
- New; Make B:0
- New; Make I:0
- Select I; Source; Select A; Target; Make a:1 I->A
- Select I; Source; Select B; Target; Make b:1 I->B
- Select A; Source; Select B; Target; Make F:1 A->B
- Select B; Source; Select A; Target; Make G:1 A->B
これで使用する0-セルと1-セルが出来上がります。次に、定理の仮定となる2つの命題を2-セルとして構築します。
- Select a; Attach F; Source; Select b; Target; Make Ass-1:2 b->a F
- Select A; Identity; Source; Select F; Attach G (2); Targete; Make Ass-2:2 A^->F G
結論の2-セルを作る必要はありません(作ってもいいのですが、同じ内容のセルが重複してしまいます)。証明ダイアグラムの構成(リーズニング)は次のようにします。
- Select Ass-2; Attach a; Attach Ass-1; Theorem
- Make Concl:2 a->b G
- Make Theorem:3 Concl->Proof
証明ダイアグラムの部品(パーツ、ピース)としてAss-1とAss-2が使われていることが、これらが定理の仮定である意味です。Theoremコマンドは、2つのセルをパレット(指標)に追加します。
- 現在のダイアグラムと同じソース(域)とターゲット(余域)を持ち、唯一のノード(中心にある点)を持つダイアグラムを作り、セルとして登録する。
- 上記で作ったセルをソースとして、現在のダイアグラムをターゲットとして、唯一のノードを持つダイアグラムを作り、1次元高いセルとして登録する。
最初に作られたセルが定理の結論(あるいは定理のステートメント)を表します。二番目に作られた次元が高いセルは、定理の結論と証明(結論が成立する証拠)を結びつけるだけの役割です。
最後に、証明ダイアグラムをビューペインに表示しておきましょう。下のスクリプト内に出てくるTheoremは、Theoremコマンドではなくて、セルの名前としてのTheoremです。ちょっとややこしかった。
- Select Theorem; SetView(Project=0, Slice=1)