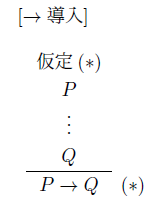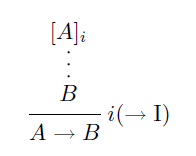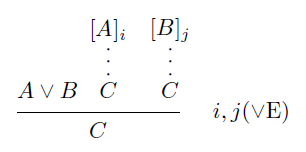自然演繹は、その名の通りに「自然で分かりやすい」と言われたりします。僕は、そうは思いません。むしろ「不自然で分かりにくい」と感じます。導入規則と除去規則のあいだに綺麗な対称性がある、と言う人がいます。僕にはどこが綺麗か分かりません。無理クリに対称に見せてるだけで、むしろ歪んでいて汚ないじゃないか、と思います。
自然かどうか、綺麗かどうかは主観の問題ですから、議論しても不毛です。しかし、代替の定式化を示して、それを自然演繹と比較することにより、自然演繹を相対化することは出来ます。やってみます。
この記事の内容は、ここ10年くらい思っていたことです。口頭でしゃべったことはありますが(最後の節を参照)、まとまった記述はなかったので、割と丁寧に書きました。その結果、けっこう長大な記事となりました。
論理や圏論を学ぶには、まっとうな教科書を手元に置くのがよいでしょう。その教科書が主治医とするなら、僕の記事はちょっと変わったセカンドオピニオン程度の参考になれば幸いです。
内容:
- 自然演繹はどこがダメなのか
- 自然演繹の推論図の例
- この記事の方針と記号の約束
- 自然演繹の推論図一式
- 暗黙の前提もちゃんと描くと
- 自然演繹からシーケント計算へ
- 証明オブジェクトとリーズニング
- セマンティック駆動な圏的意味論
- 圏論的に自然な演繹とは
- 存在が保証された射
- 圏論的に自然なリーズニングの例 その1
- 表現は色々あっても実体は同じ
- 圏論的に自然なリーズニングの例 その2
- 僕が思っていたこと/思っていること
関連する記事:
自然演繹はどこがダメなのか
僕が自然演繹はダメだと思う理由は次の2点です。
- 自然演繹で通常使われる推論図/証明図の図示法は、できが悪く分かりにくい。
- セマンティクス(意味論)との対応を取りにくい。
図示法の問題点をもっと詳しく言うと:
- 本来、時間に沿って変化するアニメーションであるものを、無理に1枚の静止画で描くので、意味不明となる。
- 図に描かれてない、暗黙の前提(不可視な了解事項)が多すぎる。
- 証明を進めるために、証明図の局所的な追加変更だけでは済まず、全面描き換えが発生する。
例えば、含意導入規則の推論図は次のように描かれます。
[A] ・ ・ ・ ----- A⊃B
この図を見て含意導入を理解できるのは既に知っている人で、はじめての人がこの絵をスンナリ理解できるとは考えにくいです。
含意導入規則は、証明図の時間的変化のことですから、変化のbeforeとafterがあります。ですから、少なくとも2枚の絵により表現すべきことです。
before A ・ ・ ・ ----- B after [A] ・ ・ ・ ----- B ----- A⊃B
もちろん、縦に並んだ点々や、afterのAをブラケットで囲んでいることなどは別途説明が必要です。
自然演繹の推論図の例
自然演繹の図示法は「できが悪く分かりにくい」と言ったのですが、とりあえずは現状の図示法がどんな感じかを紹介します。インターネット上で見つけた自然演繹に関する解説から、含意の導入と選言の除去に関する規則の図(推論図)を見てみましょう。
http://logicmanual.philosophy.ox.ac.uk/jsslides/ll6p.pdf より
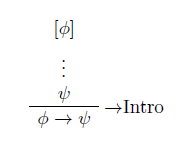
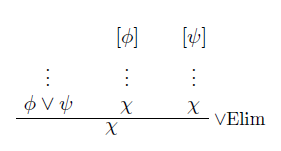
細部では差がありますが、図示法の基本は共通していることが分かるでしょう。
念のためにお断りしておきますが、僕は自然演繹の伝統的な図示法そのものが問題を抱えていると思っているのであって、上記に挙げた解説やまとめは優れたものです。誰がやったところで、伝統的な図示法を分かりやすく解説することには限界があります。だって、本質的に分かりにくいんだもの。
この記事の方針と記号の約束
ここでは、自然演繹とシーケント計算は事実上同じだとみなします。自然演繹とシーケント計算は表現方法が違うだけで、同じモデルを持つということです。
ではモデルとは何でしょうか。ここでは、直和を持つデカルト閉圏を論理システムのモデルとします。むしろ、デカルト閉圏が先にあり、それの記号的表現として論理システムを考えます。意味論(セマンティクス)を先に考えて、構文論を後から付けるスタイルで、僕が「セマンティック駆動」と呼んだ*1やり方です。
デカルト閉圏から出発するセマンティック駆動な計算については既に述べています。
必要があれば上記の記事群を参照してもらうことにして、この記事で使う記号を約束しておきます。
論理結合子としては、∧、∨、⊃ を使います。含意は → ではなくて ⊃ を使います。論理定数は⊥(矛盾、偽)とI(真)です。直和を持つデカルト閉圏との関係は次のようです。
| 論理 | 圏論 | ひとこと |
|---|---|---|
| A∧B | A×B | 連言、直積 |
| A∨B | A + B | 選言、直和 |
| A⊃B | BA | 含意、指数 |
| ⊥ | 0 | 偽、始対象 |
| I | 1 | 真、終対象 |
「圏論からシーケント計算へ」と同じ記号にしています。否定(¬)はありませんが、必要なら、¬A は A⊃⊥ の略記だとします。
矢印 → は、シーケントの左右区切りに使います(含意ではありません!)。自然演繹の証明図は、シーケントと同じ意味だとします。つまり:
A ・ ・ ・ --- B
このような証明図があるとき、それを横方向にして A → B と書こう、ということです。
この対応関係をよりハッキリさせるために、証明図の一部省略を表す点々を縦向き矢印で書くことにします。A, B → C というシーケントに対応する自然演繹証明図は次のように書きます(描きます)。
A B
-----
↓
B
縦向き矢印↓の部分には、なにやらあるかも知れないが、その詳細は問題にしない、ということです。
自然演繹の推論図一式
自然演繹の推論図/証明図のメリットは、テキストでも描けることです。以下に、伝統的な自然演繹の8つの推論図を列挙します。
A B
-------[∧導入]
A∧B
A∧B
-----[∧除去1]
A
A∧B
-----[∧除去2]
B
A
-----[∨導入1]
A∨B
B
-----[∨導入2]
A∨B
A B
--- ---
↓ ↓
A∨B Y Y
-------------[∨除去]
Y
[A]
---
↓
B
-----[⊃導入]
A⊃B
A⊃B A
--------[⊃除去]
B
これらの推論図が、セマンティックに(意味論から)導けることを示し、セマンティック駆動なシーケント計算との対応を付けることがこの記事の目的です。
暗黙の前提もちゃんと描くと
再度、http://logicmanual.philosophy.ox.ac.uk/jsslides/ll6p.pdf の図を引用します。
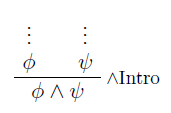
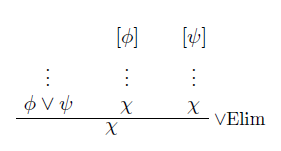
他の資料の図では付いてない縦の点々が付いてます。この点々をちゃんと描くことにします。さらに、点々の上側にあるはずの仮定を描きます。点々を下向き矢印で代用すると次のようになります。
Γ Δ --- --- ↓ ↓ A B -------[∧導入] A∧B
Γ A B
--- --- ---
↓ ↓ ↓
A∨B Y Y
-------------[∨除去]
Y
ここで、ΓとΔは、いくつか(0個かもしれない)の論理式の並びを1文字で表現したものです。
「自然演繹はどこがダメなのか」において、「本来、時間に沿って変化するアニメーションであるものを、無理に1枚の静止画で描くので、意味不明となる」と指摘しました。であるならば、ひとつの推論規則を、beforeとafterに分けて描くことにすればよいでしょう。(次の図で、レイアウトのバランスを取るために、縦向き矢印を余分に挿入しています。)
[∧導入 before] Γ Δ --- --- ↓ ↓ A B [∧導入 after] Γ Δ --- --- ↓ ↓ A B ------- ↓ A∧B
[∨除去 before] Γ A B --- --- --- ↓ ↓ ↓ A∨B Y Y [∨除去 after] Γ --- ↓ A∨B ---- ↓ Y
after側の詳細を気にしないなら、中間部分を矢印に押し込めて次のようになります。
[∧導入 before] Γ Δ --- --- ↓ ↓ A B [∧導入 after] Γ Δ -------- ↓ A∧B
[∨除去 before] Γ A B --- --- --- ↓ ↓ ↓ A∨B Y Y [∨除去 after] Γ --- ↓ Y
縦方向の書き方から横方向の書き方にして、before/afterを上下の段で表すなら:
before Γ→ A Δ → B ========================[∧導入] after Γ,Δ → A∧B
before Γ → A∨B A → Y B → Y ====================================[∨除去] after Γ → Y
自然演繹の推論図/証明図と区別するために、横線を二重(イコールの並び)にしました。
自然演繹からシーケント計算へ
もうお分かりと思いますが、自然演繹の推論図のbefore/afterを明示的にちゃんと書いて、よりコンパクトにすると、結局はシーケント計算になります。先に挙げた自然演繹の推論図に対応するシーケント計算の8つの推論図は次のようになります。上段がbefore、下段がafterです。
Γ→ A Δ → B
=================[∧導入]
Γ,Δ → A∧B
Γ → A∧B
===========[∧除去1]
Γ→ A
Γ → A∧B
===========[∧除去2]
Γ→ A
Γ → A
===========[∨導入1]
Γ→ A∨B
Γ → B
===========[∨導入2]
Γ→ A∨B
Γ → A∨B A → Y B → Y
=============================[∨除去]
Γ → Y
Γ,A → B
===========[⊃導入]
Γ → A⊃B
Γ → A⊃B Δ → A
====================[⊃除去]
Γ,Δ → B
シーケントに書き換えることにより、スペースを必要とする縦方向の図が横方向1行で書けます。また、before/afterを上段/下段に分離するので「無理に1枚の静止画で描くので、意味不明」な問題は解決します。暗黙の前提をΓなどで明示しているので「図に描かれてない、暗黙の前提(不可視な了解事項)が多すぎる」も解決します。
シーケント計算の証明図は、自然演繹の証明図の描き換えを上段と下段として記録するので、シーケント計算の証明図の全面描き変えは発生しません。ツリー状の図形が上から下、または下から上に成長していくだけです。これで、自然演繹の証明図の三番目の問題「証明図の局所的な追加変更だけでは済まず、全面描き換えが発生する」が解決します。もっとも、自然演繹レベルの全面書き換えの前後を簡略化して記録しているだけなので、描画の手間はたいして減りません。
こう言うと、シーケント計算はいいことずくめのようですが、欠点もあります。自然演繹の証明は、それを描く中間段階を見なくても、最後に得られた証明図だけ見れば、証明の正しさを判定できます。一方、シーケント計算では、最後に得られたシーケント(最下段のシーケント)を見ても、証明全体の正しさを検証できません。これは、シーケント計算の証明図の上段から下段に移るとき、情報を落としているからです(自然演繹では情報が累積されます)。実用上は、証明の正しさの証拠となる単一のデータがあったほうが便利です。
証明オブジェクトとリーズニング
前節の最後で言った「証明の正しさの証拠となる単一のデータ」を証明オブジェクト(proof object)と呼びます。証明オブジェクトとして使われるデータの種類は次のモノがあります。
- ラムダ計算の項
- 自然演繹の証明図
- ストリング図
意味論にデカルト閉圏を使うなら、この3つは実際は同じものです。いずれも、デカルト閉圏の射を表現する形式なのです。「ラムダ計算の項」と「自然演繹の証明図」が同じであることを具体的に示せば、それがカリー/ハワード対応になります。
「証明」という言葉が、証明オブジェクトというデータを表すこともありますが、証明オブジェクトを作り出す行為を「証明」と呼ぶこともあります。この2種の「証明」はシッカリ区別すべきです。「証明オブジェクト」と「証明行為」とすれば区別できますが、もっと明確に区別するために、証明行為をリーズニング(reasoning)と呼ぶことにします。
すると、次のことが言えます。
- 自然演繹では、証明オブジェクトを証明図として図示する。リーズニングを図示する方法はなくて、リーズニングの扱いは曖昧なままである。
- シーケント計算では、リーズニングを証明図として図示する。証明オブジェクトは定義されてなくて、証明オブジェクトは無視されたままである。
伝統的論理のなかでは、証明オブジェクトとリーズニングの両方をちゃんと記述する方法がないのですよね。ちゃんと書く(描く)と、情報が多いので冗長/煩雑/めんどくさい、って事情はあります。
型理論では、型判断(typing judgement)をシーケントとして、ラムダ項の型付けを証明図風に描きますが、これは証明オブジェクト(ラムダ項)とリーズニング(型付けの行為)の両方を記述していると言えます。
セマンティック駆動な圏的意味論
セマンティック駆動な立場では、デカルト閉圏(やその拡張)が先にあり、その圏を記述・計算するための記号的体系を後から準備します。Cがモデル(意味領域)となる圏だとすると、Cの対象そのものを原子論理式(基本命題)として採用します。なお、論理式と命題はここでは同義語とします。
論理記号 ∧, ∨, ⊃, ⊥, I はそれぞれ、圏Cの 直積、直和、指数、始対象、終対象 と解釈します。“基本命題=Cの特定の対象”から論理記号を使って組み立てられた論理式は、Cの対象と同一視します。
命題(論理式)をカンマで区切った列 A1, ..., An は、A1∧...∧An と解釈します。そして、シーケント A1, ..., An → B の意味は、Cのとある射 f:A1∧...∧An→B in C のことです。「セマンティック駆動な圏的ラムダ計算とシーケント」の「型シーケント」も参照してください。
もっと正確な議論をしたいなら、複圏(オペラッド)、多圏を導入する必要がありますが、複圏/多圏の話題は先延ばしになっています。
命題(Cの対象)をカンマで区切った列をΓとして、シーケントの一般的な形は Γ → B となります。カンマをCの直積だと解釈して、シーケントはCの射を表すことになります。Γが空列のときは、I→B in C (Iは終対象)という射とします。
シーケントを圏の射とみなす話は、次の記事でもう少し詳しく書いています。
圏論的に自然な演繹とは
今までに述べたことをまとめると:
- 証明オブジェクトに焦点を合わせ、リーズニングについては曖昧イイカゲンにしてしまった定式化が自然演繹。
- リーズニングに焦点を合わせ、証明オブジェクトは無視してしまった定式化がシーケント計算。
- 「どこに注目するか?」と表現方法は異なるが、自然演繹もシーケント計算もやっていることは同じ。
「演繹系とお絵描き圏論」で述べたように、「TEH・自然演繹」や「THE・シーケント計算」があるわけではないので、定式化を微妙に変えるだけでいくらでも変種(バリアント)を作れます。実際に無闇と変種があるので、論理のお勉強が博物学・分類学になる傾向があるわけです(このことは「論理とはなにか?」でも指摘しました)。そして、「論理におけるさまざまな「矢印」達」で述べたように、用語と記号もグジャグジャです。
型理論では、ラムダ式(ラムダ計算の項)を証明オブジェクトとして、シーケント計算風の型付け(typing)の導出ツリー図でリーズニングを表しています。証明オブジェクトとしてラムダ式に拘る必要もないので、圏論で通常使われる記法による式(expression)を証明オブジェクトにしてもいいでしょう。
圏論で通常使われる記法とは:
- 射 f:A→B と g:B→C の結合(composion)は f;g:A→C と書く。
- 射 f:A→B と g:C→D の直積(デカルト積)は f∧g:A∧C→B∧D と書く。
- 射 f:A→Y と g:B→Y のデカルト余ペアリングは [f, g]:A∨B→Y と書く。
記号を増やしたくないので、「圏の直積/直和/指数」も論理記号「∧/∨/⊃」で表すことにします。三番目のデカルト余ペアリングは、デカルトペアリング <f, g>:X→A∧B の双対で、次の等式が成立します。
- <f, g> = ΔX;(f∧g) (ΔXは対角)
- [f, g] = (f∨g);∇Y (∇Yは余対角)
シーケント A1,...,An → B では、左側がカンマで句切られた列なので、結合が少し変形されて次のようになります。
- f:A1∧...∧An→B と g:B∧C1∧...∧Cm→D の結合を f;Bg:A1∧...∧An∧C1∧...∧Cm→D とする。
f;Bg という記法の意味は、(f∧idC1∧...∧Cm);g です。絵で描けば次のよう。
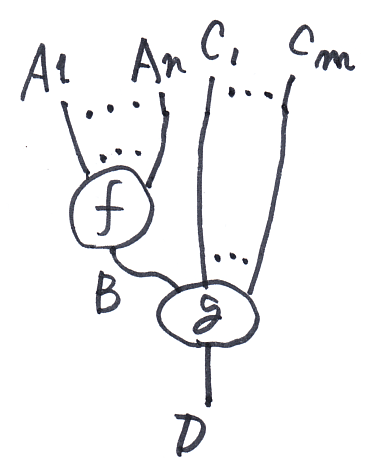
Cはデカルト閉圏なので、カリー同型があります。
- C(X∧A, B)
C(X, A⊃B)
この同型の左から右に向かうカリー化写像を ΛX A B (大文字ラムダ)とします。下付き添字内の区切りにカンマではなくて空白を使っているのは、カンマが直積の意味で使われているからです -- A,B = A∧B。
結合、直積、余ペアリング、カリー化という圏論的オペレーションをリーズニングの基本ステップとみなすと、次のような4つの基本リーズニング図が得られます。
f:Γ → A g:A,Δ → B =======================[comp 射の結合] f;Ag:Γ,Δ → B f:Γ → A g:Δ → B =====================[prod 射の直積] f∧g:Γ,Δ → A∧B f:A → Y g:B → Y ===================[copair 射の余ペアリング] [f, g]:A∨B → Y f:Γ,A → B ===================[curry カリー化] ΛΓ A B(f):Γ→A⊃B
自然さは主観的です。既知の事項や過去の経験とのギャップが少ないと「自然だ」と感じるのでしょう。「既知の事項や過去の経験」は人ごとに違うので、自然さも人ごとに違うことになります。デカルト閉圏の知識と経験があるなら、上記の4つのオペレーションを基本とする演繹系は自然なものとなるでしょう。
僕が言いたいことは、伝統的な自然演繹の“自然さ”に強い根拠はない、ということです。対称だ、綺麗だ、というのも、気分と趣味の問題に過ぎません。例えば、モデルとなるデカルト閉圏ありきの立場なら、伝統的な自然演繹は使い勝手が悪く、「自然でも対称でも綺麗でもない」と感じることでしょう。この感覚が、この記事のタイトルの由来です。
存在が保証された射
Cが直和を持つデカルト閉圏ならば、存在が保証された対象や射があります。例えば、終対象かつ直積の単位である1、始対象かつ直和の単位である0は存在が保証された対象です。この2つの対象は、本記事内では論理定数I、⊥で表現されています。
どんな圏であれ、対象Aに対する恒等射 idA:A→A の存在は保証されます。終対象、始対象があるので、!A:A→I、θA:⊥→A も存在が保証されています。このような、在ると分かっている射を列挙しましょう。
| 記号 | 呼び名 | プロファイル | ひとこと |
|---|---|---|---|
| idA | id | A→A | 恒等射 |
| !A | term | A→I | 終対象への唯一射 |
| θA | init | ⊥→A | 始対象からの唯一射 |
| π1A B | proj1 | A∧B→A | 直積の第1射影 |
| π2A B | proj2 | A∧B→B | 直積の第2射影 |
| ι1A B | inj1 | A→A∨B | 直和の第1入射 |
| ι2A B | inj2 | B→A∨B | 直和の第2入射 |
| λA | lunit | I∧A→A | 左単位律子 |
| ρA | runit | A∧I→A | 右単位律子 |
| αA B C | assoc | (A∧B)∧C→A∧(B∧C) | 結合律子 |
| σA B | symm | A∧B→B∧A | 対称 |
| ΔA | diag | A→A∧A | 対角射 |
| ∇A | codiag | A∨A→A | 余対角射 |
| evA B | ev | (A⊃B)∧A→B | 評価射 |
律子(りつし)に関しては「律子からカタストロフへ」を参照してください。
これらの射は、シーケント計算で言う公理シーケントとして使うことができます。例えば idA は、A → A というシーケントです。公理と基本リーズニング規則(シーケント計算の推論規則)という二本立てが嫌なら、公理シーケントは上段が空であるリーズニング規則とみなすことができます。
* ========[id] A → A
上段のアスタリスクは、「何もない」を明示する目印です。
対称性を表す射 σA B:A∧B→B∧A をリーズニング規則にするなら、
* ==============[symm] A∧B → B∧A
A∧B は A,B とカンマで書いてもいいので、
* ==============[symm] A,B → B∧A
でもかまいません。
あるいは、いわゆる“構造規則”として定式化する手もあります。
Γ,A,B,Δ → C ===============[exch] Γ,B,A,Δ → C
これは、換(exchange)構造規則です。
圏論的に自然なリーズニングの例 その1
実は、直積の対称性 A∧B → B∧A は、公理シーケントとして仮定する必要はなく、リーズニングで導き出すことができます。このとき、次の減(contraction)構造規則は仮定します。
Γ,A,A,Δ → C ===============[cont] Γ,A,Δ → C
対角射 ΔA:A→A∧A の存在が減(contraction)構造規則の根拠です。
A∧B → B∧A を導く(作り出す)リーズニングは次のようになります。
* * ==========[proj2] ===========[proj1] A∧B → B A∧B → A ==============================[prod] A∧B,A∧B → B∧A ==================[cont] A∧B → B∧A
上記のリーズニング図がリーズニング規則[symm]の定義になっていることは、デカルト閉圏Cにおいて次の等式が成立することに相当します。
- σA B = ΔA∧B;(π2A B∧π1A B)
リーズニング図の各段階における証明オブジェクトの式を書いてみると、このことが明らかになります。
* *
==========[proj2] ===========[proj1]
π2A B π1A B
==============================[prod]
π2A B∧π1A B
====================[cont]
ΔA∧B;(π2A B∧π1A B)
リーズニングの結果である最下段の証明オブジェクト ΔA∧B;(π2A B∧π1A B) を、自然演繹の証明図風に描くと次のようになります。
A∧B
--------------------[コピー]
A∧B A∧B
-----[∧除去2] -----[∧除去1]
B A
-------------------[∧導入]
B∧A
一番上の横線である[コピー]は、上段のモノを2つに増やすことです。この[コピー]は、最後のリーズニングステップである減(contraction)構造規則によって追加されたことに注意してください。
頑張って、自然演繹の証明図(の類似物)を証明オブジェクトとするリーズニング図を描いてみましょうか。
* *
========[proj2] ===========[proj1]
A∧B A∧B
----- -----
B A
=============================[prod]
A∧B A∧B
----- -----
B A
---------------
B∧A
=========================[cont]
A∧B
-----------------
A∧B A∧B
----- -----
B A
---------------
B∧A
こういう複合的な図は、場所を取るしめんどくさいので誰も描こうとしません。その結果、自然演繹ではリーズニングが暗黙的曖昧に扱われ、シーケント計算では証明オブジェクトがハッキリせず、自然演繹とシーケント計算の関係もモヤモヤのままとなります。残念なことです。
表現は色々あっても実体は同じ
直和を持つデカルト閉圏Cがありまして …… という所から話を始めると、式や絵による表現は色いろあるよね、ってことになります。
例えば、直積の第1射影 π1A B:A∧B→A は、自然演繹の推論図/証明図風に描けば次のようです(もう何度も出しました)。
A∧B -----[π1] A
ストリング図なら次のよう。
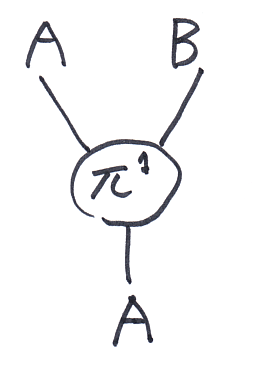
シーケント風なら、
- A∧B → A
単一の命題で書けば、
- A∧B⊃A
型付きラムダ式で書くなら、
- λ(x, y):A∧B.x
これらはいずれも“証明オブジェクト=圏Cの射の表現”なんです。既存の証明オブジェクトを加工したり組み合わせたりして新しい証明オブジェクトを作り出す行為・過程がリーズニングですけど、リーズニングにも色々な表現があります。
「感動か効率性か」に次のように書きました:
「同じもの」とは、同じ意味論的な対象物を指していて、表現としての構文が違うだけ、ということです。同じ意味論的な対象物とは、デカルト閉圏やその変形・拡張のことです。そうであるなら、同じ対象物に対する異なる構文を異なるままにしておく意義ってあるんでしょうか?
...[snip]...
そろそろ、歴史的な経緯は無視して、記法・用語法・定式化を統合してもいいんではないでしょうか。計算論と型理論と論理を別々に勉強して、それでやっとカリー/ハワード対応ではあまりにも大変過ぎます! 歴史や伝統に拘らなければいくらでもショートカットはあるでしょうに。
歴史や伝統を完全に無視するのは行き過ぎですが、「実体は同じ」だと知って、表現の多様性に惑わされないことも大事です。
圏論的に自然なリーズニングの例 その2
圏論的に自然なリーズニングをベースにしたとき、伝統的な自然演繹のリーズニングがどう書けるか、連言(∧)の除去規則と含意(⊃)の除去規則を例としてやってみます。
A → Y B → Y
=================[copair]
Γ → A∨B A∨B → Y
========================[comp]
Γ → Y
これは、伝統的な[∨除去]規則になります。証明オブジェクトとしての式も一緒に書くと次のようです。
g:A → Y h:B → Y
=====================[copair]
f:Γ → A∨B [g, h]:A∨B → Y
================================[comp]
f;[g, h]:Γ → Y
念のため、証明オブジェクトとして自然演繹の証明図風の図を使ったリーズニングも描いておきましょう(めんどくさいけど)。分かりやすいように、縦矢印の横に射の名前・式も添えておきます。
A B
--- ---
g↓ h↓
Y Y
===============[copair]
Γ A∨B
--- ----
f↓ [g, h]↓
A∨B Y
========================[comp]
Γ
---
f↓
A∨B
-----
[g, h]↓
Y
次は含意(⊃)の除去です。証明オブジェクトも添えたリーズニング図の1枚だけにします(色々描くの疲れた)。
f:Γ → A⊃B g:Δ → A *
========================[prod] =================[ev]
f∧g:Γ,Δ → (A⊃B)∧A ev:(A⊃B)∧A → B
=================================================[comp]
(f∧g);ev:Γ,Δ → B
これって、伝統的な[⊃除去]規則になってるでしょ。
僕が思っていたこと/思っていること
「自然演繹の証明図は静止画じゃダメ、アニメーションさせなきゃ!」とは、ずーっと思っていることです。2009年あたりにやっていたセミナーでは、そのアニメーションをホワイトボード上で実演していました。その状況を文字で伝えようとした次の記事では、「書き換える前/書き換えた後/もっと書き換えた後」のような見出し付きで何枚も証明図を出しています。
いわばパラパラ漫画の手法ですが、次の記事もパラパラ漫画=紙芝居で、絵や式の時間的変化を表現しようと試みています。
比較的最近(2016年2月)も、絵を描く様〈さま〉を連続的に写真に撮って証明オブジェクトの構成過程(リーズニング)を記録してみる実験をしてみたり。
ソフトウェアを使えば、ホワイトボードや紙を使わないでアニメーションを実現できるはずです。それをやるソフトウェアといえば -- 証明支援系ですよね。でも、現状の証明支援系のユーザーインターフェイスは、証明オブジェクトとリーズニングの可視化としてはとても貧弱な段階で不満があります。
「Coqの証明ゲームの表側と裏側 (誰も書かないCoq入門以前 4)」より:
- Coqシステムは、そして自分は、いったい何をやっているんだ?
- これが証明って、いったい何でだ?
こういう疑問を払拭できないのは、CoqのUIが貧弱なせいもあると思います。眼前の敵=モンスター=ゴールだけを表示するのは、バトルに没入するにはいいかも知れませんが、全般的な戦況が読めないのです。証明の現状を俯瞰的に眺めたいとか、出来上がった証明=終わった戦いを(時系列ではなくて)構造的に視覚化したいとかの要望に応える機能がありません。
Isabelleでも不満足な事情は同じです。Globularはなかなか良い視覚化のUIを持ってますが、別な意味で難しいソフトウェアです。と、そんな現状なので、ホワイトボードや紙から離れるのはまだ難しそうです。
この記事のサブタイトルを「圏論による再考」と付けました。自然演繹に対する再考は出来たと思います。でも、再構築には至っていません。自然演繹の圏論による再構築とはどんなものでしょうか?
まず、証明オブジェクトです。どんな種類の証明オブジェクトを選ぶかは多分に好みの問題ですが、僕はストリング図がいいと思います。ストリング図は、自然演繹の証明図にもラムダ式にも容易に変換できるし、視覚的直感に訴えます。「直感」というと厳密性に欠けるようですが、ストリンググラフにより組み合わせ構造を抽出できます。
証明オブジェクトとしてストリンググラフを使ったとき、リーズニングはグラフ書き換え(graph rewriting)となります。
この記事では、論理システム(論理を行うための形式的体系)のモデルとして直和を持つデカルト閉圏を使いましたが、もっと精密なモデル化には多圏(polycategory)が必要です。
ストリング図や多圏の話をこの記事に入れようかとも思いましたが、あまりにも長大になるのでやめました。いずれ別記事としてストリング図と多圏を準備した上で、自然演繹の再構築ができたらいいな、と思っています。
[追記]再構築の試み:
[/追記]
*1:セマンティクス駆動のほうが正しい気もしますが、語呂からセマンティックを使いました(セマンティックWebなんて言葉もあったりしたので)。semantic-drivenも誤用ではないようです。