このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

全称記号の導入規則について考える

雑記／備忘

昨日の記事「述語論理とインデックス付き圏と限量随伴性」で、述語論理のモデルの基本事項を述べたので、これを元にして、個別の話をチョビチョビしていくことにします。

自然演繹の悪口を書いた記事「自然演繹はちっとも自然じゃない -- 圏論による再考」で述語論理は扱わなかったので、自然演繹における「∀導入規則」について詮索（むしろダメ出し）します。

内容：

全称記号の導入と除去の規則

自然演繹の推論規則（の図）で、全称記号'∀'の導入（introduction）と除去（elimination）は次のような形です。

    P
 -------[∀導入]
  ∀x.P


   ∀x.P
 ----------[∀除去]
  P[x:=t]

まー、見た目は簡単です。「自然演繹はちっとも自然じゃない -- 圏論による再考」でも述べたことですが、自然演繹の推論図／証明図がロクデモナイ理由のひとつは、暗黙の前提が多すぎることです。暗黙の前提を知らない／慣れてない人には意味不明なオマジナイでしかありません。見た目が簡単だから簡単、なんてことはまったくありません！

記述されている部分以外に、証明図の仮定から問題の箇所に至る部分があります。そして、証明図の変形のbefore（変形前）とafter（変形後）があります。∀導入規則に相当する証明図の変形手順を以下に示します。Γは、証明図の最上段に現れる命題（述語、論理式）の並び（空な並びも認める）を表します。'↓'は省略している中間部分です。

before
  Γ
 ----
  ↓もともとあった証明図
   P

after
  Γ
 ----
  ↓新しい証明図
  ∀x.P

これでも意味不明ではありますが、あとでチャンとした変形手順を示すのでご安心を。ともかくも、beforeの証明図が描き変えられてafterの証明図になるのですが、述語論理の場合は、どの解釈領域上で議論しているかも明示すべきです。「述語論理とインデックス付き圏と限量随伴性」で述べた変数・型注釈の記法を使いましょう。

before
  Γ[x:X]
 ---------
  ↓
   P[x:X, y:Y]

after
  Γ[x:X]
 ---------
  ↓
  ∀w.P[x:X, w:Y]

Γ[x:X] = (Q1[x:X], ..., Qn[x:X]) だとして、Q[x:X] = Q1[x:X]∧ ... ∧Qn[x:X] とおけば、beforeは、“Q[x:X]からP[x:X, y:Y]に至る証明図”、afterは“Q[x:X]から∀w.P[x:X, w:Y]に至る証明図”だとしても（意味的には）かまいません。

before
  Q[x:X]
 ---------
  ↓
   P[x:X, y:Y]

after
  Q[x:X]
 ---------
  ↓
  ∀w.P[x:X, w:Y]

命題をどんな解釈領域上で考えているかを示す'on'記法も添えてみると：

before
  Q[x:X] on X
 -------------
  ↓
   P[x:X, y:Y] on X×Y

after
  Q[x:X] on X
 -------------
  ↓
  ∀w.P[x:X, w:Y] on X

アレレッ? X上だったりX×Y上だったり、証明図の変形により、命題の解釈領域も変化しています。いったいどうなっているの？

通常の自然演繹では、解釈領域を明示しないし、全称限量子の（意味的な）メカニズムも曖昧なままに、オマジナイとしての推論規則が与えられます。そりゃー、分かるわけないだろうよ。

証明ボックスを使った図示

もう少し事情がハッキリする図示法はないものか？ と探したら、少しだけマシな証明図の描き方を見つけました。"Natural deduction for predicate logic"（https://cs.uwaterloo.ca/~plragde/cs245old/06-prednd.pdf）というテキスト内で使われている次の図です。

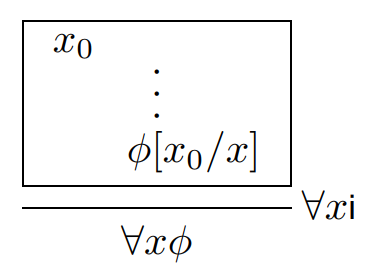
この図のミソは四角い箱で、証明ボックス（proof box）と呼びます。ボックス内に普通に証明（図）を描けますが、変数x0は、ボックス内でだけを使っていいローカルな自由変数です。ボックスが自由変数のスコープを提供するわけです。

しかし、自然演繹では（たぶん他の論理システムでも）スコープやローカル変数の概念がないので（遅れてるーっ）、他の箇所で出現してない新しい名前の変数（フレッシュ変数と呼ぶ）を導入します。キチンとしたブロックスコーピングがあるのなら、新しい名前じゃなくても大丈夫なんですけどね*1。

証明ボックス内で、フレッシュ変数x0を含む論理式（命題）φを結論とする証明図が描けたら、証明ボックスの外で∀x.φが証明されたことになります。フレッシュ変数（ローカル変数）x0を証明ボックスの外に持ち出すことは出来ないので、x0を全称束縛変数xに置き換えます。束縛変数は名前の影響を受けない（自由にα変換を行える）ので、x0とxは同じ名前でもいいのですが、リネームするのが無難です。

証明ボックスは閉じた環境ではないので、証明ボックスより上側にある命題は、ボックス内の証明の仮定として使ってかまいません。ローカル自由変数の使用が、ボックス内に制限されるだけです。

さて、証明ボックスをアスキーアート風に描いてみます（めんどくさいけど）。命題や変数の名前は我々の状況に合わせます。

  +---------------+
  |y              |
  |     :         |
  |   P[x:X, y:Y] |
  +---------------+
 -------------------[∀導入 y:=w]
   ∀w.P[x:X, w:Y]

yがローカル自由変数です。証明ボックスから外に出るとき、念のためにyをwにリネームしてから全称束縛しています。'y:=w'がリネームを表しています。

証明ボックスの上側に命題Q[x:X]があるなら、次のように描きましょう。

     Q[x:X]
     ↓
  +---------------+
  |y              |
  |     :         |
  |   P[x:X, y:Y] |
  +---------------+
 -------------------[∀導入 y:=w]
   ∀w.P[x:X, w:Y]

ローカル変数yを含まないQ[x:X]は、ボックスのなかに入れても影響はありません。

  +---------------+
  |y              |
  |   Q[x:X]      |
  |   ↓          |
  |   P[x:X, y:Y] |
  +---------------+
 -------------------[∀導入 y:=w]
   ∀w.P[x:X, w:Y]

今描いた証明図（のパターン）は、∀導入の後の状況なので、前後の変化を示すなら次のようになります。

before
     Q[x:X]
     ↓
  +---------------+
  |y              |
  |     :         |
  |   P[x:X, y:Y] |
  +---------------+

または
  +---------------+
  |y              |
  |   Q[x:X]      |
  |   ↓          |
  |   P[x:X, y:Y] |
  +---------------+

after
     Q[x:X]
     ↓
  +---------------+
  |y              |
  |     :         |
  |   P[x:X, y:Y] |
  +---------------+
 -------------------[∀導入 y:=w]
   ∀w.P[x:X, w:Y]

または
  +---------------+
  |y              |
  |   Q[x:X]      |
  |   ↓          |
  |   P[x:X, y:Y] |
  +---------------+
 -------------------[∀導入 y:=w]
   ∀w.P[x:X, w:Y]

要するに、ローカル自由変数yを持つ証明ボックス内で命題Pの証明が終わっている状況（証明ステート）があるのなら、次の状況ではPの全称束縛を下段に追加していいのです。

チャンとした∀導入の方法

冒頭に挙げた簡単な図（↓）で、∀導入の規則を説明しようなんて、所詮無理なんです。

    P
 -------[∀導入]
  ∀x.P

そもそも、自然演繹の証明図と推論規則は全然別なレベルの存在物で、同一の図示法で示そうなんてのが無茶もいいとこです。推論規則は与えられた証明図（証明オブジェクト、証明ステート）を変形する方法の記述なので、アニメーションで示す必要があります。

前節の証明ボックスのアイディアを踏まえて、さらに丁寧に証明図の変形過程を記述してみましょう。

step 0
   Q[x:X] on X

step 1
   Q[x:X] on X
                    +
                    |  [x:X, y:Y].Q[x] on X×Y

step 2
   Q[x:X] on X
                    +
                    |  [x:X, y:Y].Q[x] on X×Y
                    |  ------------------------
                    |     ↓ 証明 on X×Y
                    |  P[x:X, y:Y] on X×Y

step 3
   Q[x:X] on X
                    +
                    |  [x:X, y:Y].Q[x] on X×Y
                    |  ------------------------
                    |     ↓ 証明 on X×Y
                    |  P[x:X, y:Y] on X×Y
                    +
∀w.P[x:X, w:Y] on X

step 4
   Q[x:X] on X
  -------------
    |               +
    |               |  [x:X, y:Y].Q[x] on X×Y
    |               |  ------------------------
    |               |     ↓ 証明 on X×Y
    |               |  P[x:X, y:Y] on X×Y
    |               +
    ↓ 証明 on X
∀w.P[x:X, w:Y] on X

各ステップの左は、X上の命題や証明（図）を描く欄です。右に、X×Y上の命題や証明を描きます。前節の証明ボックスは、右側の部分を箱に入れて左側に“入れ子で押し込んだ絵”になっています。

変形手順を箇条書きで説明します。

  1. 最初に、X上の命題Q[x:X]がある。これは既に証明されているか、仮定する命題。
  2. Q[x:X]を、X×Y上の命題と解釈するためにダミー変数yにより変数水増しする。内容的には何も変わってないが、[x:X, y:Y].Q[x]はX×Y上の命題であり、しばらくX×Y上で議論が進む。
  3. [x:X, y:Y].Q[x]からP[x:X, y:Y]に至る証明（図）を、X×Y上で構成する。結果として、X×Y上では、[x:X, y:Y].Q[x]を仮定して[x:X, y:Y]を結論とすることが出来た。
  4. X×Y上の証明の結論を全称束縛してX上の命題を得る。念のために、自由変数yを束縛変数wにリネームしている。
  5. X×Y上の証明を根拠として、X上でも、Q[x:X]を仮定して∀w.P[x:X, w:Y]を結論とする証明が存在するとみなしてよい。

シーケントによるリーズニング記述

前節の説明で用いた絵のstep 4の右側は：

  [x:X, y:Y].Q[x] on X×Y
  ------------------------
     ↓ 証明 on X×Y
  P[x:X, y:Y] on X×Y

これを、横向きに書いて ([x:X, y:Y].Q[x] on X×Y)→(P[x:X, y:Y] on X×Y) としましょう。'on X×Y'をまとめて書いて、変数ごとの型宣言も省略すれば： [x, y].Q[x]→P[x, y] on X×Y 。この形を証明図に対応するシーケント（sequent）と呼びます。

絵のstep 4の左側は：

   Q[x:X] on X
  -------------
    ↓ 証明 on X
∀w.P[x:X, w:Y] on X

これをシーケントで表すなら Q[x]→∀w.P[x, w] on X です。

∀導入規則の要点は、[x, y].Q[x]→P[x, y] on X×Y という証明が存在するなら、Q[x]→∀w.P[x, w] on X という証明もあるぞ、という主張です。これを次のように書きましょう。

  [x, y].Q[x]→P[x, y]  on X×Y という証明が存在する
 =================================================== ならば
   Q[x]→∀w.P[x, w]  on X という証明が存在する

これは、特定のパターンの証明の存在から、もうひとつのパターンの証明の存在を保証するもので、リーズニング規則（reasoning rule）と呼びます。通常、シーケントの推論（図）と呼ばれますが、同じ「推論」「証明」といった言葉を使っていると話が混乱するばかりなので、「リーズニング」を使います。

日本語の補足文がうざいなら取り除いてもいいですが、分かりやすいので残しておきます。

全称限量随伴性と∀導入リーズニング規則

これでやっと、「述語論理とインデックス付き圏と限量随伴性」で述べた限量随伴性（quantification adjunction）を登場させる準備ができました。

XとYを集合として、直積の第一射影を π:X×Y→X とすると、πによる述語（述語と命題は同義語）の引き戻し π*:Pred[X]→Pred[X×Y] があるのでした。Xの述語（命題）Qに対するπ*(Q)は、変数水増しオペレーター[x, y].を用いて、

  • π*(Q) = [x, y].Q[x]

と書けます。π*の右随伴が∀πで、∀π(P)も変数を用いて書けます。

  • ∀π(P) = ∀w.P[x, w]

したがって、随伴 π* -| ∀π によるホムセット同型は次の形に書けます。

  • Pred[X×Y]([x, y].Q[x], P[x, y]) \stackrel{\sim}{=} Pred[X](Q[x], ∀w.P[x, w])

このことを次の形に書いてもよいでしょう。

  [x, y].Q[x]→P[x, y]  というPred[X×Y]の射が存在する
 ===================================================== ならば
   Q[x]→∀w.P[x, w]  on X というPred[X]の射が存在する

述語（命題）の圏の射とは、当該解釈領域上の証明（図）のことなので、

  [x, y].Q[x]→P[x, y]  on X×Y という証明が存在する
 =================================================== ならば
   Q[x]→∀w.P[x, w]  on X という証明が存在する

これは、∀導入のリーズニング規則そのものです。つまり、∀導入のリーズニング規則の根拠は、全称限量（universal quantification）の随伴性 π* -| ∀π だったのです。

冒頭に出した“見た目は簡単なオマジナイ”からは、背後にある構造を見通すことはまず無理でしょう。図の描き方や説明の仕方を、もうちょっとチャンとして欲しいものです。

*1:ブロック内の変数が外の変数を隠してしまうシャドーイングは、人間の間違いを誘発するので、常にフレッシュ変数を使うのもひとつの見識ではあります。