ジョン・バエズ(John C. Baez)が2010年に書いた短いノートに
というのがあります。このEveryoneって誰だよ? という気もしますが、まーともかく「誰でも」知っておくべき事として13個の定義が挙げられています。1番目は圏の定義で、13番目(最後)が圏のブレイド付きモノイド同値関手(ついでに対称モノイド同値関手も)です。そのひとつ前(12番目、最後から2番目)は、モノイド圏のあいだのモノイド同値(monoidal equivalence)関手です。
この記事では、バエズが12番目に取り上げたモノイド同値関手について紹介します。基本となるモノイド関手の概念と関連事項については次の記事で解説しています。
この記事でもモノイド関手の復習をします。
なお、この記事は、「自然演繹の再構築への道」で述べた計画の一環です。
内容:
各種のモノイド関手の呼び名
モノイド関手にはいくつかの種類があります。単に形容詞なしで「モノイド関手」と言ったときに何を意味するかは人により違います。以下に、モノイド関手の種類を挙げます。
- 厳密モノイド関手(strict monoidal functor): F(A
B) = F(A)
F(B) などの法則が等式として成り立つ。
- 強モノイド関手(strong monoidal functor): F(A
B)
F(A)
F(B) などの法則が同型として成り立つ。
- ラックス・モノイド関手(lax monoidal functor): F(A)
F(B) → F(A
B) などの法則を与える射が存在するが、同型とは限らない。
- 反ラックス・モノイド関手(oplax monoidal functor): F(A
B) → F(A)
F(B) などの法則を与える射が存在するが、同型とは限らない。
一時期(「緩関手、反緩関手、強関手、厳密関手とか、おぼえられねー」の頃)、"lax"を「緩」と訳してましたが、最近はカタカナ「ラックス」です。ちなみに、「おぼえられねー」悩みは、マッカーディのストライプ図により解消しました。
ラックス・モノイド関手と反ラックス・モノイド関手は、定義に登場する矢印の向きが逆になるという意味で双対です。反ラックス(oplax)の代わりに余ラックス(colax)を使うこともあります。laxにopだのcoだの付けるのではなくて、ラックス・コモノイド関手(lax comonoidal functor)がいいのではないか、という意見もあります。モノイド関手/コモノイド関手を使うなら、形容詞はラックス(lax)ではなくて弱(weak)でもいいかも知れません。
「強モノイド関手/弱モノイド関手/弱コモノイド関手」が一番辻褄があってる気がしますが、よく使われていると思われる「強モノイド関手/ラックス・モノイド関手/反ラックス・モノイド関手」を使うことにします。([追記]後で、「強」はやめて「タイト」を使うようになりました。「高次圏: 用語法と文脈(主に2次元) // 厳密、強、ラックス、反ラックス」参照。[/追記])
ここで定義するモノイド関手は、強モノイド関手(strong monoidal functor)と呼ばれることがありますが、これが標準的なモノイド関手だと思われるので特に形容詞は付けないことにします。
と書きましたが、曖昧さを避けるために今回は形容詞を常に付けます。
ストライプ図の復習
ラックス・モノイド関手は、2つのモノイド圏C, Dのあいだの関手Fの上に載る自然変換μ, εで構成された代数構造と考えたほうがいい、と「ラックス・モノイド関手について、もうちょっと」で注意しました。実際、自明なモノイド圏からモノイド圏Cへのラックス・モノイド関手はC内のモノイドになります。
マッカーディのストライプ図を使えば、モノイドとラックス・モノイド関手の類似性を視覚的に確認できます。ストライプ図については、「モノイド関手/ラックス・モノイド関手とその実例」で述べてますが、ここで復習しておきます。
この記事で採用する描画方向は ↓→ です。旗で示すならば:
次の図を見てください。
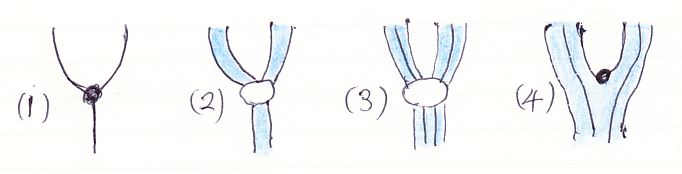
(1)は、モノイド乗法 m:AA→A を描いたものです。ワイヤーがA、黒丸が乗法mです。(2)は、それに厚みを付けたもの。乗法は白丸になっています。(3)は、厚み付きワイヤーを心線(芯線)と青い関手シースとして描いたものです。これが、ラックス・モノイド関手 (F, μ, ε) の乗法 μA,B:F(A)
F(B)→F(A
B) を表します。(4)は、μA,Bを小さな黒丸で代表させたものです。
次は単位に関する図です。
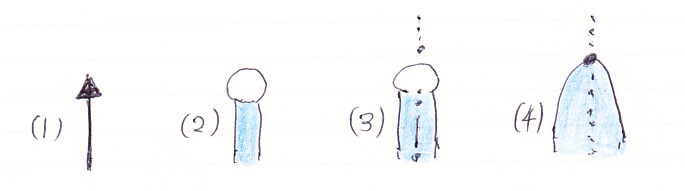
乗法の場合と事情は同じです。(1)は、モノイドの単位 e:I→A の図ですが、その後はラックス・モノイド関手 (F, μ, ε) の単位 ε:I→F(I) を表します。
状況設定
CとDをモノイド圏として、(F, μ, ε) と (G, ν, ι) を C→Dである2つのラックス・モノイド関手とします。この設定で、モノイド自然変換 ψ::(F, μ, ε)⇒(G, ν, ι):C→D を定義したいのですが、状況設定をもう少し詳しく述べます。
C = (C, , I), D = (D,
, I) とします。C, D はモノイド圏の構造全体の意味でも、台となる圏(underlying category)の意味でも使います(記号の乱用)。Cのモノイド積/単位対象と、Dのモノイド積/単位対象は別物なので、ほんとは別な記号で表すべきですが、同じ記号
, I を使い回しています(面倒だから)。
C, D は厳密とは限らないモノイド圏なので、それぞれに結合律子、左単位律子、右単位律子があります(律子(りつし)に関しては「律子からカタストロフへ」を参照してください)。これらの律子は明示されてませんが、必要があればそれらを α, λ, ρ で示します。Cの律子とDの律子は別物ですが、同じ記号 α, λ, ρ で書きます(面倒だから)。
F:C→D は関手で、μ::(F×F)⇒F
:C×C→D は自然変換、εは I→F(I) in D という射です。εも自然変換と呼ぶことがありますが、定数関手 KI(A) = I からもうひとつの定数関手 KF(I)(A) = F(I) への自然変換と考えることができるからです。
μ::(F×F)⇒F
が自然変換であることは次のように図示できます。青いストライブ内の2つのオダンゴは、f:A→B, g:C→D in C で、(F(f)
F(g));μB,D = μA,C;F(f
g) を示しています。
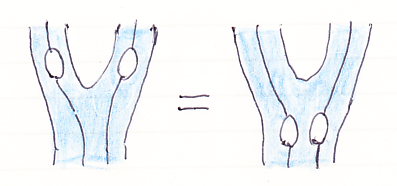
ラックス・モノイド関手の法則は、マッカーディのストライプ図で次のように描けます。
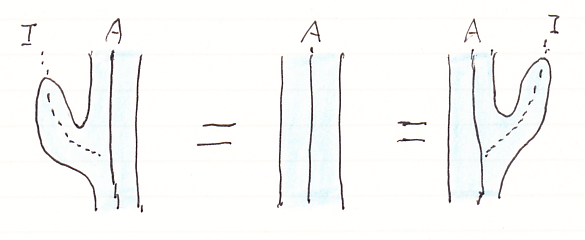
関手Fと自然変換μ, εに関して、この図を等式に書き下しましょう。律子 α, λ, ρ も考慮した形にします。
結合律 左辺:
(F(A)F(B))
F(C) ↓ μA,B
F(C) F(A
B)
F(C) ↓ μA
B,C F((A
B)
C) ↓ F(αA,B,C) F(A
(B
C))
結合律 右辺:
(F(A)F(B))
F(C) ↓ αF(A),F(B),F(C) F(A)
(F(B)
F(C)) ↓ F(A)
μB,C F(A)
F(B
C) ↓ μA,B
C F(A
(B
C))
- 結合律 等式:(μA,B
F(C));μA
B,C;F(αA,B,C) = αF(A),F(B),F(C);(F(A)
μB,C);μA,B
C
左単位律 左辺:
IF(A) ↓ε
F(A) F(I)
F(A) ↓μI,A F(I
A) ↓F(λA) F(A)
左単位律 右辺:
IF(A) ↓λF(A) F(A)
- 左単位律 等式: (ε
F(A));μI,A;F(λA) = λA
右単位律も同様で、
- 右単位律 等式: (F(A)
ε);μA,I;F(ρA) = ρA
(G, ν, ι) がもうひとつのラックス・モノイド関手なら、文字を置き換えただけの次の等式が成立します。
- 結合律 等式:(νA,B
G(C));νA
B,C;G(αA,B,C) = αG(A),G(B),G(C);(G(A)
νB,C);νA,B
C
- 左単位律 等式: (ι
G(A));νI,A;G(λA) = λA
- 右単位律 等式: (G(A)
ι);νA,I;G(ρA) = ρA
モノイド自然変換
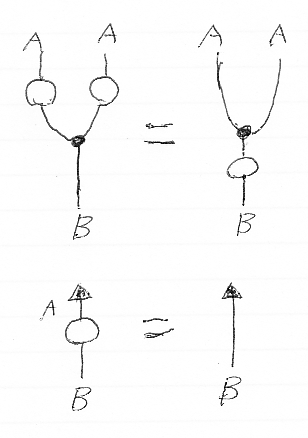
ラックス・モノイド関手のあいだのモノイド自然変換(monoidal natural transformation)は、モノイドの準同型写像の類似物です。気分としては、次の“比例式”が成立します。
- モノイド : モノイドの準同型写像 = ラックス・モノイド関手 : モノイド自然変換
(A, m, e), (B, n, i) がモノイド圏内の2つのモノイドとして、f:A→B がモノイドの準同型写像なら、次の等式が成立します。
- (f
f);m = m;f
- e;f = i
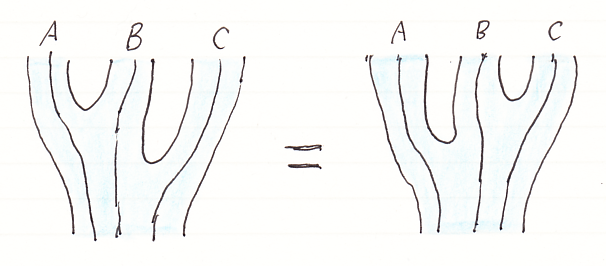
絵に描けば次のようです。
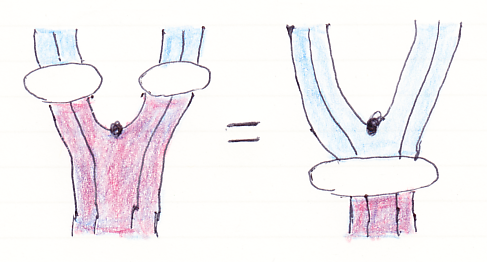
これをヒントに、モノイド自然変換 ψ::(F, μ, ε)⇒(G, ν, ι) の絵を描きましょう。ここで、(F, μ, ε) と (G, ν, ι) はラックス・モノイド関手です。絵で、青い関手シースがFを表し、紫(青に赤を上塗り)の関手シースがGを表します。白いオダンゴがψです。
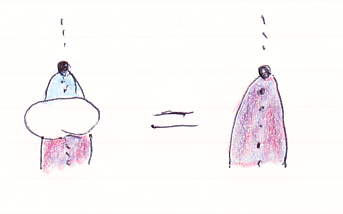
絵を見ながら等式に書き下します。
- ψA
ψB;μA,B = μA,B;ψA
B
- ε;ψI = ι
これらの等式が、自然変換 ψ::F⇒G:C→D がモノイド自然変換であるための条件です。
ψがモノイド自然変換で、すべての成分 ψA:F(A)→G(A) in D が同型(可逆)であるとき、モノイド自然同型(monoidal natural isomorphism)と呼びます。(F, μ, ε) と (G, ν, ι) がモノイド自然同型で結ばれるとき、これらのラックス・モノイド関手は同じだとみて差し支えありません。
モノイド同値関手
DとCがモノイド圏で、F:C→D, G:D→C がラックス・モノイド関手とします。ラックス・モノイド関手どうしの結合は再びラックス・モノイド関手になりますから(これは証明を要することですが)、GF:C→C, F
G:D→D はラックス・モノイド関手です。
は、関手の反図式順結合です。常に図式順結合を使っている僕が、ここだけ反図式順にしているのはちょっとした事情がありますが、まーそれはいいとしましょう。
FとGが次の等式を満たすとき、互いに逆(inverse)になります。
- G
F = IdC
- F
G = IdD
しかし、逆は強すぎる条件なので、イコールをモノイド自然同型に弱くします。この場合は、互いに弱逆(weak inverse)となります。つまり、FとGが互いに弱逆とは:
- モノイド自然同型 ψ::G
F⇒IdC:C→C が存在する。
- モノイド自然同型 φ::F
G⇒IdD:D→D が存在する。
弱逆を持つようなラックス・モノイド関手をモノイド同値関手(monoidal equivalence functor)と呼びます。冒頭で引用したバエズの定義では、強モノイド関手に限定してモノイド同値を定義していますが、定義の形はラックス・モノイド関手でも強モノイド関手でも変わりません。要するに、弱可逆な関手です。
2つのモノイド圏が、弱可逆なモノイド関手(ラックス・モノイド関手または強モノイド関手)で結ばれているなら、その2つのモノイド圏を区別する必要がないことを意味します。あるモノイド圏Cが扱いにくいとき、同値なモノイド圏Dを代わりに使っても、本質的な差異は生じないのです。