ベックの分配法則の事例と計算法 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ここんところ「モナドのお勉強をしましょう」というゆるいシリーズ記事（番号とかは付けてない）を書いているのですが、今日はベックの分配法則の例を挙げます。

内容：

リストモナドとバッグモナド
ベックの分配法則
随伴系から作られるモナド達
分配法則の具体的な記述
その他の分配法則

リストモナドとバッグモナド

今回主に使うモナドは、（毎度おなじみの）集合圏Set上のリストモナド〈list monad〉 List = (List, η^List, μ^List) です。それと、集合Aからバッグ〈有限マルチセット〉の集合を作るバッグモナド〈bag monad〉 Bag = (Bag, η^Bag, μ^Bag) も考えます。その他の例は後で出します。

a₁, ..., a_n∈A に対して、これらの要素のリストは [a₁, ..., a_n] と書きます。これらの要素のバッグは、区切り記号を';'にして、[a₁; ...;a_n] と書くことにします（とりあえずの記法）。リストとバッグ（それと有限集合）の違いは：

リストは順序が問題になるが、バッグは順序を問題にしない。[1, 2, 2] ≠ [2, 1, 2] だが、[1; 2; 2] = [2; 1; 2] である。
バッグは、有限集合とは違って、重複に意味がある。{1, 2, 2} = {1, 2} だが、[1; 2; 2] ≠ [1; 2] である。

リストもバッグも長さ（サイズ）を持つので、aの長さを |a| と書きます。空リスト／空バッグの長さは0です。モナドの構造を与える演算は：

η^List:A→List(A) in Set は、Aの要素からシングルトン・リストを作る演算。
μ^List_A:List(List(A))→List(A) in Set は、入れ子のリストを平坦にする演算。
η^Bag:A→Bag(A) in Set は、Aの要素からシングルトン・バッグを作る演算。
μ^Bag_A:Bag(Bag(A))→Bag(A) in Set は、入れ子のバッグを平坦にする演算。

これらが、モナドの結合律と左右の単位律を満たすことは練習問題ですが、計算法（のヒント）はこの記事の後のほうで説明しています。

ベックの分配法則

LとMが圏C上のモナドのとき、ベックの分配法則〈Beck's distributive law〉とは、次の形の自然変換で、とある条件を満たすものです。

δ::M*L⇒L*M:C→C

ここで、'*'は図式順結合であることに注意してください。反図式順で書くなら：

δ::L・M⇒M・L:C→C

なんで「分配法則」と呼ぶかは、L = List, M = Bag の例を考えるといいでしょう。ListとBagに関する分配法則δがあったとして、成分で書くと：

For A∈|Set|,
δ_A:List(Bag(A))→Bag(List(A)) in Set

となります。Bag(A)の要素 a = [a₁; ...; a_n] は、足し算 a₁ + ... + a_n のようなものだと考えます。List(Bag(A))の要素は、 [b₁, ..., b_m] で、b_i は、

(b_i)_{j_i} = a_{i,j_i} （1 ≦ j_i ≦ n_i, n_i = |b_i|）

のように、二重インデックス族（行列とはちょっと違う） a_{i,j_i} で書けます（詳細は後述）。

リスト [b₁, ..., b_m] を、b₁, ..., b_m の掛け算（積）とみなしましょう。すると：

δ_A:(Aの要素を足し算したものを掛け算したもの) |→ (Aの要素を掛け算したものを足し算したもの)

となります。これは、“和の積”を“積の和”に展開する操作なので、分配法則による式変形（多項式計算）だと言っていいでしょう。

ベックの分配法則のより詳しいことは、以下の記事に書いてあります。なお、当時（2007年）は「ベックの法則」と呼んでいました。最近はやっぱり「分配」を付けたほうが混同を避けられると思ってます。記法も当時と最近では若干違います。

ベックの法則と複合モナド

ベックの分配法則では、モナドLとモナドMの役割が違うので、

δは、Mに対するLの分配法則〈distributive law of L over M〉

と呼ぶことにします。通常の分配法則は「足し算に対する掛け算の分配法則〈The distributive law of multiplication over addition〉」なので、不自然な言い方ではないでしょう。

随伴系から作られるモナド達

次のような圏を考えます。

Mon ：モノイドとモノイド準同型射の圏
CMon ：可換モノイドとモノイド準同型射の圏
ICMon ：ベキ等可換モノイドとモノイド準同型射の圏
Pted ：付点集合〈pointed set〉と付点を保つ写像の圏
SRng ：半環（掛け算が可換とは限らない）と半環の準同型射の圏
ISRng ：足し算がベキ等な半環と半環の準同型射の圏
MonZ ：零〈吸収元 | absorbing element〉を持つモノイドとモノイド準同型射の圏

これらの圏の対象は、集合になんらかの構造を載せた構造付き集合〈structured set〉です。なので、構造付き集合にその台集合〈underlying set〉を対応させる忘却関手 U_C:C→Set を持ちます。以下、圏Cが何であっても、忘却関手 U_C を単にUと書きます。

上記の圏の忘却関手は、随伴の左パートナー〈左随伴関手〉 Free_C:Set→C を持ち、随伴系 (η, ε: Free_C -| U, Free_C:Set→C) が存在します。今使った随伴系の書き方は、「随伴に関する注意事項 // 随伴系の方向」で説明しています。忘却関手の左パートナーは自由生成関手と呼びます。

随伴系があれば、それからモナド (Free_C*U, η, Free_C*ε*U) を作れます。ここで、'*'は関手の図式順結合記号です。次は、上記の圏と随伴系から作ったモナドの一覧です。

圏	自由生成関手	モナドの名前
Mon	FreeMon	List
CMon	FreeCMon	Bag
ICMon	FreeICMon	FinPow（有限ベキ集合）
Pted	FreePted	Maybe, Pt（付点）
SRng	FreeSRng	NCPoly（非可換多項式）
ISRng	FreeISRng	INCPoly（ベキ等非可換多項式）
MonZ	FreeMonZ	ListZ（零付きリスト）

それほど馴染みがないと思われる下の3つのモナドの台関手を簡単に説明します。

non-commutative polynomials NCPoly(A) ：集合Aの要素を不定元として、係数なし（強いて言えば自然数係数）で構成された形式的多項式の集合。掛け算の可換性は仮定しない。
(additively-)idempotent non-commutative polynomials INCPoly(A) ：上記の非可換多項式において、足し算をベキ等だとしたもの。
lists with zeros ListZ(A) ： List(A)∪{⊥}、通常のリスト以外に、特殊な要素⊥（連接の吸収元になる）を追加した集合。

今挙げた随伴系・モナド以外に、可換半環でパラメトライズ（インデキシング）された随伴系・モナドの族を紹介します。Rを可換半環として、R上の加群（左右の別はない）と加群準同型射の圏をMod_Rとします。引き算ができるとは限らないので、正確には半加群ですが、めんどうなので加群と呼んでしまいましょう。Mod_Rも構造付き集合の圏なので、忘却関手と自由生成関手による随伴系を構成できます。

(η, ε: FreeMod_R -| U, FreeMod_R:Set→Mod_R)

FreeMod_R(A) は、Aから生成されたR上の（あるいはR係数の）自由加群（自由に生成された加群）と呼びます。随伴系からモナドが構成できるので、モナドの表に追加すれば：

圏	自由生成関手	モナドの名前
Mod_R	FreeMod_R	LinComb_R（R-線形結合）

LinComb_R(A) は、集合Aの要素達のR係数形式的線形結合〈formal linear combination over R〉の全体です。これは、R係数の1次式を計算するモナドです。可換半環Rを可換環にとれば、通常の加群の議論になり、体にとればベクトル空間の議論になります。

バッグモナドBagと有限ベキ集合モナドFinPowは、可換半環を使った記述が可能です。

Bag(A) $\stackrel{\sim}{=}$ LinComb_N(A) = U(FreeMod_N(A)) in Set
FinPow(A) $\stackrel{\sim}{=}$ LinComb_B(A) = U(FreeMod_B(A)) in Set

ここで、Nは自然数の半環、Bは{0, 1}に 1 + 1 = 1 と足し算を入れた半環です。バッグモナドは、N係数1次式のモナドと同じであり、有限ベキ集合モナドは、B係数1次式のモナドと同じです。

分配法則の具体的な記述

リストモナド、バッグモナド、有限ベキ集合モナドは、コレクション（モノの集まり）データ型を構成するモナドです。しかしながら、モナドの由来となる随伴系を見ると、代数的構造に対する自由生成-忘却スタイルの随伴系になっています。起源が代数的なので、計算も代数的になります。

δ::Bag*List⇒List*Bag:Set→Set を、バッグモナドに対するリストモナドの分配法則だとして、δを具体的に記述することを考えます。バッグ [a₁; ...; a_n] は形式的足し算 a₁ + ... + a_n で、リスト [a₁, ..., a_n] は形式的掛け算 a₁・... ・a_n のことだと思いましょう。ここでの形式的とは、「形だけの」という意味で、[2; 3; 3] を 2 + 3 + 3 と書いても、8 と値を算出することはしないのです。あくまで「式（形式）」であって、「値（算出値）」は考えません。

バッグは足し算〈和〉、リストは掛け算〈積〉とみなすので、次のように書けます。

$[a_1;\:...;\: a_n] \:=\: \sum_{i = 1}^{n}a_i$
$[a_1,\:...,\: a_n] \:=\: \prod_{i = 1}^{n}a_i$

バッグのリスト、つまり“和の積”を書き下しましょう。幾つかのバッグ〈和〉をギリシャ文字αと添字番号を使って、α₁, ..., α_n とすると、それらのリスト〈積〉は：

$[\alpha_1,\:...,\: \alpha_n] \:=\: \prod_{i = 1}^{n}\alpha_i$

各 i ごと（1 ≦ i ≦ n）の α_i は：

$\alpha_i \:=\: [(\alpha_i)_1;\:...;\: (\alpha_i)_{n_i}] \:=\: \sum_{j_i = 1}^{n_i}(\alpha_i)_{j_i}$

したがって、

$[\alpha_1,\:...,\: \alpha_n] \:=\: \prod_{i = 1}^{n}\sum_{j_i = 1}^{n_i}(\alpha_i)_{j_i}$

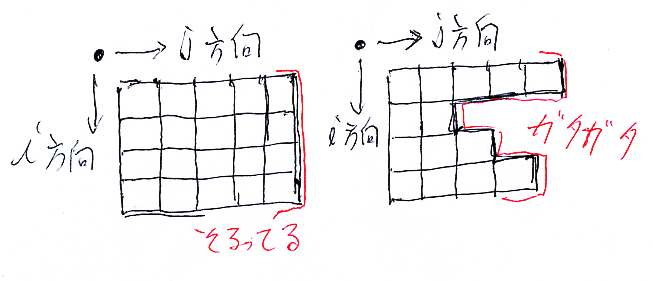
$\alpha_{i, j_i} \: :=\: (\alpha_i)_{j_i}$ と置くと、 $\alpha_{i, j_i}$ は二重インデックス族ですが、行列とは違って、インデックスセットが（必ずしも）矩形にはなりません。j の動く範囲が i ごとに変化するので、インデックスセットの形がガタガタです。

記述を簡略にするためにインデックスセットに名前を付けておきましょう。

I := {1, ..., n}
J_i := {1, ..., n_i}, n_i = |α_i|

iが動く範囲がIで、j_iが動く範囲がJ_iです。この記号を使うと：

$[\alpha_1,\:...,\: \alpha_n] \:=\: \prod_{i \in I}\sum_{j_i \in J_i}\alpha_{i, j_i}$

ちょっと簡略になりました。この“和の積”が、“積の和”に変形されます。

“積の和”の記述のために、マルチインデックスを準備します。太字のインデックス j は、J_i 達の直積集合 J := J₁×...×J_n を走るとします。j = (j₁, ..., j_n), j_i∈J_i 。マルチインデックスを使って“積の和”を書けば：

$\sum_{{\bf j}\in {\bf J}} \prod_{i \in I}\alpha_{i, j_i}$

分配法則が成立するなら、“和の積”と“積の和”が等しいので、

$\prod_{i \in I}\sum_{j_i \in J_i}\alpha_{i, j_i} \:=\: \sum_{{\bf j}\in {\bf J}} \prod_{i \in I}\alpha_{i, j_i}$

これが、分配法則の一般的な形です。j を (j₁, ..., j_n) に展開して書いたほうが見やすいかも知れません。

$\prod_{i \in I}\sum_{j_i \in J_i}\alpha_{i, j_i} \:=\: \sum_{(j_1, ..., j_n)\in {\bf J}} \prod_{i \in I}\alpha_{i, j_i} \,,\: {\bf J} = \prod_{i = 1}^{n}J_i$

δ_A:List(Bag(A))→Bag(List(A)) in Set の具体的な記述は、[α₁, ..., α_n]∈List(Bag(A)) に対して、

$\delta_A([\alpha_1,\: ...,\:\alpha_n]) \:=\: \delta_A(\prod_{i \in I}\sum_{j_i \in J_i}\alpha_{i, j_i}) \: :=\: \sum_{(j_1, ..., j_n)\in {\bf J}} \prod_{i \in I}\alpha_{i, j_i}$

総和記号は形式的な和（つまりバッグ）、総積記号は形式的な積（つまりリスト）と解釈します。

バッグモナドに対するリストモナドの分配法則が、ベックの分配法則の公理（分配法則の法則）を満たすことを具体的に確認するときは、今述べた具体的な表示を使って具体的に計算します。結果は当たり前のことなんですが、一回は確認する必要があります。

その他の分配法則

今まで説明した、Bagに対するListの分配法則を δ^Bag,List と書きましょう。他にも（ベックの）分配法則があるからです。

δ^Bag,List とほとんど同じ構成で、有限ベキ集合モナドFinPowに対するListの分配法則 δ^FinPow,List を定義できます。

Maybeモナド（付点モナド）に対しても、Listの分配法則があります。δ^Maybe,List_A:List(Maybe(A))→Maybe(List(A)) は、⊥をひとつでも含むリストはすべて⊥にしてしまう写像として定義できます。

これで3つの（ベックの）分配法則が定義できました。

δ^Bag,List::Bag*List⇒List*Bag:Set→Set
δ^FinPow,List::FinPow*List⇒List*FinPow:Set→Set
δ^Maybe,List::Maybe*List⇒List*Maybe:Set→Set

これらの分配法則は、モノイドの圏Mon上のモナドに“持ち上がり”ます。さらに、集合圏Set上のモナドへと“引き戻せ”ます。その結果、分配法則とSet上のモナドは、次のように対応します。

分配法則	Set上のモナド
δ^Bag,List	NCPoly
δ^FinPow,List	INCPoly
δ^Maybe,List	ListZ

“持ち上げ”や“引き戻し”に正確な意味を与えるには、モナドと随伴の一般論が必要ですが、一般論の前に事例を知っていれば理解の助けになるでしょう。

[追記]引き戻しに関しては、「リストモナドとテンソル空間モナドのあいだの準同型射 // モナドを随伴系に沿って引き戻す」に書いてありました。[/追記]