フリーモナド 1：自由で無料な木 - 檜山正幸のキマイラ飼育記 (はてなBlog)

フリーモナドの「フリー」は、「自由」の意味と共に「ただ〈for free〉」の意味もあります。「ただで手に入るモナド」ということです。しかし、この「ただで」は、「課金したらガチャをただで引けるよ」の「ただで」と同じで、事前のコストはかかっています。

事前のコストとは、「モナドがただで手に入る」環境を構築する手間です。この環境の説明／モナド入手法の説明には、多くの場合、HaskellコードまたはHaskell風擬似コードが使われています。プログラミング言語としてのHaskellの利便性が、当該メカニズムの圏論的内実を抽出するときにはむしろ仇になります。それで苦労している人へのアドバイス／解説がこの記事の内容です。

ここでは、（比較的普通の）圏論の概念・語法・記法により、モナドがただで手に入る状況をセットアップします。ここで行うセットアップが、「モナドをただで手に入れる」ための初期課金なのですが、それは安いでしょうか？高いでしょうか？$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\twoto}{ \Rightarrow}
\newcommand{\Up}[1]{ \overline{#1} }
\newcommand{\Dwn}[1]{ \underline{#1} }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\Imp}{\Rightarrow }
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
%`$

内容：

はじめに
どこの誰？
モノイドとモナド
忘却と増強
増強の繰り返しと増強の拡張
フリーモナドは自由なのか
フリーモナドはツリーモナド
もっとツリーモナド
帰納的な生成規則

はじめに

冒頭に述べたような動機で記事を書き始めたのですが、思いの外長くなってしまいました。区切りのいいところで一旦切って、2回に分けます。この記事を「1」として、引き続く記事は「2」とします。圏論的な不動点方程式と、不動点方程式によるフリーモナドの構成については「2」で述べます。

どこの誰？

この記事では、何人か（擬人法）の登場人物が出てきます。それらの登場人物（概念）が“どこの誰”かが分からないと、理解が不明瞭になりがちです。「どこ」とは、概念的事物達の棲息地ですが、集合や関数なら集合圏 $`{\bf Set}`$ に棲んでいます。$`F:{\bf Set} \to {\bf Set}`$ が関手だとすると、この関手は（サイズの制限から）集合圏には居られません。$`F`$ の棲息地は、大きな圏も許す圏の2-圏 $`{\bf CAT}`$ です。

$`\quad F:{\bf Set} \to {\bf Set} \In {\bf CAT}`$

集合圏の自己関手のあいだの自然変換も同じ2-圏内に棲んでいます。

$`\quad \alpha :: F\twoto G : {\bf Set} \to {\bf Set} \In {\bf CAT}`$

集合圏の対象達からなる大きな集合や、集合圏の自己関手の対象パート〈object part〉は、大きな集合も許す集合圏 $`{\bf SET}`$ のなかに居ます。

$`\quad |{\bf Set}| \in |{\bf SET}|\\
\For F:{\bf Set} \to {\bf Set} \In {\bf CAT}\\
\quad F_\mrm{obj} : |{\bf Set}| \to |{\bf Set}| \In {\bf SET}
%`$

概念的事物としての圏には次元とサイズがあります。特定の次元とサイズを持った圏〈n-圏〉達が集まった“世界”〈棲息地〉を、次のような名前で記します。

	サイズ小さい	サイズ大きい	サイズとても大きい
次元 0	$`{\bf Set}`$	$`{\bf SET}`$	$`\mathbb{SET}`$
次元 1	$`{\bf Cat}`$	$`{\bf CAT}`$	$`\mathbb{CAT}`$
次元 2	$`2{\bf Cat}`$	$`2{\bf CAT}`$	$`2\mathbb{CAT}`$

より詳しくは「実用圏論： 2-圏、居住関係、プロファイリング」参照。

モノイドとモナド

今回の主題のひとつであるモナドと“モナドの圏”を定義しておきましょう。

圏 $`\cat{C}`$ は（必ずしも対称〈symmetric〉とは限らない）モノイド圏とします。記号の乱用で
$`\quad \cat{C} = (\cat{C}, \otimes, \mrm{I})`$
と書きましょう。モノイド圏 $`\cat{C}`$ 内のモノイド対象〈monoid object〉とモノイド準同型射〈monoid homomorphism〉からなる圏を $`\mrm{Mon}(\cat{C})`$ と書きます。特に：

$`\quad {\bf Mon} := \mrm{Mon}({\bf Set}) = \mrm{Mon}( ({\bf Set}, \times, {\bf 1}) )
\;\in |{\bf CAT}|
%`$

2つの圏 $`\cat{C}, \cat{D}\in |{\bf CAT}|`$ に対して、ホム圏 $`{\bf CAT}(\cat{C}, \cat{D})`$ を2-圏 $`{\bf CAT}`$ の対象とみなしたもの〈指数対象〉を、
$`\quad [\cat{C}, \cat{D}] \in |{\bf CAT}|`$
と書きます。そう、関手圏ですね。

ところで、ブラケット記法は、集合圏の指数対象、つまり集合のあいだの関数集合に対しても使います。紛らわしいときは、ブラケットに下付きの 1, 0 を付けます。

$`{\bf CAT}(\cat{C}, \cat{D}) = [\cat{C}, \cat{D}]_1`$ 下付きの 1 は、指数対象が1-圏〈通常の圏〉であることを示す。
$`{\bf Set}(A, B) = [A, B]_0`$ 下付きの 0 は、指数対象が0-圏〈集合〉であることを示す。

関手圏の対象（つまり関手）達の集合とホムセットは次のようにも書きます。

$`\quad \mrm{Ftor}(\cat{C}, \cat{D}) := |[\cat{C}, \cat{D}]| = |{\bf CAT}(\cat{C}, \cat{D})|\\
\For F, G \in \mrm{Ftor}(\cat{C}, \cat{D})\\
\quad \mrm{Nat}(F, G) := [\cat{C}, \cat{D}](F, G) = {\bf CAT}(\cat{C}, \cat{D})(F, G)
%`$

任意の圏 $`\cat{C} \in |{\bf CAT}|`$ に対して、その自己関手圏 $`[\cat{C}, \cat{C}]`$ は関手の結合／自然変換の横結合を（非対称な）モノイド積としてモノイド圏になります。記号の乱用で
$`\quad [\cat{C}, \cat{C}] := ([\cat{C}, \cat{C}], *, \mrm{Id}_\cat{C})`$
と書きましょう。$`*`$ は関手の結合／自然変換の横結合の図式順演算記号です（「関手と自然変換の計算に出てくる演算子記号とか // 今後使う予定の演算子記号」参照）。

ここでは、モノイド圏 $`[\cat{C}, \cat{C}]`$ 内のモノイド達の圏を、 $`\cat{C}`$ 上のモナドの圏〈category of monads over $`\cat{C}`$〉とします*1。このモナドの圏の射は、モナド準同型射〈monad homomorphism〉と呼びます。

$`\quad \mrm{Mnd}(\cat{C}) := \mrm{Mon}([\cat{C}, \cat{C}]) = \mrm{Mon}( ([\cat{C}, \cat{C}],*,\mrm{Id}_\cat{C}) ) \;\in |{\bf CAT}|
%`$

そして、$`\cat{C} = {\bf Set}`$ と置いたものが我々が扱うモナドの圏〈the category of monads〉です。

$`\quad {\bf Mnd} := \mrm{Mnd}({\bf Set}) := \mrm{Mon}([{\bf Set}, {\bf Set}]) = \\
\qquad \mrm{Mon}( ([{\bf Set}, {\bf Set}], *, \mrm{Id}_{\bf Set} ) ) \;\in |{\bf CAT}|
%`$

忘却と増強

この節と次の節では、Haskell風型クラスに関する注意を述べます。

去年〈2021年〉の記事「型クラスと忘却・追憶構造」では、忘却関手の部分的な逆を追憶〈reminiscent〉と呼んでいました。忘れたものを思い出すイメージからです。が、実際には、土台となる素材〈underlying thing〉に対して、パーツを付け足して目的の構造物を作り出すことが多いので、増強に変えます。

忘却関手の一般的な定義はありませんが、なにかしら忘却関手と呼ばれる関手 $`U:\cat{C} \to \cat{D} \In {\bf CAT}`$ があったとき、$`\cat{D}`$ の部分圏で定義された $`U`$ のセクションを増強関手〈enhancement functor〉、あるいは単に増強〈enhancement〉と呼ぶことにします。$`E`$ が $`U`$ の増強である条件は：

$`\For U:\cat{C} \to \cat{D}\In {\bf CAT}, E: \cat{D} \supseteq \cat{I} \to \cat{C} \In {\bf CAT}\\
\quad \mrm{IsEnhancementOf}(E, U) :\Iff E * U = \mrm{Id}_{\cat{I}} : \cat{I} \to \cat{I} \In {\bf CAT}
`$

$`U`$ とその増強 $`E`$ のペアが忘却・増強構造（以前の忘却・追憶構造、今回少し単純化している）です。忘却関手の文字 'U' は underlying thing からです。「underlying だから underline」という駄洒落から、次の記法も使います。

$`\For f:X \to Y \In \cat{C}\\
\quad \Dwn{X} := U(X),\, \Dwn{Y} := U(Y)\\
\quad \Dwn{f} := U(f) : \Dwn{X} \to \Dwn{Y} \In \cat{D}
%`$

$`U`$ の（部分的な）逆 $`E`$ は overline とします。

$`\For g:S \to T \In \cat{I}\\
\quad \Up{S} := E(S),\, \Up{T} := E(T)\\
\quad \Up{g} := E(g) : \Up{S} \to \Up{T} \In \cat{C}
`$

Haskell風記法の場合、型クラスの機能により、忘却・増強が暗黙に適用され、異なる対象物に同じ名前を使えます。これはとても便利ですが、同じ名前を使い回すので、名前が指している対象物〈デノテーション〉が“どこの誰”か分からなくなる弊害もあります。ここでは（続く記事では）、煩雑になるのは承知の上で、明示的に忘却・増強をします。

増強の繰り返しと増強の拡張

Haskell風型クラスは、モデル論の指標と似てますが、増強定義のフレームワークと見たほうがいいでしょう。この点をこの節で説明します。より詳しい説明は「型クラスと忘却・追憶構造」にあります。

class Semigroup a where
  (<>) :: a -> a -> a
  -- 二項演算の結合法則は書けない（が、想定する）

class Semigroup a => Monoid a where
  mempty :: a
  -- 右単位法則と左単位法則はは書けない（が、想定する）

↑これは、以下の指標と類似しています（指標については「指標と不完全インスタンス」）。

signature SingleSet {
  sort A in Set
}

signature Semigroup extends SingleSet {
  operation (<>) : A×A → A in Set
  // 二項演算の結合法則は省略
}

signature Monoid extends Semigroup {
  operation mempty : 1 → A in Set
  // 右単位法則と左単位法則は省略
}

上の指標の（関手意味論による）モデルの圏を考えると、次のような忘却関手の系列が得られます。

$`\quad \mrm{Model}(\text{Monoid}) \overset{U_2}{\to}
\mrm{Model}(\text{Semigroup}) \overset{U_1}{\to}
\mrm{Model}(\text{SingleSet})
%`$

$`\mrm{Model}(\text{SingleSet})`$ を集合圏と同一視して、モデルの圏にボールド体の固有名を付けると：

$`\quad {\bf Mon} \overset{U_2}{\to}
{\bf Semigrp} \overset{U_1}{\to}
{\bf Set}
%`$

忘却関手に対する増強は以下のようになります。$`\leftarrow\!\subseteq`$ は部分的に定義された関手を意味します（方向が逆なのは、特に意味はありません）。

$`\quad {\bf Mon}\; \overset{E_2}{\leftarrow\!\subseteq}\;
{\bf Semigrp}\; \overset{E_1}{\leftarrow\!\subseteq}\;
{\bf Set}
%`$

増強の定義域も書くと次のようです。

$`\quad {\bf Mon} \overset{E_2}{\leftarrow} \cat{I}_2 \subseteq
{\bf Semigrp} \overset{E_1}{\leftarrow} \cat{I}_1 \subseteq
{\bf Set}
%`$

型クラスの名前は次のように解釈します。

後で定義される予定の増強 $`E_1`$ を、名前 Semigroup で呼ぶ。
後で定義される予定の増強 $`E_2`$ または増強の繰り返し $`E_1 * E_2`$ を、名前 Monoid で呼ぶ。

実際の増強の定義は型インスタンス達の定義になります。“増強＝型インスタンスの集まり”を人が個別具体的に定義するなら、次のようになります。

$`\cat{I}_1, \cat{I}_2`$ は有限離散圏となる。つまり、$`\cat{I}_1, \cat{I}_2`$ は、対象集合の有限部分集合。
$`E_2`$ は、$`E_1`$ の像集合 $`E_1(\cat{I}_1) \subseteq |{\bf Semigrp}|`$ の部分集合上で定義されている。つまり、$`\cat{I}_2 \subseteq E_1(\cat{I}_1)`$ 。

有限集合の包含関係により、以下のことが説明できます。

圏論的には、忘却関手 $`{\bf Mon} \overset{U_2}{\to} {\bf Semigrp} \overset{U_1}{\to} {\bf Set}`$ があっても、

$`{\bf Mon} \subseteq {\bf Semigrp}`$
$`{\bf Semigrp} \subseteq {\bf Set}`$

とは全然言えない！

型クラスベースで考えると、

モノイド（Monoid の型インスタンス）は半群〈Semigroup の型インスタンス〉の特殊なもの〈special case〉だ
半群は集合〈プレーンな型〉の特殊なものだ

と言ったりする。

$`E_2(\cat{I}_2) \cong \cat{I}_2,\, \cat{I}_2 \subseteq E_1(\cat{I}_1),\, E_1(\cat{I}_1) \cong \cat{I}_1`$ を考慮すると、

$`E_2(\cat{I}_2) \subseteq E_1(\cat{I}_1) `$ （定義済みのモノイドの有限集合が、定義済みの半群の有限集合の部分集合）
$`E_1(\cat{I}_1) \subseteq \cat{I}_0`$ （定義済みの半群の有限集合が、定義済みの集合の有限集合 $`\cat{I}_0`$の部分集合）

のように見えることは納得できる。

納得はできますが、圏論的事実とは異なります。

型インスタンスは、時間とともに増やしていくのが普通なので、増強は“拡張”されます。一般に、忘却関手 $`U:\cat{C} \to \cat{C}`$ に対する2つの増強 $`E, E'`$ があるとき、$`E'`$ が $`E`$ の拡張〈extension〉であるとは：

$`E: \cat{D}\supseteq \cat{I} \to \cat{C}`$ （$`\cat{I}`$ は事実上有限集合）
$`E': \cat{D}\supseteq \cat{I'} \to \cat{C}`$ （$`\cat{I'}`$ も事実上有限集合）
$`\cat{I} \subseteq \cat{I'}`$
$`E'|_{\cat{I}} = E \text{ on } \cat{I}`$

型クラスにより忘却関手（むしろ忘却写像）と増強の枠組みを宣言し、型インスタンスにより実際の増強を定義し、その増強を徐々に拡張していくことが、Haskell風型クラスの運用法です。

抽象的・超越的に定義される構造達の外延（その外延も構造を持つ、例えば圏 $`{\bf Mon}`$）と、具体的に定義済みな構造達の有限集合（上で定義した $`E_2(\cat{I}_2) \subseteq |{\bf Mon}|`$ ）では、メンタルモデルがだいぶ違います。この食い違いがコミュニケーションの障害になることがあります*2。

↑図の説明：忘却関手を射影と考えて（全射的とは限らないが）、ベースから有限個（図では5個の赤い点）を選んでインスタンスとする。ベースのインスタンスの一部（3個の赤い点）からファイバー内の一点を選ぶ写像を作る。この選択関数が増強。増強された $`\cat{C}`$ 内のインスタンス3個は、ベース $`\cat{D}`$ の3個と呼び名がオーバーロードされる。

フリーモナドは自由なのか

この節では、フリーモナドの「自由さ」について詮索してみます。かなり抽象的な話題なので、流し読みでも、なんなら飛ばしてもかまいません。

「自由」と聞くと、自由忘却随伴系〈free-forgetful adjunction〉を思い起こします。自由モノイドや自由ベクトル空間などは、自由忘却随伴系の枠組みで定義されます。フリーモナドの「フリー」がこの意味の自由だとすれば、次のような自由忘却随伴系があるはずです。

$`\quad \mathbb{F}: [{\bf Set}, {\bf Set}] \to {\bf Mnd} \In {\bf CAT}\\
\quad \mathbb{U}: {\bf Mnd} \to [{\bf Set}, {\bf Set}] \In {\bf CAT}\\
\quad \mathbb{F} \dashv \mathbb{U}
%`$

$`\mathbb{U}`$ はモナドにその台関手〈underlying functor〉、モナド準同型射にその台自然変換〈underlying natural transformation〉を対応させる関手です。$`\mathbb{U}`$ の定義はハッキリしてます。もし、集合圏の自己関手から（集合圏上の）モナドを自由生成する関手 $`\mathbb{F}`$ があれば、次のホムセット同型が成立します。

$`\For F \in |[{\bf Set}, {\bf Set}]|, M \in |{\bf Mnd}|\\
\quad {\bf Mnd}(\mathbb{F}(F), M) \cong [{\bf Set}, {\bf Set}](F, \mathbb{U}(M))
%`$

仮に自由忘却随伴系が作れなかったとしても、次の意味の自由モナドは定義できます（nLab項目 free monad 参照）。

特定の関手 $`F \in |[{\bf Set},{\bf Set}]|`$ に対して、忘却関手 $`\mathbb{U}`$ に関する $`F`$ 上の自由対象〈free object〉 $`M`$。
特定のモナド $`M \in |{\bf Mnd}|`$ が、自己関手 $`F`$ の上に代数的自由〈algebraically-free〉であること。

これらの性質を形式的に書いておきます。

$`\For \mathbb{U}: {\bf Mnd} \to [{\bf Set},{\bf Set}] \In {\bf CAT}\\
\For F \in |[{\bf Set},{\bf Set}]|, M \in |{\bf Mnd}|, \eta: F\to \mathbb{U}(M) \In [{\bf Set}, {\bf Set}]\\
\quad \mrm{IsFreeObjectOn}_\mathbb{U}(M, F, \eta) :\Iff \\
\qquad \forall N\in |{\bf Mnd}|. \forall \alpha : F \to \mathbb{U}(N) \In [{\bf Set},{\bf Set}]. \\
\qquad \quad \exists! \beta : M \to N \In {\bf Mnd}.\, \eta ; \mathbb{U}(\beta) = \alpha : F \to \mathbb{U}(N) \In [{\bf Set},{\bf Set}]
%`$

以下で、$`\mrm{EMAlg}(-)`$ はモナドのアイレンベルク／ムーア代数〈有法則代数〉の圏、$`\mrm{LamAlg}(-)`$ は自己関手のランベック代数〈無法則代数〉の圏を表します。$`\overset{\sim}{\equiv}`$ は圏同値を意味します。

$`\For F \in |[{\bf Set},{\bf Set}]|, M \in |{\bf Mnd}|\\
\quad \mrm{IsAlgebraicallyFreeOn}(M, F) :\Iff \\
\qquad \mrm{EMAlg}(M) \overset{\sim}{\equiv} \mrm{LamAlg}(F) \In {\bf CAT}
%`$

$`\mrm{IsFreeObjectOn}_\mathbb{U}`$ の定義では、自己関手圏とモナドの圏を単に圏だとみなして1-圏の記法を使ってますが、実体が関手と自然変換であることに注目して書けば、次のようになります。

$`\quad \mrm{IsFreeObjectOn}_\mathbb{U}(M, F, \eta) :\Iff \\
\qquad \forall N = (N, \mu, \eta) \in |{\bf Mnd}|.\\
\qquad \forall \alpha :: F \twoto \mathbb{U}(N) : {\bf Set} \to {\bf Set} \In {\bf CAT}.\\
\qquad \exists! \beta :: M \twoto N : {\bf Set} \to {\bf Set} \In {\bf CAT}\text{ monad homomorphism }.\\
\qquad \quad \eta * \mathbb{U}(\beta) = \alpha :: F \twoto \mathbb{U}(N) : {\bf Set}\to{\bf Set} \In {\bf CAT}
%`$

以上の定義を鑑みると、フリーモナドの構成・判定の問題は次の3つが考えられます。

忘却関手 $`\mathbb{U}`$ に対する自由生成関手〈左随伴関手〉 $`\mathbb{F}`$ を構成せよ。
与えられた関手〈集合圏の自己関手〉 $`F`$ に対して、忘却関手 $`\mathbb{U}`$ に関する $`F`$ 上の自由対象 $`M`$ を構成せよ。
与えられたモナド $`M`$ が、関手〈集合圏の自己関手〉 $`F`$ の上に代数的自由であるかどうかを判定せよ。

一番目ができればニ番目は解けます。また、すべての $`F`$ に対して、二番目の構成が系統的にできれば一番目が解けます。三番目に関しては、次の結果が知られているようです（nLab項目 free monad 参照）。

モナド $`M`$ は、関手 $`F`$ 上に代数的自由である ⇔ モナド $`M`$ は、忘却関手 $`\mathbb{U}`$ に関して、ある関手 $`F`$ の上の自由対象である

形式的に書けば次のようです。

$`\For \mathbb{U}: {\bf Mnd} \to [{\bf Set},{\bf Set}] \In {\bf CAT}\\
\For F \in |[{\bf Set},{\bf Set}]|, M \in |{\bf Mnd}| \\
\quad \mrm{IsAlgebraicallyFreeOn}(M, F) \Iff \\
\quad \exists \eta: F\to \mathbb{U}(M) \In [{\bf Set}, {\bf Set}]. \mrm{IsFreeObjectOn}_\mathbb{U}(M, F, \eta)
%`$

肝心の一番目の構成ですが、ある種の余極限に対して余連続な〈余極限を保存する〉自己関手に限定すれば、次の自由忘却随伴系が構成できます。

$`\quad \mathbb{F}: [{\bf Set}, {\bf Set}]_\mrm{Good} \to {\bf Mnd}_\mrm{Good} \In {\bf CAT}\\
\quad \mathbb{U}: {\bf Mnd}_\mrm{Good} \to [{\bf Set}, {\bf Set}]_\mrm{Good} \In {\bf CAT}\\
\quad \mathbb{F} \dashv \mathbb{U}
%`$

下付きの $`{_\mrm{Good}}`$ は、タチの良いモノ達の集まりであることを示します。応用上よく現れる自己関手、例えば多項式関手はタチの良い自己関手です。

フリーモナドはツリーモナド

前節で、タチの良い自己関手 $`F\in|[{\bf Set}, {\bf Set}]_\mrm{Good}|`$ に対してなら、自由忘却随伴系の意味での自由モナド $`\mathbb{F}(F) \in |{\bf Mnd}_\mrm{Good}|`$ が構成できると言いました。（集合圏上の）モナド $`\mathbb{F}(F)`$ とはいったいどんなものなのか？理論的な構成より先に、直感的・具体的な説明をします。

Free と Tree は綴りが似てますが、フリーモナドの実体はツリーモナドです。それを示唆する状況証拠は、以下のデータ型定義です。

data Tree a
  = Leaf a
  | Tree (Tree a) (Tree a)

data Free f a
  = Pure a
  | Free (f (Free f a))

似てますよね。これらのデータ型定義の分析は後回しにして、ツリーモナドに親しむことにします。上の Tree はニ分木〈binary tree〉の定義です。まずはニ分木から始めましょう。

ニ分木のモナドは、記号の乱用で次のように書けます。
$`\quad \mrm{BinTree} = (\mrm{BinTree}, \mu, \eta)\;\in |{\bf Mnd}|`$
モナドの台関手である $`\mrm{BinTree}`$ はおおよそ次のように記述できます。

$`|{\bf Set}|\ni X \mapsto \mrm{BinTree}(X)`$ は、末端〈リーフノード〉に集合 $`X`$ の要素をラベルしたすべての二分木からなる集合
$`(f:X \to Y \In {\bf Set}) \mapsto (\mrm{BinTree}(f):\mrm{BinTree}(X) \to \mrm{BinTree}(Y))`$ は、二分木の末端〈リーフノード〉のラベルを、関数 $`f`$ により書き換える〈リラベリングする〉写像

ラベルの集合を $`X = {\bf Z}`$ とした場合の二分木を幾つか描いてみます。

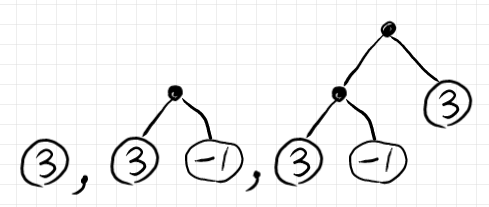
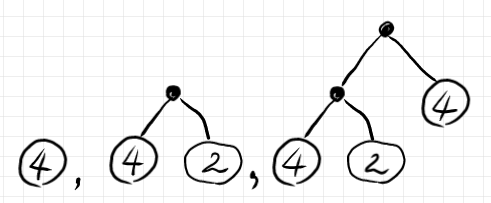
整数でラベルされたリーフノードだけでも（特殊な）二分木とみなします。二分木の左右の高さ（深さ?）が不揃いでもかまいません。これらの二分木を
$`\quad f: {\bf Z}\ni n \mapsto |n| + 1 \in {\bf N}`$
でリラベリングすると次のようになります。

リーフノードやブランチングノード（リーフ以外のノード）にタグ〈札〉を付けると次のようになります。

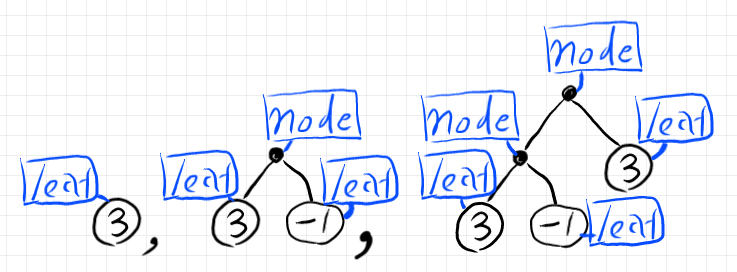
タグ付きの二分木データは次のように書き表すことにします。

$`\text{@leaf }3`$
$`\text{@node }(\text{@leaf }3, \text{@leaf }-1)`$
$`\text{@node}(\text{@node }(\text{@leaf }3, \text{@leaf }-1), \text{@leaf }3)`$

タグを前提にすると、モナドの単位や乗法の記述が分かりやすくなります。

$`\eta_X = \mrm{single}_X : X \to \mrm{BinTree}(X) \In {\bf Set}\\
\For x\in X\\
\quad \mrm{single}_X(x) := \text{@leaf }x\\
\:\\
\mu_X = \mrm{flatten}_X : \mrm{BinTree}(\mrm{BinTrer}(X)) \to \mrm{BinTrer}(X) \In {\bf Set}\\
\For t\in \mrm{BinTree}(\mrm{BinTrer}(X))\\
\quad \mrm{flatten}_X(t) := \\
\qquad \text{case t of }\\
\qquad \quad t = \text{@leaf }s \text{ where }s \in \mrm{BinTree}(X)\\
\qquad\quad \Imp s\\
\qquad \quad t = \text{@node }(s, s') \text{ where }(s, s') \in (\mrm{BinTrer}(\mrm{BinTrer}(X)))^2\\
\qquad \quad \Imp \text{@node }(\mrm{flatten}_X(s), \mrm{flatten}_X(s'))\\
\qquad \text{end}
`$

二分木の場合、親ノード〈ブランチングノード〉の子供達〈children〉は、左右二本のサブツリーです。逆に、二分木のペアから、ルートノードを付け足して二分木を構築〈make〉できます。この構築関数を $`\tau = \mrm{makeTree}`$ とします。

$`\tau_X = \mrm{makeTree}_X : \mrm{Sq}(\mrm{BinTree}(X)) \to \mrm{BinTree}(X) \In {\bf Set}`$

ここで、$`\mrm{Sq}`$ は、集合／写像を二乗〈平方 | square〉する関手です。$`\mrm{Pair}`$ は集合／写像の掛け算とします。

$`\quad \mrm{Sq}(y) := \mrm{Pair}(y, y) = y \times y = y^2`$

二分木構築関数 $`\mrm{makeTree}_X`$ は次のように定義されます。

$`\tau_X = \mrm{makeTree}_X : \mrm{Sq}(\mrm{BinTree}(X)) \to \mrm{BinTree}(X) \In {\bf Set}\\
\For p = (t, t') \in \mrm{Sq}(\mrm{BinTree}(X))\\
\quad \mrm{makeTree}_X(p) = \mrm{makeTree}_X( (t, t')) := \text{@node }(t, t')
`$

$`\mrm{makeTree}_X`$ を使って $`\mrm{flatten}_X`$ を書き直すと次のようです。

$`\mu_X = \mrm{flatten}_X : \mrm{BinTree}(\mrm{BinTrer}(X)) \to \mrm{BinTrer}(X) \In {\bf Set}\\
\For t\in \mrm{BinTree}(\mrm{BinTrer}(X))\\
\quad \mrm{flatten}_X(t) := \\
\qquad \text{case t of }\\
\qquad \quad t = \text{@leaf }s \text{ where }s \in \mrm{BinTree}(X)\\
\qquad\quad \Imp s\\
\qquad \quad t = \text{@node }(s, s') \text{ where }(s, s') \in \mrm{Sq}(\mrm{BinTrer}(\mrm{BinTrer}(X)) )\\
\qquad \quad \Imp \mrm{makeTree}_X( (\mrm{flatten}_X(s), \mrm{flatten}_X(s') ) )\\
\qquad \text{end}
`$

もっとツリーモナド

二分木以外のツリーモナドも考えてみます。親ノード〈ブランチングノード〉は任意の数の子供ノードを持てて、兄弟のあいだに順序（長幼）がある場合を考えます。このようなツリーを順序木〈ordered tree〉といいます（正確には、sibling-ordered tree）。

順序木のモナドは、記号の乱用で次のように書きます。
$`\quad \mrm{OrdTree} = (\mrm{OrdTree}, \mu, \eta) \in |{\bf Mnd}|`$
モナドの台関手である $`\mrm{OrdTree}`$ はおおよそ次のように記述できます。

$`|{\bf Set}|\ni X \mapsto \mrm{OrdTree}(X)`$ は、末端〈リーフノード〉に集合 $`X`$ の要素をラベルしたすべての順序木からなる集合
$`(f:X \to Y \In {\bf Set}) \mapsto (\mrm{OrdTree}(f):\mrm{OrdTree}(X) \to \mrm{OrdTree}(Y))`$ は、順序木の末端〈リーフノード〉のラベルを、関数 $`f`$ により書き換える〈リラベリングする〉写像

順序木も二分木の場合と同じように、タグを使って書き表します。リストは $`[a_1, \cdots, a_n]`$ の形で書きます。$`\mrm{OrdTree}({\bf Z})`$ の要素を幾つか挙げます。

$`\text{@leaf }3`$
$`\text{@node } [\text{@leaf }3, \text{@leaf }-1]`$
$`\text{@node } [\text{@leaf }3, \text{@leaf }-1, \text{@leaf }3]`$
$`\text{@node } [\,]`$
$`\text{@node } [\text{@leaf }3]`$
$`\text{@node} [ \text{@leaf }3, \text{@node }[ \text{@leaf }3, \text{@node }[\,] ] ]`$

ちょっとウザいので $`\text{@leaf}`$ タグは省略すると：

$`3`$
$`\text{@node } [3, -1]`$
$`\text{@node } [3, -1, 3]`$
$`\text{@node } [\,]`$
$`\text{@node } [3]`$
$`\text{@node} [ 3, \text{@node }[ 3, \text{@node }[\,] ] ]`$

単なる整数リーフノード $`\text{@leaf }3`$（または $`3`$）と $`\text{@node } [\text{@leaf }3]`$（または $`\text{@node } [3]`$）は別物として扱います。

順序木モナドの単位と乗法を定義しておきます。単位・乗法となる総称関数の名前は二分木の場合と同じ（オーバーロードする）とします。$`\mrm{List}_\mrm{mor}(-)`$ はリスト関手の射パート〈morphism part〉です。$`\mrm{fmap}_{\mrm{List}}(-)`$ とか $`\mrm{List}.\mrm{fmap}(-)`$ とか書いたほうが落ち着く人は心のなかで書き換えてください。圏論記法に慣れている人なら単なる $`\mrm{List}(-)`$ のほうが好きかも知れません。

$`\eta_X = \mrm{single}_X : X \to \mrm{OrdTree}(X) \In {\bf Set}\\
\For x\in X\\
\quad \mrm{single}_X(x) := \text{@leaf }x\\
\:\\
\mu_X = \mrm{flatten}_X : \mrm{OrdTree}(\mrm{OrdTrer}(X)) \to \mrm{OrdTrer}(X) \In {\bf Set}\\
\For t\in \mrm{OrdTree}(\mrm{OrdTrer}(X))\\
\quad \mrm{flatten}_X(t) := \\
\qquad \text{case t of }\\
\qquad \quad t = \text{@leaf }s \text{ where }s \in \mrm{OrdTree}(X)\\
\qquad \quad \Imp s\\
\qquad \quad t = \text{@node } l \text{ where }l \in \mrm{List}(\mrm{OrdTree}(\mrm{OrdTree}(X)) )\\
\qquad \quad \Imp \text{@node }( \mrm{List}_\mrm{mor}(\mrm{flatten}_X)(l) )\\
\qquad \text{end}
`$

順序木のリストにルートノードを付け足して順序ツリーを構築する関数 $`\tau = \mrm{makeTree}`$ も定義しましょう。

$`\tau_X = \mrm{makeTree}_X : \mrm{List}(\mrm{OrdTree}(X)) \to \mrm{OrdTree}(X) \In {\bf Set}\\
\For l \in \mrm{List}(\mrm{OrdTree}(X))\\
\quad \mrm{makeTree}_X(l) := \text{@node } l
`$

二分木のときと同じですね。この調子で、兄弟ノードのあいだに順序がないようなツリーである無順序木〈unorderd tree〉のモナド $`\mrm{UnordTree}`$ も定義してみてください。子供達のコレクションはバッグ〈bag | マルチセット | multiset〉となるので、素材にバッグ関手を使います。

もうお分かりでしょう。コレクションデータ型を作る関手（モナドである必要はない） $`\mrm{Sq}, \mrm{List}, \mrm{Bag}`$ などは、親ノード〈ブランチングノード〉の子供達のコレクションを作るために利用されています。子供達のコレクション〈collection of children〉を作る関手 $`F`$ があれば、それをもとにしたツリーモナド $`\mrm{Tree}_F`$ を構成できるのです。

$`\mrm{BinTree} = \mrm{Tree}_\mrm{Sq}`$
$`\mrm{OrdTree} = \mrm{Tree}_\mrm{List}`$
$`\mrm{UnordTree} = \mrm{Tree}_\mrm{Bag}`$

一般に、$`\mrm{Tree}_F`$ の単位と乗法は次のように定義されます。

$`\eta_X = \mrm{single}_X : X \to \mrm{Tree}_F(X) \In {\bf Set}\\
\For x\in X\\
\quad \mrm{single}_X(x) := \text{@leaf }x\\
\:\\
\mu_X = \mrm{flatten}_X : \mrm{Tree}_F(\mrm{Trer}_F(X)) \to \mrm{Trer}_F(X) \In {\bf Set}\\
\For t\in \mrm{Tree}_F(\mrm{Trer}_F(X))\\
\quad \mrm{flatten}_X(t) := \\
\qquad \text{case t of }\\
\qquad \quad t = \text{@leaf } s \text{ where }s \in \mrm{Tree}_F(X)\\
\qquad \quad \Imp s\\
\qquad \quad t = \text{@node } c \text{ where }c \in F(\mrm{Tree}_F(\mrm{Tree}_F(X)) )\\
\qquad \quad \Imp \text{@node }( F_\mrm{mor}(\mrm{flatten}_X)(c) )\\
\qquad \text{end}
`$

ツリーのコレクションにルートノードを付け足してツリーを構築する関数は：

$`\tau_X = \mrm{makeTree}_X : F(\mrm{Tree}_F(X)) \to \mrm{Tree}_F(X) \In {\bf Set}\\
\For c \in F(\mrm{Tree}_F(X))\\
\quad \mrm{makeTree}_X(c) := \text{@node } c
`$

帰納的な生成規則

$`F`$-コレクションが子供達であるようなツリーデータの全体が $`\mrm{Tree}_F(X)`$ です。引数となる集合 $`X`$ はリーフノードに割り当てるラベルの集合です。集合 $`\mrm{Tree}_F(X)`$ は、構文的生成規則〈文法規則〉によっても記述できます。

BNF記法で生成規則を書いてみましょう（BNFに関しては「コンピュータによる言語処理の常識 // レキシング／パージングの実例」参照）。

Tree ::= @leaf X
Tree ::= @node F(Tree)

この生成規則は、帰納的な構成規則として読むことができます。

ベース： $`X`$ の要素にタグ $`\text{@leaf}`$ と付けたものはツリーである。
ステップ：既に在るツリー（の集合）から$`F`$-コレクションを作り、そのコレクションにタグ $`\text{@node}`$ を付けたものはまたツリーである。

単一の規則にまとめると次のようです。

Tree ::= @leaf X | @node F(Tree)

集合の帰納的な構成規則として書けば：

$`\mrm{Tree}_F(X) ::= \text{@leaf }X \cup \text{@node }F(\mrm{Tree}_F(X))
%`$

タグ付きユニオンは直和ですから、実は次のように書いても同じです。

$`\mrm{Tree}_F(X) ::= X + F(\mrm{Tree}_F(X))
%`$

Haskell風の構文にするなら次のようです。

data Tree f x
  = Leaf x
  | Node (f (Tree f x))

Tree を Free にして、なぜか（良い習慣だとは思えないが）タグ〈値構成子〉の名前を型構成子名と被らせると、ポピュラーな次の定義が得られます。

data Free f a
  = Pure a
  | Free (f (Free f a))

帰納的な構成規則の不動点方程式としての解釈と、不動点方程式を逐次近似法で解く話は「2」でします。

*1:モナドの圏には色々な定義があります。今回の定義は一番簡単なものです。より一般的定義については「モナド論をヒントに圏論をする（弱2-圏の割と詳しい説明付き） // 左斜め加群と右斜め加群」、「弱2-圏内のモナドに関する補足：モナドが作る2-圏の多様性」参照。また、「モナドはモノイド」に拘らないほうがいいことは「モナドはモノイドだが、モノイドじゃない」に書いてあります。

*2:忘却関手を埋め込みだと誤解している人がいて、話が噛み合わないことがあります。忘却関手のファイバー（一点での逆像）は巨大な集まりになることもあるので、埋め込みからはかけ離れています。