このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

リストモナドとテンソル空間モナドのあいだの準同型射

雑記／備忘

異なる圏の上で定義された2つのモナドを比較したいことがあります。その目的に使える、“異なる圏上のモナドをつなぐ準同型射”は定義されています。そのようなモナド準同型射は一種類ではなくて、色々な定義があります。ここでは、一番扱いやすいと思われる、代数的モナド準同型射（クリメン／ソリヴェレスによる呼び名）の事例を出します。

集合圏Set上のリストモナドと、ベクトル空間の圏VectK上のテンソル空間モナドのあいだの、おそらくは一番素直な準同型射を構成します。

内容

動機と背景

モナドの形式論〈formal theory of monads〉を使うと、次の圏同値は比較的簡単に示せます。

  • 1MndAlg(K) \stackrel{\sim}{=} 1MndEM-Alg(K)
  • 1MndAlg(K) \stackrel{\sim}{=} (1MndKl-Alg(K))op

このことは、「最近のモナド論の概観と注意事項 1/2 // 参考文献と著者」で紹介した"クリメン／ソリヴェレス 2010"に書いてあります。

この圏同値に関わる具体例を提示するのがこの記事の動機／目的です。今日は、上記の圏同値自体は話題にしません。しかし、この記事の記号法が、"クリメン／ソリヴェレス 2010"と同じ記号法ではないので、現状僕が使っている記号の意味だけ簡単にメモしておきます。以下の箇条書きのなかで強調表示されている用語は「随伴に関する注意事項」で説明しています。Kは厳密2-圏だとします。

  • 1AdjL(K) ： Kの対象を対象として、K内の随伴系〈adjunction | adjoint system〉を射とする1-圏。随伴系の左関手の方向を、1AdjL(K)の射（随伴系）の方向とする。左下の'1'は1-圏であることを示し、右下の'L'は左関手の方向を使うことを意味する。
  • MndOn(K)[A] ： A∈|K| として、A上のモナド〈monad on A〉を対象として、モナドのあいだの代数的準同型射〈algebraic homomorphism〉を射とする圏。代数的準同型射とは、モナドをモノイドとみなしてのモノイド準同型射のこと。
  • MndOn(K)[-] ： 1AdjL(K) をインデックス付けベース圏〈indexing category〉とするインデックス付き圏〈indexed category〉。対象Aに対する値はMndOn(K)[A]で、AからBへの随伴により誘導される関手 MndOn(K)[B]→MndOn(K)[A] をリインデキシング関手とする。
  • Flatten(MndOn(K)[-]) ： インデックス付き圏MndOn(K)[-]のグロタンディーク平坦化〈グロタンディーク構成〉。
  • 1MndAlg(K) ： K内のモナドとそのあいだの代数的準同型射からなる圏。1MndAlg(K) := Flatten(MndOn(K)[-]) と定義する。
  • 1MndEM(K) ： K内のモナドとそのあいだのアイレンベルク／ムーア型の準同型射からなる1-圏。アイレンベルク／ムーア型の準同型射については、"クリメン／ソリヴェレス 2010"参照。
  • 1MndKl(K) ： K内のモナドとそのあいだのクライスリ型の準同型射からなる1-圏。クライスリ型の準同型射については、"クリメン／ソリヴェレス 2010"参照。
  • 1MndEM-Alg(K) ： 1MndEM(K)の部分圏で、モナドの準同型射の台関手が右可随伴である（台関手が随伴系の左関手になる）準同型射だけからなる圏。
  • 1MndKl-Alg(K) ： 1MndKl(K)の部分圏で、モナドの準同型射の台関手が左可随伴である（台関手が随伴系の右関手になる）準同型射だけからなる圏。

二番目の圏同値 1MndAlg(K) \stackrel{\sim}{=} (1MndKl-Alg(K))op の右辺が反対圏になってますが、定義の仕方によっては、右肩のopは不要です。MndやAdjでは、誰が見ても明らかな射の方向はないので、射の方向は完全に恣意的（まったく無根拠に決める）ことになります。よって、opが付く／付かないも最初の（恣意的な）定義に依存します。定義の仕方は、著者／論文ごとにバラバラです。

厳密2-圏KとしてCATを選びます。CATは、必ずしも小さくない圏の2-圏です。Set∈|CAT| なので、Set上のモナドも扱えます。以下で扱う事例とは、1MndAlg(CAT) = Flatten(MndOn(CAT)[-]) の典型的な射をひとつだけ取り出して説明します。それは、Set上のリストモナドと、VectK上のテンソル空間モナドのあいだのモナド準同型射です。

リストモナドとテンソル空間モナド

モナドを表すのに、記号の乱用をして M = (M, η, μ) のように書きます。文字'M'をモナドとその台関手の両方の意味でオーバーロード〈多義的使用〉します。別なモナドNでも、単位ηと乗法μは同じ文字を使って N = (N, η, μ) と書きます。紛らわしいときは、N = (N, ηN, μN) とします。モナドが乗っている圏を明示したいときは、M = (M, η, μ) on C とします。台圏Cまで明示すれば、次のことが分かります。

  • M:C→C in CAT
  • η::IdC⇒M:C→C in CAT
  • μ::M*M⇒M:C→C in CAT （'*'は関手の図式順結合）

リストモナド List = (List, η, μ) on Set は、最も有名なモナドと言っていいでしょう。リストモナドは、自由-忘却スタイルの随伴対に分解〈factorize〉できます。Monをモノイドの圏として：

  • 自由モノイド生成関手 FreeMon:Set→Mon in CAT
  • 台集合をとる忘却関手 U:Mon→Set in CAT

これらは随伴系 (η, ε: FreeMon -| U, FreeMon:Set→Mon) を構成します（随伴系の書き方については、「随伴に関する注意事項 // 随伴系の方向」参照）。Listは List = FreeMon*U と書けます。ここで、'*'は図式順の関手結合です。

Kを体として、K上のベクトル空間の圏をVectKとします。そして、K上の多元環の圏をAlgKとします。「多元環」とは、"algebra"に対する古い訳語で、いまどき「多元環」を使う人も少ないでしょうが、僕は「代数」より「多元環」をよく使います*1。VectKとAlgKのあいだの次の関手を考えます。

  • 自由多元環生成関手 FreeAlg:VectK→AlgK in CAT
  • 台ベクトル空間をとる忘却関手 U:AlgK→VectK in CAT

忘却関手を表す文字Uはオーバーロードしています。これらは随伴系 (η, ε: FreeAlg -| U, FreeAlg:VectK→AlgK) を構成します。FreeAlg*U:VectK→VectK はモナドの台関手になります。

V∈|VectK| に対して、FreeAlg(V)は、Vのテンソル多元環〈tensor algebra〉とも呼ばれます。U(FreeAlg(V))は、テンソル多元環の掛け算を忘れたベクトル空間になるので、Vのテンソル空間と呼びましょう。Tens = FreeAlg*U と置いて、Tens = (Tens, η, μ) on VectK はモナドになります。このモナドを、テンソル空間モナド〈tensor-space monad〉と呼びます。

Set上のリストモナドListと、VectK上のテンソル空間モナドTensは、作り方も雰囲気も似てます。無関係とは考えにくいですね。リストモナドとテンソル空間モナドを結ぶモナドの準同型射があって然るべきでしょう。

モナドを随伴系に沿って引き戻す

リストモナドListはSet上にあり、テンソル空間モナドTensはVectK上にあります。台となる圏が違っています。このため、異なる台圏を結ぶ算段が必要になります。

ところで、同じ台圏上のモナドのあいだの準同型射はどう定義されるのでしょうか。色々な定義があり得ますが、一番簡単なのは、モノイド準同型射として定義することでしょう。モノイド準同型射は、モノイドの単位と乗法〈積〉写像を保存する写像です。同様に、モナドの単位自然変換と乗法自然変換を保存する自然変換として、モナド間の準同型射を定義します。

2つのモナド (M, η, μ), (N, η, μ) on C に対して、自然変換 φ::M⇒N:C→C が次の等式条件（の絵）を満たすときに、φはモナド準同型射です。

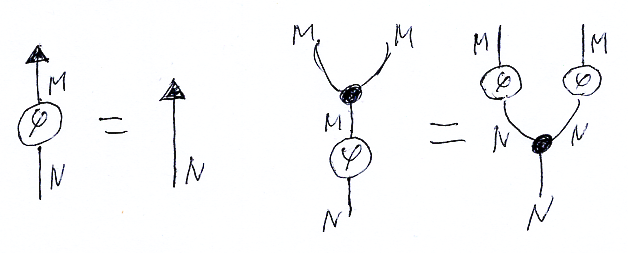
ここで、黒三角がη、黒丸がμです。

例えば、Maybe = (Maybe, η, μ) on Set から List = (List, η, μ) on Set へのモナド準同型として、自然変換φを次のように定義してみます。

  • For A in Set, φA:Myabe(A)→List(A) in Set,
    φA(a) := [a] if a∈A,
    φA(⊥) := []

ここで、[a] はシングルトンリスト、⊥はMaybeで追加した要素、[] は空リストです。φの自然性はすぐに示せるので、φはモナドMaybeをモナドListに埋め込む準同型射になります。このことは次のように書けます。

  • φ:Maybe→List in MndOn(CAT)[Set]

MndOn(CAT)[Set] は、CAT内でSet上に居るモナド達からなる圏です。

テンソル空間モナドはSet上に居ないので、Set上に“移動”させます。移動の手段として、SetとVectKのあいだの随伴系を使います。SetとVectKのあいだには、典型的な自由-忘却スタイルの随伴系があります。それは：

  • (η, ε: FreeVect -| U, FreeVect:Set→VectK)

ここで、文字'η'がモナドの単位とオーバーロードされていて、文字'U'も毎回オーバーロードですが、文脈で区別してください。

一般論として、随伴系 (η, ε: F -| U, F:C→D) があると、D上のモナド N = (N, η, μ) on D をC上に移動（引き戻し）できます。移動後のモナドを N' = (N', η', μ') on C とすると：

  • N' := F*N*U :C→C
  • η' := η;(F*ηN*U) ::IdC⇒N':C→C
  • μ' := (F*N*ε*N*U);(F*μ*U) ::N'*N'⇒N':C→C

ここで、ηは随伴系の単位で、ηNはモナドの単位です。'*'は関手の図式順結合および関手と自然変換のヒゲ結合で、';'は自然変換の図式順縦結合です。η'とμ'を絵（ストリング図）で描けば：

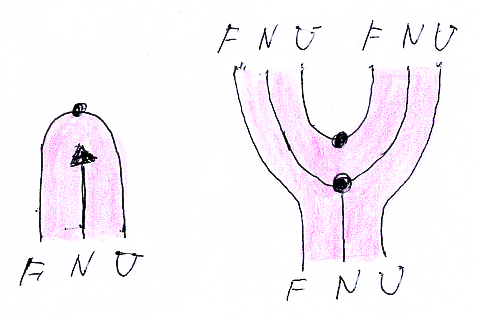
絵において、黒三角はモナドのηNで、黒丸は随伴のη, εとモナドのμです。圏D（を表す領域）をピンクに塗っています。

N' = (N', η', μ') on C が結合律と左単位律、右単位律を満たすことは絵算を使えば簡単に示せます。

VectK上のモナド Tens = (Tens, η, μ) をSet上に移動（引き戻し）する場合は：

  • Tens' := FreeVect*Tens*U:Set→Set
  • η' := η;(FreeVect*ηTens*U)::IdSet⇒Tens':Set→Set
  • μ' := (FreeVect*Tens*ε*Tens*U);(FreeVect*μ*U)::Tens'*Tens'⇒Tens':Set→Set

Tens' = (Tens', η', μ') はSet上のモナドであり、もとのTensのSet上の代理となります。

リストモナドからテンソル空間モナドへの準同型射

リストモナドListからテンソル空間モナドTensへの準同型射は、次のように定義します； まず、Tensの代理としてのTens'をSet上に構成し、Set上の準同型 φ:List→Tens' in MndOn(CAT)[Set] を List→Tens の準同型射とします。φは、次の絵のような感じです。圏VectKを表す領域はピンクに塗ってあります。

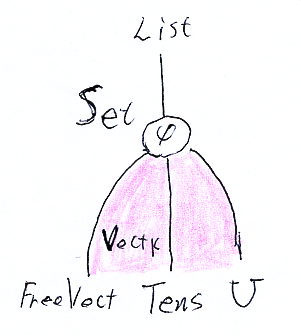
集合Aに対して、自然変換φのA-成分は。

  • φA:List(A)→U(Tens(FreeVect(A)))

となります。U(Tens(FreeVect(A))) をもう少しわかりやすく記述しましょう。U(Tens(FreeVect(A))) は、なんだかんだで（詳細割愛）、集合Aの要素を不定元とするK係数非可換多項式全体の集合になります。K係数非可換多項式全体の集合を NCPolyK(A) とすれば、

  • U(Tens(FreeVect(A))) \stackrel{\sim}{=} NCPolyK(A)

この同型はイコールとみなしてしまっていいでしょう。

a = [a1, ..., an] ∈ List(A) とすると、φA(a) は次のように与えられます。

  • φA:List(A)→NCPolyK(A) in Set
  • φA(a) := a1 ... an （すべて並べる）
  • φA([]) := 1

a1 ... an はリストの要素をすべて並べて掛け合わせた単項式で、NCPolyK(A) の要素とみなします。

このように定義したφが、Set上のモナド準同型射となるのは、φがモノイド準同型射で、単位と乗法を保つときです。絵で描けば：

これらを確認するのは、定義を追いかけるルーチンな作業です。ルーチンとは言え、具体的な計算はなかなか面倒なので、別な記事にするかも知れません。


冒頭で述べたように、モノイドの形式論からは、かなり抽象度の高い定理が得られます。具体的な感触を得るために実例が欲しいわけですが、その具体的の構成もけっこうめんどくさかったりします。今回の実例は、1MndAlg(CAT) 内の射をひとつだけ構成したのでした。その射が φ:(List on Set)→(Tens on VectK) in 1MndAlg(CAT) です。

φの周辺には、Set, Mon, VectK, AlgK という4つの圏（CATおよび1AdjL(CAT)の対象）があり、それらは随伴系（1AdjL(CAT)の射）で結ばれています。この四角形（対角線付き）は、事例としてなかなか面白いと思います。

*1:"algebra"はすべて「多元環」にするわけじゃないです。例えば、"Boolean algebra"は「ブール多元環」じゃなくて「ブール代数」です。