多相関数と依存型をちゃんと理解しよう - 檜山正幸のキマイラ飼育記 (はてなBlog)

比較的最近（今年の9月）、多相関数の記事を書きました。「多相関数」「総称関数」という言葉は知っていても、理解があやふやな人もいそうです。基本的なところを復習しましょう。話を明確にするために、少し圏論を使います。

[さらに追記]下の追記における「間違いです」が間違いだったようです。用語法の流儀が複数あるので、どっちも許容でした。追記内の表は、2つの用語法の対照表になります。[/さらに追記]

[追記]
~~この記事内で使っている言葉「依存積型」と「依存和型」は間違いです。申し訳ありません。正しい呼び名は次のとおりです。~~

記号	~~間違った~~ 呼び方 1	~~正しい~~ 呼び方 2	別な呼び方
$\prod$	依存積型	依存指数型／依存関数型	パイ型
$\sum$	依存和型	依存積型	シグマ型

「依存型と総称型の圏論的解釈」の冒頭で~~釈明(?)~~説明を書いています。

間違いも記録として残しておく方針なので、お手数ですが、本文内の「依存積型」を「依存指数型」、「依存和型」を「依存積型」に置換して読んでください。
[/追記]

内容：

多相関数のプロファイル
型と関数の圏
型ファミリー
依存型：依存積型と依存和型
依存和型：型ファミリーの総和
依存和型もっと
依存積型：型ファミリーの総積
依存積型もっと
多相関数の表現方法
おわりに

多相関数のプロファイル

「蒸し返し：アドホック多相 vs パラメトリック多相」では、多相関数lengthを例題にしました。lengthのプロファイル（入力と出力の仕様）を次のように書きました。

$length :: \forall\alpha. \mathrm{List}\, \alpha \to Int$

この書き方はHaskell風なので、クセの無い書き方なら：

$length : \forall\alpha. \mathrm{List}(\alpha) \to Int$

コロンは1個で、適用（引数渡し）は丸括弧を使いました。' $\forall$ 'は論理の全称記号ですが、単に記号を借用しているだけです*1。誤解と混乱を避けるためには、いったんは全称記号とのアナロジーを断ち切ったほうが無難です。依存型と述語論理の関係は、いずれ書く機会があるでしょう、たぶん。

上記のプロファイルでは「ギリシャ文字小文字は型を表す」約束ですが、一般的な“パラメータを持った型”を扱いたいので、多相関数のプロファイル記述は次の形にします。

$f : \forall x \in X. F(x) \to G(x)$

ここで：

fは多相関数（ちゃんとした定義は後述）
Xはパラメータの集合（集合なら何でもいい）
xは何らかのパラメータ（xは束縛変数になる）
F(x) と G(x) はパラメータを持った型

パラメータ a∈X を固定すると、通常の型〈集合〉のあいだの通常の関数〈写像〉になります。

$f_a : F(a) \to G(a)$

lengthの例では、G(x) がxによらずにいつでも Int だったわけです。その意味でlengthは特殊な例なので、別な例を挙げましょう。「ツリーデータ型のモナド」で紹介したリーフ値付きツリー〈leaf valued tree〉LVTree_K(A) を思い出してください。LVTree_K(A) の部分集合を定義しましょう。

LVOTree(A) ⊆ LVTree_N(A)

部分集合 LVOTree(A) が何であるか説明します； LVTree_N(A) は、キー（グラフの辺ラベル、パスのセグメント）の集合をNとしたリーフ値付きツリーの集合です。Nを単なる可算無限集合と捉えるのではなく、通常の大小順序で全順序集合と考えます。兄弟ノード達を、0 < 1 < 2 < ... と連番で番号付けます。すると、兄弟のあいだに順序が決まります；長男ノード、次男ノード、‥‥ という具合に。このような番号付けと兄弟間全順序を持つリーフ値付きツリーの集合が LVOTree(A) です。LVOは、Leaf Velued and Ordered です。下図は兄弟間の順序と、ノードのパス表現（赤字、スラッシュと数字1が紛らわしいかな）を示した図です。

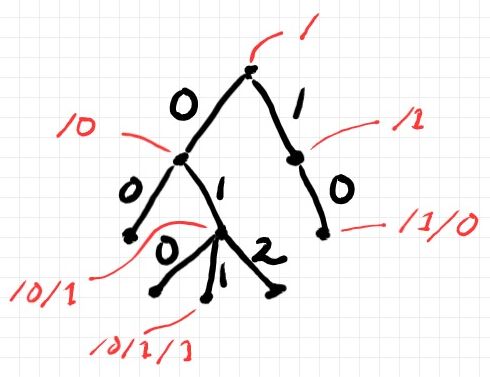
t∈LVOTree(A) に対して、兄弟間の順序と親子関係を組み合わせることにより、深さ優先探索の順序として、tのノードの集合にも全順序が決まります。tのノード達は一列に並べることができるのです。

t∈LVOTree(A) に対して、リーフ（端点）の値を順に拾って並べるとリストができます。できたリストを leaves(t) とします。多相関数 leaves のプロファイルは次のように書けます。

$leaves : \forall\alpha\in \mathrm{Type}. \mathrm{LVOTree}(\alpha) \to \mathrm{List}(\alpha)$

ここで出てきたTypeについては次節で説明します。

型と関数の圏

型や関数の話をするときには、舞台となる圏をセットアップします。圏論にあまり馴染みがない方は、この節は流し読みでかまいません。

型を対象として、関数を射とする圏をCとします。Cを、完全に抽象的な圏だとすると話がややこしくなるので、集合圏Setの部分圏だとします。単なる部分圏ではやりたいことが出来ないので、次の条件を付けます。

Cは、集合圏の直積と指数を引き継いてデカルト閉圏になる。

言い方を換えると、Cはデカルト閉圏Setの部分デカルト閉圏です。これは、C内で集合の直積 A×B、集合の指数 B^A = [A, B] = (AからBへのすべての関数の集合) が自由に使えることです。

他に、極限・余極限に関して（デカルト閉圏より強い）条件が必要になることがありますが、必要になったら言及することにします。圏のサイズの問題を回避するためにCは小さい圏〈small category〉だと仮定することもあります。要するに、都合のいい条件を適宜付け加えて考える、ってことです。しかし、Cを完全に具体化すると窮屈過ぎるので、完全な具体化はしません。

さて、Type := |C| と定義します。Cの対象である集合を「型」と呼ぶので、これは当たり前の定義です。C が小さい圏なら、Type = |C| は集合になります。集合と型を同義で使うので、この場合は「Typeも型〈集合〉だ」は正しいです。が、Type∈Type はウソです。

Typeは型だ。
Typeは型の集合だ。
よって、型Typeは、型の集合Typeの要素だ。

という、インチキな推論をしているのです。こういう“字面だけのマヤカシ”を真に受けてはダメですよ*2。

Cが小さくないとき -- 極端なケースとして C = Set のときなど -- は、Type∈|Set| になりません。じゃ、どうするか？おそらく、グロタンディーク宇宙を引き合いに出さないといけないので、この話はやめます。心の安らぎを得たい人は、Cは小さいと仮定してください。

Typeは“今考え得るすべての型の集合”なので、Typeの部分集合は素朴な意味で“型の型”になります。“型の型”を表す安定した用語はありませんが、ここでは型カインド〈type kind〉と呼んでおきます。

Kが型カインドである ⇔ K⊆Type ⇔ K⊆|C|

仮にCが大きな圏でも、考える型カインドを小さいものに限れば、サイズの問題は回避できます。サイズの大小をいちいちチェックしたくないので、ここではそういう制約は採用しませんけど（ものぐさ）。

型ファミリー

最初の節で「パラメータを持った型」という言葉を出しました。「パラメータ」より「インデックス」と呼ぶほうが多いかも知れません。「インデックスを持った型」ですね。言い回しとしては、

インデックス付き型
インデックスされた型

のほうが語感がいいかも。英語でフルに書けば indexed family of types なので、直訳なら「インデックスされた型の族」です。‥‥ てなことを考えると、言葉はやたら増えます。正規表現（「用語のバリエーション記述のための正規表現」参照）で書けば：

{{インデックス | パラメータ}{付き | された}}?型{の}?{族 | ファミリー}?

どれで呼ぼうが全部同義です。ここでは型ファミリー〈type family〉を選んでおきます。

型値関数〈type-valued function〉が一番素直な言い方だと思います。残念ながら、型値関数はあまり使われない言葉です。

型ファミリーは F:X → Type という関数に過ぎませんが、行きがかり上、関数の域〈domain〉をインデキシング集合〈indexing set〉と呼びます。これは行きがかり上なので、いつもどおり域と言う（言ってしまう）ことがあるかも知れません。

型ファミリー〈型値関数〉のインデキシング集合〈域〉が型カインド〈型の集合〉のとき、世間では総称型と呼んでるんじゃないのかな。実際のところ、合意された正確な定義があるわけでもないので（コミュニティごとのジャーゴンがあるだけなので）何とも言えませんが、ここでは、インデキシング集合が型カインドである型ファミリーが総称型〈generic type〉だとします。

型から型を作るのが総称型なら、それは型構成子と同じでは？特別なニュアンスを込めないなら、総称型と型構成子は同義です。それと、多相型も同義です、たぶん。なんでこんなに同義語が溢れかえっているの？ワシャ知らん！*3

依存型：依存積型と依存和型

再び、多相関数のプロファイルの話に戻ります。

$f : \forall x \in X. F(x) \to G(x)$

この書き方は使います（特に忌避しません）が、「蒸し返し：アドホック多相 vs パラメトリック多相」で次のように書いてます。

僕は、ここに'∀'を使うのは好きではありません、だって論理の'∀'とあんまり似てないもんね。まー、意味ではなくて単に記号だけテキトーに借用していると解釈しましょう。

好きではないのです。じゃ、どんな書き方が好きかというと、次の形です。

$f \in \prod_{ x \in X} [F(x), G(x)]$

または、

$f:\sum_{x \in X}F(x) \to \sum_{x \in X}G(x) \mbox{ over } X$

ここで、 $\prod_{ x \in X}$ は総積の記号、 $\sum_{x \in X}$ は総和の記号です。型に関して使われたときは、依存積〈dependent product〉と依存和〈dependent sum〉を表します（定義は後述）。下付きや特殊なフォントが使えないときは通常テキストで次のように書きます。

f∈(Πx∈X.[F(x), G(x)])
f:Σx∈X.F(x) → Σx∈X.G(x) over X

多相関数をちゃんと定義する／ちゃんと理解するとは、多相関数のプロファイルの意味をハッキリさせることに他なりません。多相関数のプロファイルのなかに依存積や依存和が登場しているので、依存積・依存和の意味をハッキリさせることも必要です。

集合と関数〈写像〉の概念を組み合わせて、依存積・依存和と多相関数をちゃんと定義できます。圏論を知っていれば手っ取り早い定義も可能です（すぐ下の補足）。が、この記事の残りの部分では、集合と写像を手でいじくり回して、依存型と多相関数を説明します。

[補足]
集合Xを離散圏とみなします。離散圏も同じ記号Xで表します。すると、型ファミリー F, G:X → |C| は関手となるので、F, G:X → C in CAT です。したがって、F, G∈|[X, C]| と書けます。ここで、[-, -] は関手圏を表します。fは関手圏 [X, C] の射、つまり自然変換とします。

f:F → G in [X, C]
f∈[X, C](F, G)
f::F ⇒ G:F → G in CAT

上の3つの書き方はどれも同値です。この状況のとき、fは型ファミリーFから型ファミリーGへの多相関数です。（定義、終わり。）

Cが集合圏の部分デカルト閉圏ならば、指数 [-, -] があります。ブラケット記号が関手圏とオーバーロードされてますが、今度のブラケットはCの指数です。H(x) := [F(x), G(x)] と定義される H:X → C も関手になります。Cが十分な極限を持つとして、A := Lim H と定義します。Aは極限錐の頂点集合です。この集合Aが、依存積型 Πx∈X.[F(x), G(x)] と同じものです。

集合Aの要素、あるいは写像 1 → A in C と、FからGへの自然変換は1：1に対応します。この対応により、F ⇒ G:X → C という自然変換と Πx∈X.[F(x), G(x)] の要素を同一視すると、次の書き方になります。

f∈(Πx∈X.[F(x), G(x)])
f:Σx∈X.F(x) → Σx∈X.G(x) over X

下のほうのプロファイルは、自然変換の成分 f_x:F(x) → G(x) が寄せ集まった様子を記述しています。ここで出てきた依存和型 Σx∈X.F(x)、Σx∈X.G(x) は余極限として定義できます。

これで、多相関数のプロファイルの2つの書き方を合理化できました。以上が、圏論を使った依存型と多相関数の定義（の概略）です。
[/補足]

依存和型：型ファミリーの総和

それでは、依存和型を具体的に地道に作っていきましょう。依存和型は（依存積型もだけど）型ファミリーに対して定義されます。F:X → Type を型ファミリーとします。念のため再度確認しておくと、Type = |C| で、Cは集合圏の部分圏でした。x∈X に対して値 F(x) は型、つまり集合なので、次の合併集合が作れます。

$\mathscr{F} := \bigcup_{x\in X} F(x)$

$\mathscr{F}$ は合併集合なので次が成立します。

$a\in \mathscr{F} \Leftrightarrow \exists t \in X.( a\in F(t))$

型ファミリーFの依存和型〈dependent sum type | 総和集合〉は次のように定義します。

$\sum_{x\in X}F(x) := \{(x, y) \in X\times \mathscr{F} \mid y \in F(x) \}$

これだけだとピンと来ないかも知れないので、X = {1, 2} のときを考えてみましょう。

$\mathscr{F} := \bigcup_{x\in \{1, 2\}} F(x) = F(1)\cup F(2)$

これより、

$a\in \mathscr{F} \Leftrightarrow \exists t \in \{1, 2\}.( a\in F(t)) \Leftrightarrow a\in F(1) \lor a\in F(2)$

X = {1, 2} の場合の依存和型の定義は：

$\sum_{x\in \{1, 2\}}F(x) := \{(x, y) \in \{1, 2\}\times \mathscr{F} \mid y \in F(x) \}$

書き換えると：

$\:\:\:\: \{(x, y) \in \{1, 2\}\times \mathscr{F} \mid y \in F(x) \} \\ = \{(x, y) \in \{1, 2\}\times (F(1)\cup F(2)) \mid y \in F(x) \} \\ = \{(1, y) \in \{1\}\times (F(1)\cup F(2)) \mid y \in F(1) \} \cup \\ \:\:\:\: \{(2, y) \in \{2\}\times (F(1)\cup F(2)) \mid y \in F(2) \} \\ = (\{1\}\times F(1)) \cup (\{2\}\times F(2))$

さらに、 $A := F(1),\; B := F(2)$ と置けば、最後に得られた集合は：

$(\{1\}\times A) \cup (\{2\}\times B) = A + B$

集合の直和 A + B はこのように定義されるのでした（下図も参照）。

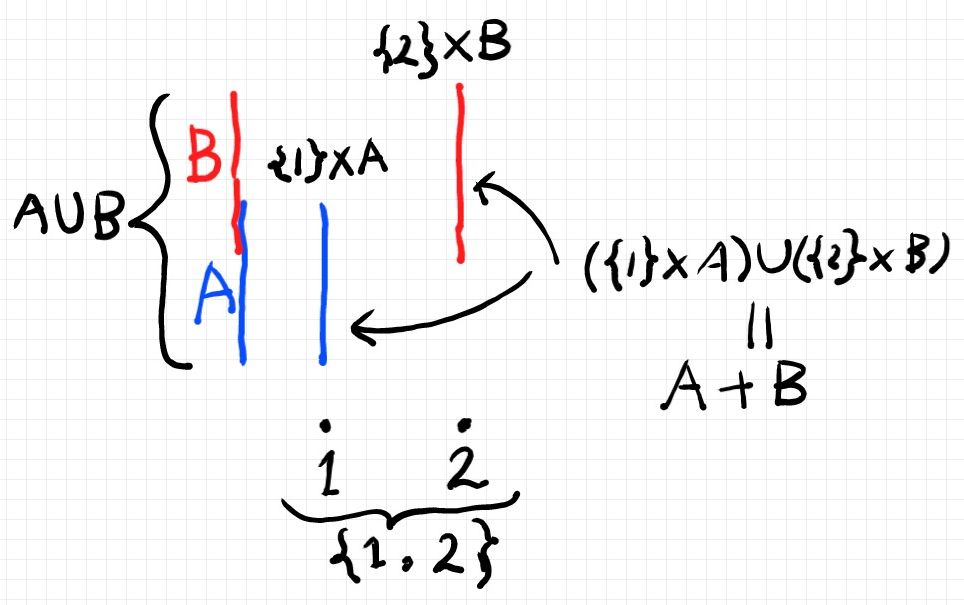
依存和型もっと

型ファミリー〈型値関数〉 F:X → Type に対する依存和型 Σx∈X.F(x) は、直感的に言えば、集合 F(x) 達を互いに共通部分がないように“引き離して”寄せ集めたものです。寄せ集めることが足し算に似ているので、総和記号を使って書きます。

依存和型〈総和集合〉構成のときに問題となるのは、どうやって「共通部分がないように引き離す」かです。引き離す算段として、x∈X ごとに {x}×F(x) を作って、それらを寄せ集めています。

$\sum_{x\in X}F(x) = \bigcup_{x\in X}(\{x\}\times F(x))$

前節の定義では、 $\bigcup_{x\in X}(\{x\}\times F(x) )$ を、 $X \times (\bigcup_{x\in X}F(x) )$ の部分集合とみなしています。

$\sum_{x\in X}F(x) \subseteq X \times (\bigcup_{x\in X}F(x) )$

こう考えると、依存和型の要素は、 $(x, y),\; x\in X,\; y\in \bigcup_{x\in X}F(x)$ の形をしています。ただし、 $x\in F(x)$ の条件は満たしています。

直積集合 $X \times (\bigcup_{x\in X}F(x) )$ の第一射影を π、第二射影を β とします。πとβを $\sum_{x\in X}F(x)$ に制限すると、次の図式になります。

$\require{AMScd} \begin{CD} \sum_{x\in X}F(x) @>{\beta^F}>> \bigcup_{x\in X}F(x) \\ @V{\pi^F}VV \\ X \end{CD}$

πとβの右肩にFを付けているのは、Fごとにπとβは異なるからです。が、通常は右肩のFは省略します。

総和と合併を型ファミリー〈型値関数〉に対するオペレーターと考えれば、次のように簡潔に書けます。

$\require{AMScd} \begin{CD} \sum(F) @>{\beta^F}>> \bigcup(F) \\ @V{\pi^F}VV \\ \mathrm{dom}(F) \end{CD}$

Fのインデキシング集合〈Fの域〉が有限集合のときは、Fの依存和型を弁別子付きユニオン型〈descriminated union type〉と言います（「ユニオン」の代わりに「バリアント」ということもあります）。dom(F) = (Fのインデキシング集合) の要素を弁別子〈descriminator〉とかタイプタグ〈type tag〉あるいは単にタグ〈tag〉と呼びます。

ここでは、X = dom(F) が有限でも有限でなくても何であっても、Xの要素をタグと呼びます。そして、型ファミリー〈型値関数〉Fの依存和型〈総和集合〉Σ(F)の要素をタグ付き値〈tagged value〉と呼びます。z∈Σ(F) に対して、

π(z) は、タグ付き値zのタグ
β(z) は、タグ付き値zのボディ〈body〉

「タグとボディ」は、以前Kuwataさんと僕が作っていたスクリプト言語で使っていた用語です。そのスクリプト言語では、タグ付き値（タグとボディのペア）(x, y) を @x y と書いていました。この記事では逆順の y@x と書くことにします（理由は後述）。y@x は (x, y) と同じですが、アットマークにより依存和型の要素であることを強調・明示します。

タグ付き値の処理には、タグ部分でパターンマッチ＆分岐するケース文が使えます。X = {1, 2} で、F(1) = A, F(2) = B であれば、Σ(F) = A + B として：

case z∈(A + B) of
  a@1 => (a∈A に対する処理)
or
  b@2 => (b∈A に対する処理)
endcase

型そのものがタグになっている場合は、型ケース文になります*4。X = {Int, String} で、F(Int) = Int, F(String) = String であれば、Σ(F) = Int + String として：

case z∈(Int + String) of
  i@Int => (i∈Int に対する処理)
or
  s@String => (s∈String に対する処理)
endcase

型そのものがタグになっている場合は、i@Int = (Int, i) は、「型 Int に所属する i」の意味です。型が特定済みのデータですね。この場合だと、アットマークを使った「i@Int ＝型 Int に所属する i」はメールアドレスみたいな印象がありませんか？*5（これが、記法の由来。）

実在するプログラミング言語における依存和型〈ユニオン型〉の話が次の記事にあります。

TypeScriptのはなし：ユニオン型がけっこうイイね

依存和型をケンロニストがどう捉えるかは下の補足に書いときます。

[補足]
先の補足に書いたように、型ファミリーを離散圏からの関手 F:X → C in CAT とみなすと、Fの余極限として依存和型を定義できます。が、別の捉え方もあります。

C⊆Set であり、Setの対象である集合は離散圏とみなせ、写像は離散圏のあいだの関手とみなせるので、Set⊆Cat です。結局、C → Cat と埋め込めるので、型ファミリー（離散圏からの関手） F:X → C は F:X → Cat とみなすことができます。

以上のように考えれば、型ファミリーFは、離散圏Xから“圏の圏”Catへの関手です。これは、Xをインデキシング圏とするインデックス付き圏〈indexed category〉です。インデックス付き圏については次の記事参照。

インデックス付き圏のグロタンディーク構成

インデックス付き圏 F:X → Cat にグロタンディーク構成を施して得られた平坦化圏が依存和型に対応します。射影 π^F:Σ(F) → X はグロタンディーク構成のファイブレーションです。
[/補足]

依存積型：型ファミリーの総積

依存積型を具体的に定義するとき、（僕が）思いつく方法が2つあります。どっちを採用してもできる集合は同型なので、抽象レベルでは「どっちでも同じ、どうでもいい」のですが、具体的な計算・処理だと差が出るので、どっちにするか悩みます。悩んだ結果、Map(X, ∪(F)) の部分集合として定義する方法をプライマリにします。別な方法も（セカンダリとして）後で紹介します。

記号の約束：圏Cのホムセット C(A, B) を Map_C(A, B) とも書きます。Cは集合圏の部分圏だったので、ホムセットは写像〈関数〉の集合ですから、Cに属する写像〈map〉を Map_C と書くのはいいでしょう。さらに、Cを前提にしている状況では、Map_C(A, B) = Map(A, B) と略記します。

C(A, B) = Map_C(A, B) = Map(A, B) （今の文脈では）
f:A → B in C ⇔ f∈Map(A, B) （今の文脈では）

依存和型と同様、依存積型も型ファミリー F:X → Type に対して定義されます。型ファミリーFに対する依存積型は次のように書きます（書き方だけ）。

$\prod_{x\in X}F(x) = \prod(F) = \Pi(F)$

型ファミリーFから依存積型を作る操作をオペレーターと考えれば、Xやxは不要です（Xは dom(F) として得られる）。TeXだと、総積記号と大文字パイは違う記号ですが、どっちでもいいです。

予告どおり、Fの依存積型〈dependent prduct type〉 Π(F) を、Map(X, ∪(F)) の部分集合として定義します。

$\prod(F) := \{t\in Map(X, \bigcup(F) ) \mid \forall x\in X.(\, t(x) \in F(x) \,)\}$

定義から当然に $\prod(F) \subseteq Map(X, \bigcup(F) )$ です。したがって、依存積型の要素は、 $t:X → \bigcup(F)$ という写像です。ただし、tが勝手な写像でいいわけではなくて、xに対する値 t(x) は型ファミリーの値 F(x) に入っている必要があります。

依存和型のときと同様に、X = {1, 2} , F(1) = A, F(2) = B として考えてみましょう。このとき、∪(F) = A∪B なので、Π(F) ⊆ Map({1, 2}, A∪B) です。t∈Π(F) である条件は：

∀x∈{1, 2}.( t(1)∈A かつ t(2)∈B)

t = (t(1), t(2)) と書くなら、tは直積 A×B の要素とみなせます。なので、次の同型が成立します。

Π(F) $\cong$ A×B

これで、インデキシング集合が {1, 2} の型ファミリーFの依存積型は F(1)×F(2) と同型だと分かりました。言い方を換えれば、依存積型は直積型の一般化です。この事情から、依存積型の要素をタプル〈tuple〉と呼びます。タプル（実体は関数）tの値 t(x) をタプルtの成分〈component〉と呼びます。「タプルと成分」に対する同義語は山ほどありますが、めんどくさいので列挙はしません。

t∈Π(F) のとき、型ファミリーFはタプルtの型スキーマ（データベースで言えばテーブルスキーマ）だと言えます。今は、データベースの用語「スキーマ」を使ったのですが、型理論としては誰かが「型スキーマ」に別な意味を与えているかも知れません（「型理論ってば」参照）。

依存積型もっと

具体的な計算を行う場合などは、依存和型と依存積型を関連付けておいたほうが便利です。なので、以下では依存和型を使って依存積型を定義します。

型ファミリー F:X → Type に対する依存積型を Π(F) と書きましたが（前節のプライマリな定義で）、依存和型も Σ(F) と簡潔に書くことにします。

$\Sigma(F) := \sum_{x\in X}F(x)$

Σ(F) は簡潔ですが、情報が欠損するような省略ではありません。インデキシング集合Xは、dom(F)として回復できますし、束縛変数xはもともと無意味な記号です。

π:Σ(F) → X は、π(y@x) = π((x, y)) = x として定義されて、射影〈projection〉とも呼びます。射影はタグ（ペアの第1成分）を取り出す写像です。なお、タプルの成分を取る写像 s $\mapsto$ s(x) も射影と呼びます。こういう用語の衝突は避けられないので諦めて注意しましょう。

さて、型ファミリー F:X → Type から作った射影 π:Σ(F) → X に対して、写像〈関数〉 s:X → Σ(F) が、

s;π = id_X （π $\circ$ s = id_X）

を満たすとき、セクション〈section〉または選択関数〈choice function〉と呼びます。

射影 π:Σ(F) → X に対するセクションの全体を Γ(π:Σ(F) → X) と書きセクション集合〈section set〉と呼びます。射影π（正確にはπ^F）は型ファミリーの依存和型から自動的に決まるので、セクション集合を Γ(Σ(F)) と略記します。

今定義したセクション集合 Γ(Σ(F)) = Γ(π:Σ(F) → X) が依存積型の第二の定義です。第二の定義は Π' という記号で表すとして：

Π'(F) := Γ(Σ(F))

(Fの依存積型) = (Fの依存和型のセクション集合) です。Π'(F) = Γ(Σ(F)) をもうちょいゴチャゴチャと書けば：

${\prod'}_{x\in X}F(x) = \Gamma( \sum_{x\in X}F(x) )$

依存積型の第二の定義（今定義したばっかり）と第一の定義（前節）の関係を考えましょう。次の図式（簡略化したよ）を思い出してください。

$\require{AMScd} \begin{CD} \Sigma(F) @>{\beta}>> \cup(F) \\ @V{\pi}VV \\ X \end{CD}$

セクション s:X → Σ(F) に対して、βを後結合〈post-compose〉した (s;β):X → U(F) は、(s;β)∈Map(X, ∪(F)) ですが、(s;β)∈Π(F) となります。βを後結合する写像〈βによる前送り〉を β_* とすると、β_* が Π'(F) と Π(F) の同型を与えます（細部は各自確認してみてください）。

$\beta_\ast:\Gamma(\Sigma(F)) \to Map(X, \cup(F) )$
$s \in \Gamma(\Sigma(F)) \Leftrightarrow \beta_\ast(s) \in \Pi(F) \subseteq Map(X, \cup(F))$
$\Pi'(F) = \Gamma(\Sigma(F)) \cong \Pi(F)$

Π(F) と Π'(F) は集合として同型なので同一視可能です。が、現実レベル／具体レベルでは区別したほうがいいでしょう。事例を挙げます。

X = {"name", "age"} として、型ファミリーFを F("name") = String, F("age") = Int とします。Fの依存積型 Π(F) の要素〈タプル〉tを次のように定めます。

t("name") := "坂東トン吉" ∈String
t("age") := 25 ∈Int

このタプル t∈Π(F) に対応するセクションを s∈Π'(F) （Π'(F) = Γ(Σ(F)）とします。つまり、β_*(s) = t です。s:X → Σ(F) は次のようになります。

s("name") := "坂東トン吉"@"name" ∈({"name"}×String)
s("age") := 25@"age" ∈({"age"}×Int)

関数sの値に、引数をタグとしてエンコードしています。冗長な印象ですが、このような関数sは関数値の集合だけで表現できます。

s = {"坂東トン吉"@"name", 25@"age"}

あるいは、JSON構文で書くなら：

s = {"name" : "坂東トン吉", "age" : 25}

「型ファミリー、依存和型、依存積型」という3つの概念で説明が付くことが、コミュニティごとのジャーゴン〈方言〉が多数あるので、複雑で錯綜した印象を与えてしまっています。

多相関数の表現方法

冒頭で、多相関数のプロファイル記述を2種類挙げました。

$f \in \prod_{ x \in X} [F(x), G(x)]$
$f:\sum_{x \in X}F(x) \to \sum_{x \in X}G(x) \mbox{ over } X$

ここで、FとGは型ファミリー F:X → Type, G:X → Type です。つまり、インデックス〈パラメータ〉 x∈X ごとに型〈集合〉 F(x) と G(x) が決まります。インデキシング集合〈インデックスの集合〉Xは何でもかまいません。Xが型カインド（e.g. X = Type）でも、X = {1, 2} でも X = N でも、X = {"name", "age"} でも、好きにして。

集合の指数 [A, B] は、AからBへの関数の全体なので、[A, B] = Map(A, B) = C(A, B) です。

さて、最初の記述 $f \in \prod_{ x \in X} [F(x), G(x)]$ を解釈しましょう。依存積型の（一番目の）定義から、

$f:X \to \bigcup_{x\in X}[F(x), G(x)]$
$f(x) \in [F(x), G(x)]$

習慣により、f(x) より f_x, f<x>, f[x] などと書かれるので、fに関する条件は次のように書き換えましょう。

$f_x \in Map(F(x), G(x))$

これは、インデックス（あるいはパラメータ、‥‥(略)）xごとに関数 f_x が与えられているということです。多相関数とは、確かにそういうものです。そう考えれば、 $f \in \prod_{ x \in X} [F(x), G(x)]$ は当たり前のことを言っているだけです。

もうひとつの書き方を見ましょう。

$f:\sum_{x \in X}F(x) \to \sum_{x \in X}G(x) \mbox{ over } X$

お尻についている "over X" がミソです。fは、単に Σ(F) から Σ(G) への関数ではありません。条件がつくのです。その条件とは次の図式を可換にすることです。

$\require{AMScd} \begin{CD} \Sigma(F) @>{f}>> \Sigma(G) \\ @V{\pi^F}VV @VV{\pi^G}V \\ X @= X \end{CD}$

集合Xの要素xについて考えると：

$\require{AMScd} \begin{CD} \{x\}\times F(x) @>{f_x}>> \{x\}\times G(x) \\ @V{ {\pi^F}_x}VV @VV{{\pi^G}_x}V \\ \{x\} @= \{x\} \end{CD}$

ここで出てきた f_x はタグの存在を無視すれば、 $f_x \in Map(F(x), G(x))$ の f_x と同じです。

いずれにしても、xごとの f_x:F(x) → G(x) の寄せ集めが多相関数〈polymorphic function〉だと言っているのです。

[追記]ここで定義した多相関数は、「多相関数と型クラス // 多相関数＝関手間部分変換」の多相関数とは少し違います。それについては、「多相関数：補遺」に書きました。[/追記]

おわりに

以上で次の4つの概念を説明しました。

型ファミリー
依存和型
依存積型
多相関数

型ファミリーに対して、その依存和型と依存積型が定義できました。多相関数は、関数のタプル（指数型の型ファミリーの依存積型の要素）として表すことができます。あるいは、2つの型ファミリーの依存和型のあいだの関数で "over X" の条件を満たすものです。

無意味に細かく分類しないで、少数の概念から構成される俯瞰的構造を理解しておきましょう。

*1:多相関数のプロファイル記述の状況が、Propositions-As-Types解釈において論理の全称記号に対応するのは事実です。が、その対応は直感的に明らかなものではありません。

*2:型の世界Typeに、“万能な型”Uがあって、世界であるTypeがUに吸い込まれるような再起的構造を持つことはあります。それは“字面だけのマヤカシ”ではありません。

*3:ほんとの事情は分かりませんが、おそらく、色々なコミュニティが異なる言葉を使い、誰も集約しようとしないせいでしょう。

*4:我々が作っていたスクリプト言語では、明示的にタグが付いてなくても「暗黙のタグ」が付く仕様でした。例えば、文字列リテラル "hello" は文字列型だと分かるので、@string "hello" と同等に扱います。これにより、タグによるケース分岐と型による分岐は一様に扱えます。

*5:僕みたいな年寄りだと、メールアドレスの書式は、個人名@所属組織名だと思っているのですが、今はそうでもないかもな。