記法をどう取り決めるか? どうでもよさそうでも深刻に悩んでしまうのですよね。悩んだ経緯も含めて、現時点での約束ごとを記しておきます。表題に挙げた 米田の「よ」、米田の星、ディラックのブラケット の概念と記法について述べます。$`
\newcommand{\CoEnd}{\underline{\sum} }
\newcommand{\from}{\lt:}
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\op}{\mathrm{op} }
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Holds}{\Keyword{Holds } }%
\newcommand{\Using}{\quad \Keyword{Using } }%
`$
内容:
はじめに
米田テンソル計算では、次のような記法を使って、記述や計算を楽に気持ちよく進められるようにしたいと思っています。
- 古典テンソル計算記法
- 米田の「よ」
- 米田の星
- ディラックのブラケット記法
これらを一緒に使うことは想定されてないので組み合わせると不整合が生じることがあります。うまく折り合いを付けるのはなかなか難しい。
基本とするアナロジーは次の対応です。
| 古典テンソル計算 | 圏論 |
|---|---|
| インデックス集合 | 圏 |
| スカラー半環 | 集合圏 |
| 関数 | 関手 |
| ベクトル | 余前層 |
| コベクトル | 前層 |
| 行列 | プロ関手 |
米田の「よ」と添字
米田の「よ」は、テンソル計算のクロネッカーのデルタに相当するもので非常に重要です。「よ」には上下の添字を付けて使います。添字の付け方はロマンと同様にします。
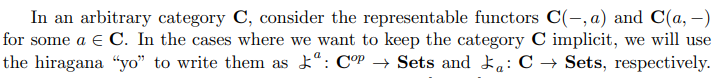
上記の引用は、次の論文のp.19の画像コピーです。
- Title: Profunctor optics and traversals
- Author: Mario Román
- Submitted: 22 Jan 2020
- Pages: 82p
- URL: https://arxiv.org/abs/2001.08045
「よ」の上下添字の意味は次のとおりです。
- $`よ^a = \cat{C}(-, a):\cat{C}^\op \to {\bf Set} `$ 米田埋め込みの値
- $`よ_a = \cat{C}(a, -):\cat{C} \to {\bf Set} `$ 余米田埋め込みの値
$`よ^a`$ は反変関手、$`よ_a`$ は共変関手ですが、$`よ^-`$ は共変関手、$`よ_-`$ は反変関手です。
- $`よ^- :\cat{C} \to [\cat{C}^\op, {\bf Set}] `$ 米田埋め込み
- $`よ_- :\cat{C}^\op \to [\cat{C}, {\bf Set}] `$ 余米田埋め込み
$`よ^-, \, よ_-`$ は関手圏に値を持つ関手です。ここがややこしいので注意が必要です。
ロマン以外でもこの記法は使っているでしょう -- 誰でも思いつきそうですから。しかし、米田の「よ」を普及させたロージエンの教科書の記法とは少し違います。ロージエンの記法では、右下添字に圏を記します。
$`\quad よ_{\cat{C}}: \cat{C} \to [\cat{C}^\op, {\bf Set}] `$ 米田埋め込み
ロマンは、圏 $`\cat{C}`$ は明示的には記述しない方針ですが、明示的に書きたいこともあるので、そのときは左肩に添えることにします。
- $`{^\cat{C}よ}^a = \cat{C}(-, a) `$
- $`{^\cat{C}よ}_a = \cat{C}(a, -) `$
- $`{^\cat{C}よ}^- = \lambda\, x.\, \cat{C}(-, x) `$
- $`{^\cat{C}よ}_- = \lambda\, x.\, \cat{C}(x, -) `$
$`よ = {^\cat{C}よ}`$ は、ホム双関手を表すもので、引数〈argument〉の1つを添字にするとカリー化されます。
- $` よ(a, b) = \cat{C}(a, b)`$
- $` よ_a b = よ_a(b) = よ(a, b) `$
- $` よ^b a = よ^b(a) = よ(a, b) `$
2つの引数の両方を添え字にしてもかまいません。
- $` よ_a^b = {よ_a}^b = よ_a b = よ_a(b) = よ(a, b) `$
- $` よ^b_a = {よ^b}_a = よ^b a = よ^b(a) = よ(a, b) `$
以上の添え字の規則は、古典テンソル計算の習慣と整合します。「米田テンソル計算 2: 準備 // 方向付き区切り記号」で導入した方向付き区切り記号を使うと次のようにも書けます(最後の縦棒は条件付き確率の記法の借用です)。
- $` よ_a^b = よ(a, b) = よ(b \from a) = よ(b \mid a) `$
以下の画像コピーは、先のロマンの論文の“ニンジャ米田の補題〈米田還元〉”の部分です。クロネッカーのデルタ/ディラックのデルタと同様な公式が成立します(「米田の「よ」 ≒ ディラックの「δ」」参照)。積分(コエンド)の密度が上付き添字の「よ」になるのが要注意です。

“ニンジャ米田”に出てくる双対的な概念は:
| 還元 | エンド/コエンド | 密度/余密度 |
|---|---|---|
| 米田還元 | エンド(総積の部分) | 余密度 = 余米田埋め込み |
| 余米田還元 | コエンド(総和の商) | 密度 = 米田埋め込み |
スピヴァックの指数記法
ごく最近、スピヴァックによる次の定義を見つけました。

上記の引用は、次の教科書のp.19の画像コピーです。
- Title: Polynomial Functors: A General Theory of Interaction
- Authors: David I. Spivak, Nelson Niu
- LastUpdated: November 26, 2021
- Pages: 281p
- URL: https://topos.site/poly-book.pdf
スピヴァックは、集合圏に対する余米田埋め込みを $`y^-`$ と書きます。前節の約束とは上下が逆です。文字 y は「米田の y」ですが、特に変わった文字やフォントは使いません。特別な約束として、単に $`y`$ と書くと、それは恒等関手 $` \mathrm{Id}: {\bf Set} \to {\bf Set}`$ のことだとします。
余米田埋め込みに特定の対象を代入した $`y^a`$ は、上付き添字というより指数〈累乗 | ベキ〉なんですね。集合圏の場合は、次のような指数法則が成立します。
- $` y^{a + b} \cong y^a \times y^b `$
- $` y^1 \cong y`$ ($`y = \mathrm{Id}`$)
- $` y^0 \cong 1`$ (1 は単元集合への定数関手)
- $` (y^a)^b \cong y^{a\times b}`$ (カリー同型、やや強引)
- $` (y^a)(b) \cong b^a`$ (イコールだと思ってもよい)
これは自然で気持ちいいですね。同じことを下付き添字の「よ」で書くと:
- $` よ_{a + b} \cong よ_a \times よ_b `$
- うまく書けない
- $` よ_0 \cong 1`$ (1 は単元集合への定数関手)
- うまく書けない
- $` よ_a(b) \cong [a, b]`$ (イコールだと思ってもよい)
あまり気持ちよくないですねー。
スピヴァックのy記法では、文字「y」を予約された不定元とみなせて、集合圏上の自己関手のクラスを、一元〈1変数〉多項式の半環のように捉えることができます。
スピヴァックのy記法が非常に使い勝手がいいので、「よ」の添字の上下を逆転させようかとも思いました。が、そうすると、古典テンソル計算の習慣と相容れないので、米田テンソル計算としては、余米田埋め込みの添字は下付きのまま(スピヴァック記法とは逆)にします。
米田の星と米田埋め込み
米田埋め込み/余米田埋め込みを、「米」を上下に付けて表す記法も我々は使います。
- $`a^{米} := よ^a = \cat{C}(-, a)`$ 米田埋め込みの値
- $`a_{米} := よ_a = \cat{C}(a, -)`$ 余米田埋め込みの値
米田埋め込み/余米田埋め込み自体は次のように書けます。
- $`(-)^{米} := よ^- : \cat{C} \to [\cat{C}^\op, {\bf Set}] `$
- $`(-)_{米} := よ_- :\cat{C}^\op \to [\cat{C}, {\bf Set}] `$
「米」を上下に付ける米田の星記法は、圏の対象/射だけではなく、圏のあいだの関手に対しても使います*1。米田の星(上下の「米」マーク)を付けると、どうなるかは次のように書けます。
$`\For F:\cat{C} \to \cat{D} \In {\bf Cat}\\
\quad F^米 : \cat{D} \to \cat{C} \In {\bf Prof}\\
\quad F_米 : \cat{C} \to \cat{D} \In {\bf Prof}
`$
上付きの星だと反変的対応、下付きの星だと共変的対応という原則は守っています。
関手への米田の星の定義は次のようになります。
$`\For F:\cat{C} \to \cat{D} \In {\bf Cat}\\
\For c \in |\cat{C}|, d\in |\cat{D}|\\
\Define F^米(d, c) := \cat{D}(d, F(c)) \;\in |{\bf Set}|\\
\Define F_米(c, d) := \cat{D}(F(c), d) \;\in |{\bf Set}|\\
\For f:c \to c' \In \cat{C}, g:d \to d' \In \cat{D}\\
\Define F^米(g, f) := \cat{D}(g, F(f)) \;:
\cat{D}(d', F(c)) \to \cat{D}(d, F(c')) \In {\bf Set}\\
\Define F_米(f, g) := \cat{D}(F(f), g) \;:
\cat{D}(F(c'), d) \to \cat{D}(F(c), d') \In {\bf Set}
`$
$`(-)^米`$ が反変的対応であることを示してみましょう。示すべきことは:
$`\For F:\cat{C} \to \cat{D} \In {\bf Prof}\\
\For G:\cat{D} \to \cat{E} \In {\bf Prof}\\
\Holds (F * G)^米 \cong G^米 \diamond F^米 \In {\bf Prof}
`$
ここに出てくる記号は「米田テンソル計算 2: 準備」を見てください。計算は次のようにします。
$`\For c \in |\cat{C}|, e\in |\cat{E}|\\
\quad (G^米 \diamond F^米)(e, c)\\
\Using \diamond \text{の定義}\\
= \CoEnd^{d\in |\cat{D}|} G^米(e, d) \times F^米(d, c)\\
\Using (-)^米 \text{の定義}\\
= \CoEnd^{d\in |\cat{D}|} \cat{E}(e, G(d))\times \cat{D}(d, F(c))\\
\Using \text{よ記法}\\
= \CoEnd^{d\in |\cat{D}|} \cat{E}(e, G(d))\times {^\cat{D}よ}^{F(c)}(d)\\
\Using \text{余米田還元}\\
\cong \cat{E}(e, G(F(c) ) )\\
\Using \text{記法の変更}\\
= \cat{E}(e, (F*G)(c) )\\
\Using (-)^米 \text{の定義}\\
= (F*G)^米 (e, c)
`$
上の計算で、プロ関手のインデックス〈引数〉は対象としていますが、射をインデックスにした場合も同様です。また、$`(-)_米`$ が共変的対応であることも同じく示せます。
圏の対象・射の{余}?米田埋め込みと関手・自然変換の{余}?米田埋め込みの両方に米田の星を使ってますが、これはオーバーロードです。両者はすこし別な対応です。僕は、第一種{余}?米田埋め込み〈type-1 {co}?Yoneda embedding〉/第二種{余}?米田埋め込み〈type-2 {co}?Yoneda embedding〉と区別してますが、それらの関係はまた別な記事で述べます。
ディラックのブラケット記法
ディラックのブラケット記法と線形代数、そして圏論の対応は次のようです。
| ディラック | 線形代数 | 圏論 |
|---|---|---|
| ブラベクトル | コベクトル | 前層 |
| ケットベクトル | ベクトル | 余前層 |
したがって、前層 $`A: \cat{C}^\op \to {\bf Set}`$ はブラケット記法で $`\langle A| `$ と書くことになります。この書き方は、反図式順なら使えるのですが、図式順との相性が悪い! 図式順記法とは相容れないようなので、結局僕はディラックのブラケット記法を全面的に採用するのはあきらめました。
しかしこれは、テキスト記法での使用をあきらめただけで、図式ではブラケットをバリバリ使います。図式におけるブラケット記法、いや、ブラケット図法とは何かというと、前層や余前層を三角形で表すことです。ブラケット記法を図式(絵算)に持ち込んだのはボブ・クックなので、ディラック/クック図法と呼ぶべきかも知れません(米田テンソル計算 1: 経緯と発想 // オックスフォード/ケンブリッジ流の三角・菱形」参照)。
テキストではブラケット記法を使わないと言いましたが、図の情報を写し取る目的には、象形文字としてのブラケット記法を使う可能性はあります。米田の星で表現される前層・余前層は次のように書けます。
$`
\quad a^米 = \langle\![ a |{\scriptstyle \leftarrow} = {\scriptstyle \rightarrow}| a ]\!\rangle \\
\quad a_米 = {\scriptstyle \leftarrow}| a ]\!\rangle = \langle\![ a |{\scriptstyle \rightarrow}
`$
ブラケットに付いている矢印は描画方向を示す矢印です。前層は、右から左ならブラベクトルで、左から右ならケットベクトルで表します。スカラー積としてのホムセットは次のように書けます。
$`
\quad \langle\![ a |{\scriptstyle \rightarrow} \diamond {\scriptstyle \rightarrow}| b ]\!\rangle \cong \cat{C}(a, b) = よ_a^b
\\
\quad \langle\![ b |{\scriptstyle \leftarrow} \odot {\scriptstyle \leftarrow}| a ]\!\rangle \cong \cat{C}(b \from a) = よ_a^b
`$
*1:自然変換に対しても使えます。