互いに逆向きな関手のペア $`F:\mathcal{C} \to \mathcal{D}`$ と $`G:\mathcal{D} \to \mathcal{C}`$ を含むような随伴系〈adjunction | adjoint system〉の定義として、次の2つがよく使われます。
- 自然なホムセット同型
- 単位と余単位を含む代数系
“単位と余単位を含む代数系”から“自然なホムセット同型”を作る作業は、ストリング図と相性がいいので、(ストリング図を使うなら)比較的簡単です。この記事でやってみます。
“自然なホムセット同型”から“単位と余単位を含む代数系”を作るほうは、(僕は)うまくストリング図が描けなくて毎回行き詰まります。なので、やりません(うまくいったら報告するかも)。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\twoto}{\Rightarrow}
\newcommand{\hyp}{\text{-}}
\newcommand{\In}{\text{ in }}
`$
内容:
関連する記事:
代数的な随伴系
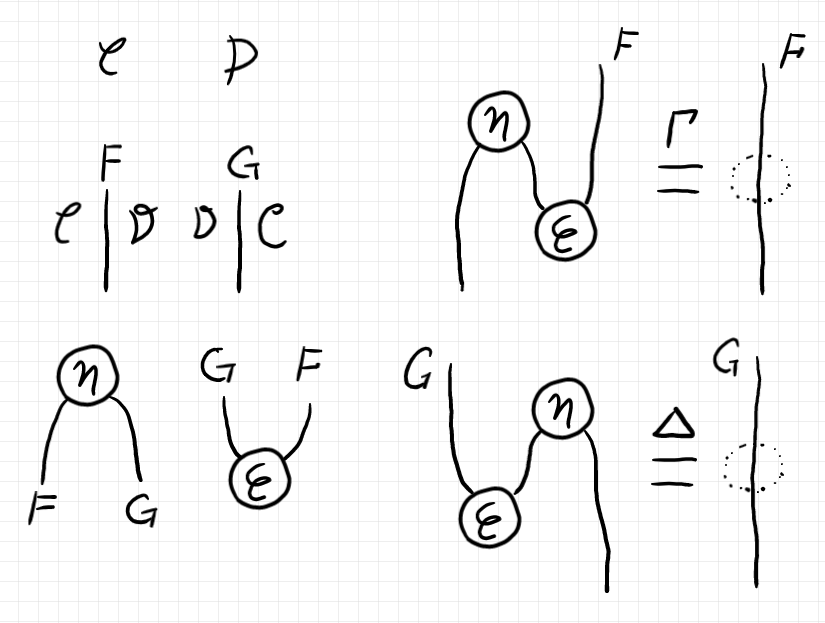
代数的な随伴系(単位と余単位を含む代数系)は、圏の2-圏のなかに実現される等式的な構造で、次の構成素〈constituent〉を持ちます。$`\mrm{Id}_{\hyp}`$ は恒等関手、$`\mrm{ID}_{\hyp}`$ は恒等自然変換です。
- 0次元構成素: 2つの圏 $`\cat{C}, \cat{D}`$
- 1次元構成素: 2つの関手 $`F:\cat{C}\to \cat{D}, G:\cat{D}\to \cat{C}`$
- 2次元構成素: 2つの自然変換 $`\eta:: \mrm{Id}_{\cat{C}} \twoto F*G, \varepsilon :: G*F \twoto \mrm{Id}_{\cat{D}}`$ ($`\eta`$ が単位で、$`\varepsilon`$ が余単位)
- 3次元構成素: 2つの等式 $`\Gamma ::: (\eta * F);(F * \varepsilon) = \mrm{ID}_F, \Delta ::: (G*\eta); (\varepsilon * G) = \mrm{ID}_G`$ (ニョロニョロ関係式〈snake {relation | equation | identity} 〉)
これら一式は、次のような絵〈ストリング図〉に描けます。描画方向は上から下、左から右です。
[追記]
随伴系の2-指標を、色付きのテキスト/ペースティング図/ストリング図で描いたことがあったのを思い出しました。
[/追記]
絵のレイアウトと描画方向(左から右)にあわせるために、演算子記号は図式順を使います(「関手と自然変換の計算に出てくる演算子記号とか // 今後使う予定の演算子記号」参照。)。
絵を使った計算法〈絵算〉の詳しい説明は、「圏論の随伴をちゃんと抑えよう: お絵描き完全解説」にあります。
自然なホムセット同型
$`F, G`$ が随伴ペアを形成しているとき、次のホムセット同型があります。
$`\text{For } X\in |\cat{C}|, Y\in |\cat{D}|\\
\quad \cat{D}(F(X), Y) \cong \cat{C}(X, G(Y)) \In {\bf Set}`$
これが「自然」だとは、集合のあいだの同型が、2つの関手のあいだの自然同型〈natural isomorphism〉として系統的に与えられる、ということです。
自然同型で結ばれる2つの関手を、無名変数 '$`\hyp`$' を使って書くと:
- $`\cat{D}(F(\hyp), \hyp) : \cat{C}^\mrm{op}\times \cat{D} \to {\bf Set}`$
- $`\cat{C}(\hyp, G(\hyp) ) : \cat{C}^\mrm{op}\times \cat{D} \to {\bf Set}`$
自然同型は次のようです。
$`\quad \varphi :: \cat{D}(F(\hyp), \hyp) \twoto \cat{C}(\hyp, G(\hyp) ): \cat{C}^\mrm{op}\times \cat{D} \to {\bf Set}`$
自然性は、次の可換図式で表現されます
$`\require{AMScd}
\text{For }(f, g): (X, Y) \to (X', Y') \In \cat{C}^\mrm{op}\times \cat{D}\\
\begin{CD}
\cat{D}(F(X), Y) @>{\varphi_{X, Y}}>> \cat{C}(X, G(Y) )\\
@V{\cat{D}(F(f), g)}VV @VV{\cat{C}(f, G(g))}V\\
\cat{D}(X', G(Y')) @>{\varphi_{X', Y'}}>> \cat{C}(X', G(Y') )
\end{CD}\\
\text{commutative in }{\bf Set}
`$
等式で書けば:
$`\text{For } u \in \cat{D}(F(X), Y)\\
\quad \varphi_{X', Y'}( \cat{D}(F(f), g)(u) ) = \cat{C}(f, G(g))(\varphi_{X, Y}(u))
`$
ホム関手の射パートは“射のサンドイッチ”で与えられるので:
$`\text{For } u \in \cat{D}(F(X), Y)\\
\quad \varphi_{X', Y'}(g\circ u\circ F(f)) = G(g)\circ \varphi_{X,Y}(u) \circ f
`$
後で使う都合から、図式順記法に直して、$`\varphi`$ はコンビネータ(後述)だと思うと次の形になります。
$`\text{For } u \in \cat{D}(X.F, Y)\\
\quad \varphi_{X', Y'}[ f.F ; u ; g ] = f ; \varphi_{X,Y}[u] ; g.G
`$
単位・余単位の自然性
記法は図式順記法を使います。ドットが適用〈application〉で、セミコロンが縦結合、アスタリスクが横結合です。上下左右が絵と揃います。
随伴系の単位 $`\varepsilon :: \mrm{Id}_\cat{C} \twoto F*G`$ は自然変換です。その自然性は次の図式の可換性で表せます。$`\cat{C}^\mrm{op}`$ を使っているのは他の記述とあわせているだけです。
$`\text{For }f: X\to X' \In \cat{C}^\mrm{op}\; (\text{i.e. }f: X'\to X \In \cat{C} )\\
\begin{CD}
X'.\mrm{Id}_\cat{C} @>{X'.\eta}>> X'.(F*G)\\
@V{f.\mrm{Id}_\cat{C}}VV @VV{f.(F*G)}V\\
X.\mrm{Id}_\cat{C} @>{X.\eta}>> X.(F*G)
\end{CD}\\
\text{commutative in }\cat{C}
`$
等式で書けば:
$`\quad X'.\eta ; f.(F*G) = f.\mrm{Id}_\cat{C} ; X.\eta`$
これを絵の等式として描けば以下のようです。絵の見た目からエレベーター法則とも呼ばれます。
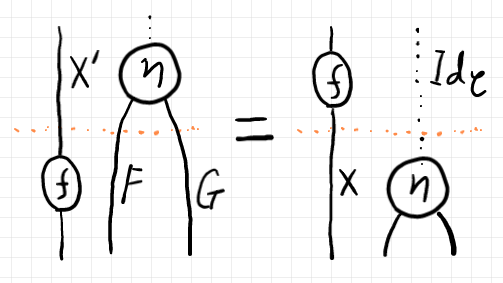
絵のなかで、対象 $`X', X`$ のワイヤーは、自明な圏(対象ひとつ、射ひとつ)からのポインティング関手 $`{X'}^\sim, X^\sim : {\bf 1} \to \cat{C}`$ と同一視しています。そして射 $`f`$ は、自然変換 $`f^\sim :: {X'}^\sim \twoto X^\sim `$ と同一視してます。したがって、$`X', f, X`$ の左の領域は自明な圏 $`{\bf 1}`$ です。
余単位の自然性も同様なエレベーター法則として描画できます。
転置コンビネータと反転置コンビネータ
対象のペア $`X, Y`$ ごとに集合のあいだの写像 $`\varphi_{X, Y}`$ を定義します。
$`\text{For } X\in |\cat{C}|, Y\in |\cat{D}|\\
\quad \varphi_{X, Y} : \cat{D}(F(X), Y) \to \cat{C}(X, G(Y)) \In {\bf Set}`$
これは、自然なホムセット同型になる予定のものですが、とりあえずは単なる写像の族として定義します。
圏の射を渡されて射を返す写像の族を圏論的コンビネータ〈圏論的オペレータ〉と呼びます。随伴のホムセット同型を与える写像を(随伴の)転置写像〈transposition map〉と呼ぶことがあります。なので、$`\varphi_{X, Y}`$ は転置コンビネータ〈transposition combinator〉と呼ぶことにします。
コンビネータ(実体は写像)を、コンビネータ名を右上にマークしたボックスで表します。引数〈argument〉はボックス内に入れます。引数が描き込まれたボックス全体はコンビネータの値〈return value | output〉になります。
コンビネータ $`\varphi`$ は次のような対応になります。
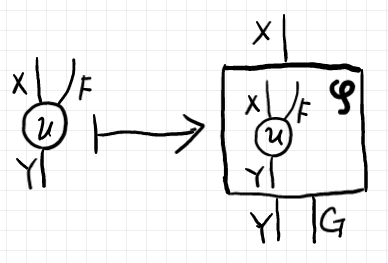
その定義は次のとおり。
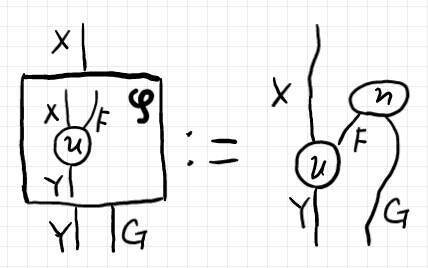
逆向きの反転置コンビネータ〈opposite-transposition combinator〉$`\psi`$ の対応は次のとおり。定義も転置コンビネータと同様で、単位 $`\eta`$ の代わりに余単位 $`\varepsilon`$ を使います。
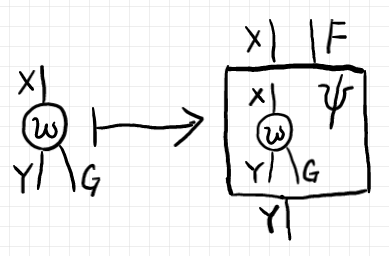
転置コンビネータと反転置コンビネータが互いに逆になることはニョロニョロ関係式(ワイヤー・ストレッチング公式)から分かります。
転置コンビネータの自然性
転置コンビネータ $`\varphi`$ の自然性は、次の等式(再掲)でした。
$`\text{For } u \in \cat{D}(X.F, Y)\\
\quad \varphi_{X', Y'}[ f.F ; u ; g ] = f ; \varphi_{X,Y}[u] ; g.G
`$
これをそのまま絵に描くと次のとおり。
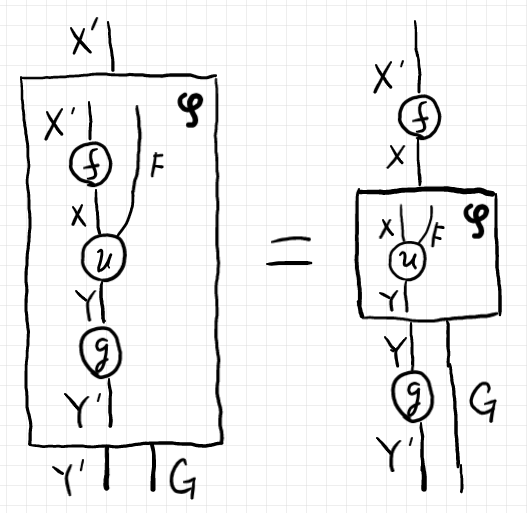
この絵等式〈{graphical | pictorial} equation〉を示せば、転置コンビネータ $`\varphi`$ が自然であると分かります。
転置コンビネータ $`\varphi`$ の定義に現れる単位 $`\eta`$ は自然変換だったので、エレベーター法則で上下にスライドできます。よって、次の絵等式が成立します。
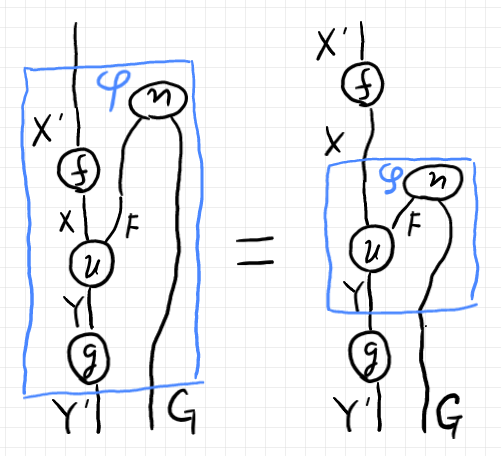
これは、転置コンビネータ $`\varphi`$ の自然性の等式(下に再々掲)そのものです。
$`\quad \varphi_{X', Y'}[ f.F ; u ; g ] = f ; \varphi_{X,Y}[u] ; g.G`$
反転置コンビネータの自然性も同様に示せます。これで、与えられた“代数的随伴系(単位と余単位を含む代数系)”から、自然な転置コンビネータと自然な反転置コンビネータが作れました。つまり、目的の“自然なホムセット同型”が得られました。
[追記 date="2023-07-31"]
先に自然なホムセット同型が与えられて、そこから代数的な随伴系を構成することができるのですが、うまいやり方が見つかりません。身も蓋も無いやり方は次の記事に書きました。
[/追記]