「だいたい圏になる: 概圏」の概圏の事例の記述がグダグダでした。修正を入れましたが、もとの文言をできるだけ残して修正・追記しているので読みにくいかも知れません。整理してもう一度最初から述べます。
概圏の3つの事例を、3つの構成〈construction〉として述べます。
- Span構成: ファイバー積を持つ圏からスパンの概圏を作る構成法
- Env構成: モノイド圏から環境付き射の概圏を作る構成法
- State構成: 対称モノイド圏から状態付き射の概圏を作る構成法
これら3つの構成をできるだけ統一的に記述します。ホムセット上の同値関係は、同型射の作用により記述します。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
\newcommand{\Imp}{ \Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{-} }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Where}{\Keyword{Where } }%
`$
内容:
関連記事:
はじめに
与えられた圏から別な“圏”を作る構成法がこの記事の主題です。最初に与えられる圏は、小さくなくてもいいですが、局所小圏〈locally small category〉だとします。構成された“圏”は、実際は概圏〈almost category〉で局所小だとは限りません。圏の法則も等式的に成立するとは限りません。
概圏のホムセットに載ってる同値関係で商集合を作ると、それらの商集合をホムセットとする概圏は厳密な(法則が等式的に成立する)概圏となります。厳密な概圏は、ホムセットのサイズを気にしなければ圏そのものです。商集合を作る過程で、サイズも小さくなるときがあります。そのとき、得られた概圏は局所小圏になります。
以下のすべての構成において、与えられる圏を $`\cat{C}`$ 、得られる圏を $`\cat{D}`$ とします。その他、できる限り記号・記法を揃えます。共通に使う記法は:
- $`\mrm{Iso}(\cat{C}) = \mrm{Iso}\cat{C}`$ : 圏 $`\cat{C}`$ と同じ対象を持ち、圏 $`\cat{C}`$ のすべての同型射からなる圏(亜群になる)。
- $`\mrm{Iso}\cat{C}(X, Y)`$ : 圏 $`\cat{C}`$ の $`X \to Y`$ である同型射の集合
- $`\varphi * \hyp`$ : $`\cat{C}`$ の同型射 $`\varphi`$ による左作用
定義したホムセット上の同値関係が合同になること、定義した結合と恒等射が合同に対して法則〈概圏の公理〉を満たすことの記述・証明は割愛します。
モノイド圏における定義や計算では、ストリング図を描くことを強くオススメします。例えば、State構成における結合の定義はひどく複雑に見えますが、ストリング図を描けばどうってことない定義だと分かります。
Span構成
与えられる圏
圏 $`\cat{C}`$ はファイバー積〈プルバック | 引き戻し〉を持つとします。話を簡単にするために、モノイド積としての直積 $`\times`$ も持つとします(つまりデカルト・モノイド圏)。終対象はモノイド単位になり、終対象を余頭部〈cohead〉とするコスパンのファイバー積は直積〈デカルト・モノイド積〉と同型です。
対象集合とホムセット
$`\cat{D} := \mrm{Span}(\cat{C})`$ として、$`\cat{D}`$ の定義〈構成〉を述べていきます。
$`\Define |\cat{D}| := |\cat{C}|`$
ホムセットは以下のとおり。
$`\For A, B \in |\cat{D}|\\
\Define \cat{D}(A, B) := \sum_{X\in |\cat{D}|} \cat{C}(X, A\times B)
`$
「だいたい圏になる: 概圏」では、スパンの集合をホムセットの直積で書いていましたが、次の同型を使って変形しています。
$`\quad \cat{C}(X, A) \times \cat{C}(X, B) \cong \cat{C}(X, A\times B) \In {\bf Set}`$
$`\cat{C}`$ は局所小圏なので、$`\cat{C}(X, A\times B)`$ は小さい集合ですが、総直和(シグマ型)の構成のときに $`|\cat{D}| = |\cat{C}|`$ に渡る和を作っているので、ホムセットは真に大きい(小さくない)かも知れません。
$`\cat{D}(A, B)`$ の要素〈射〉は次の形の依存ペアで表します。
$`\quad (X, f)\\
\Where X\in |\cat{C}|, f \in \cat{C}(X, A\times B)
`$
さらに、$`f`$ はデカルト・ペアにより書けます。
$`\quad f = \langle f_1, f_2\rangle\\
\Where f_1 \in \cat{C}(X, A), f_2 \in \cat{C}(X, B)
`$
したがって、$`\cat{D}(A, B)`$ の要素は次のようにも書けます。
$`\quad (X, \langle f_1, f_2 \rangle )\\
\Where X\in |\cat{C}|, f_1 \in \cat{C}(X, A), f_2 \in \cat{C}(X, B)
`$
$`X`$ がスパンの頭部〈head〉、$`f_1`$ がスパンの左脚〈left leg〉、$`f_2`$ がスパンの右脚〈right leg〉です(「スパンの圏って定義できるの?」参照)。
同型射による作用
$`\cat{D}`$ の射に、$`\cat{C}`$ の同型射が次のように作用します。
$`\For X, Y, A, B\in |\cat{D}|\\
\For \varphi \in \mrm{Iso}\cat{C}(X, Y)\\
\For (Y, g) \in \cat{D}(A, B)\\
\Define \varphi * (Y, g) := (X, k) \;\in \cat{D}(A, B)\\
\Where k := (\varphi ; g : X \to A\times B \In \cat{C})
`$
$`\psi \in \mrm{Iso}\cat{C}(Y, Z)`$ があると、次が成立します。
$`\quad \varphi * (\psi * (Z, h)) = (\varphi ; \psi) * (Z, h)`$
同値関係
ホムセット上の同値関係 $`\sim_{A, B}`$ を次のように定義します。
$`\For A, B\in |\cat{D}|\\
\For (X, f), (Y, g) \in \cat{D}(A, B)\\
\Define (X, f) \sim_{A, B} (Y, g) :\Iff
\exists \varphi \in \mrm{Iso}\cat{C}(X, Y).\,
(X, f) = \varphi * (Y, g)
`$
恒等射と結合
恒等射は次のように定義します。
$`\For A \in |\cat{D}|\\
\Define \id_A := (A, k) \;\in \cat{D}(A, A)\\
\Where k := (\langle \id_A, \id_A \rangle : A \to A\times A \In \cat{C})
`$
結合に関しては「スパンの圏って定義できるの?」を見てください。
Env構成
与えられる圏
圏 $`\cat{C}`$ はモノイド圏 $`\cat{C} = (\cat{C}, \otimes, I, \alpha, \lambda, \rho)`$ (記号の乱用)とします。モノイド圏が対称である必要はありません。
対象集合とホムセット
$`\cat{D} := \mrm{Env}(\cat{C})`$ として、$`\cat{D}`$ の定義〈構成〉を述べていきます。
$`\Define |\cat{D}| := |\cat{C}|`$
ホムセットは以下のとおり。
$`\For A, B \in |\cat{D}|\\
\Define \cat{D}(A, B) := \sum_{X\in |\cat{D}|} \cat{C}(X\otimes A, B)
`$
$`\cat{C}`$ は局所小圏なので、$`\cat{C}(X\otimes A, B)`$ は小さい集合ですが、総直和(シグマ型)の構成のときに $`|\cat{D}| = |\cat{C}|`$ に渡る和を作っているので、ホムセットは真に大きい(小さくない)かも知れません。
$`\cat{D}(A, B)`$ の要素〈射〉は次の形の依存ペアで表します。
$`\quad (X, f)\\
\Where X\in |\cat{C}|, f \in \cat{C}(X\otimes A, B)
`$
$`(X, f)`$ を環境付き射〈morphism with environment〉と呼び、$`X`$ は環境対象〈environment object〉と呼びます。今回の定義では環境対象が左にありますが、右環境対象と右環境付き射も同様に定義できます。(右にしたほうが良かった気もしてます。)
同型射による作用
$`\cat{D}`$ の射に、$`\cat{C}`$ の同型射が次のように作用します。
$`\For X, Y, A, B\in |\cat{D}|\\
\For \varphi \in \mrm{Iso}\cat{C}(X, Y)\\
\For (Y, g) \in \cat{D}(A, B)\\
\Define \varphi * (Y, g) := (X, k) \;\in \cat{D}(A, B)\\
\Where k := ( ( \varphi \otimes \id_A) ; g : X\otimes A \to B \In \cat{C} )
`$
$`\psi \in \mrm{Iso}\cat{C}(Y, Z)`$ があると、次が成立します。
$`\quad \varphi * (\psi * (Z, h)) = (\varphi ; \psi) * (Z, h)`$
同値関係
ホムセット上の同値関係 $`\sim_{A, B}`$ を次のように定義します。
$`\For A, B\in |\cat{D}|\\
\For (X, f), (Y, g) \in \cat{D}(A, B)\\
\Define (X, f) \sim_{A, B} (Y, g) :\Iff
\exists \varphi \in \mrm{Iso}\cat{C}(X, Y).\,
(X, f) = \varphi * (Y, g)
`$
恒等射と結合
恒等射は次のように定義します。
$`\For A \in |\cat{D}|\\
\Define \id_A := (I, k) \;\in \cat{D}(A, A)\\
\Where k := ( \lambda_A : I\otimes A \to A \In \cat{C} )
`$
結合は次のように定義します。
$`\For A, B, C \in |\cat{D}|\\
\For (X, f) \in \cat{D}(A, B)\\
\For (Y, g) \in \cat{D}(B, C)\\
\Define (X, f); (Y, g) := (Y\otimes X, k)\; \in \cat{D}(A, C)\\
\Where k := (\alpha_{Y, X, A}; (\id_Y\otimes f) ; g : (Y\otimes X)\otimes A \to C \In \cat{C})
`$
厳密モノイド圏なら、定義は簡単になります。
State構成
与えられる圏
圏 $`\cat{C}`$ は対称モノイド圏 $`\cat{C} = (\cat{C}, \otimes, I, \alpha, \lambda, \rho, \sigma)`$ (記号の乱用)とします。
対象集合とホムセット
$`\cat{D} := \mrm{State}(\cat{C})`$ として、$`\cat{D}`$ の定義〈構成〉を述べていきます。
$`\Define |\cat{D}| := |\cat{C}|`$
ホムセットは以下のとおり。
$`\For A, B \in |\cat{D}|\\
\Define \cat{D}(A, B) := \sum_{X\in |\cat{D}|} \cat{C}(X\otimes A, X\otimes B)
`$
$`\cat{C}`$ は局所小圏なので、$`\cat{C}(X\otimes A, X\otimes B)`$ は小さい集合ですが、総直和(シグマ型)の構成のときに $`|\cat{D}| = |\cat{C}|`$ に渡る和を作っているので、ホムセットは真に大きい(小さくない)かも知れません。
$`\cat{D}(A, B)`$ の要素〈射〉は次の形の依存ペアで表します。
$`\quad (X, f)\\
\Where X\in |\cat{C}|, f \in \cat{C}(X\otimes A, X\otimes B)
`$
$`(X, f)`$ を状態付き射〈morphism with state〉と呼び、$`X`$ は状態対象〈state object〉と呼びます。今回の定義では状態対象が左にありますが、右状態対象と右状態付き射も同様に定義できます。(右にしたほうが良かった気もしてます。)
同型射による作用
$`\cat{D}`$ の射に、$`\cat{C}`$ の同型射が次のように作用します。
$`\For X, Y, A, B\in |\cat{D}|\\
\For \varphi \in \mrm{Iso}\cat{C}(X, Y)\\
\For (Y, g) \in \cat{D}(A, B)\\
\Define \varphi * (Y, g) := (X, k) \;\in \cat{D}(A, B)\\
\Where k := ( ( \varphi \otimes \id_A) ; g ;(\varphi^{-1} \otimes \id_B) : X\otimes A \to X \otimes B \In \cat{C} )
`$
$`\psi \in \mrm{Iso}\cat{C}(Y, Z)`$ があると、次が成立します。
$`\quad \varphi * (\psi * (Z, h)) = (\varphi ; \psi) * (Z, h)`$
同値関係
ホムセット上の同値関係 $`\sim_{A, B}`$ を次のように定義します。
$`\For A, B\in |\cat{D}|\\
\For (X, f), (Y, g) \in \cat{D}(A, B)\\
\Define (X, f) \sim_{A, B} (Y, g) :\Iff
\exists \varphi \in \mrm{Iso}\cat{C}(X, Y).\,
(X, f) = \varphi * (Y, g)
`$
恒等射と結合
恒等射は次のように定義します。
$`\For A \in |\cat{D}|\\
\Define \id_A := (I, k) \;\in \cat{D}(A, A)\\
\Where k := ( \id_I \otimes \id_A : I\otimes A \to I\otimes A \In \cat{C} )
`$
結合は次のように定義します。
$`\For A, B, C \in |\cat{D}|\\
\For (X, f) \in \cat{D}(A, B)\\
\For (Y, g) \in \cat{D}(B, C)\\
\Define (X, f); (Y, g) := (Y\otimes X, k)\; \in \cat{D}(A, C)\\
\Where k := (\\
\quad \alpha_{Y, X, A}; (\id_Y \otimes f) ; (\id_Y \otimes \sigma_{X, B}) ;
(\alpha_{Y, B, X})^{-1} ; (g \otimes \id_X) ; \alpha_{Y, C, X} ;
(\id_Y \otimes \sigma_{C, X} ) ; (\alpha_{Y, X, C})^{-1}\\
\quad : (Y\otimes X)\otimes A \to (Y\otimes X) \otimes C \In \cat{C}\\
)
`$
この定義は、次のストリング図から写し取ったものです。
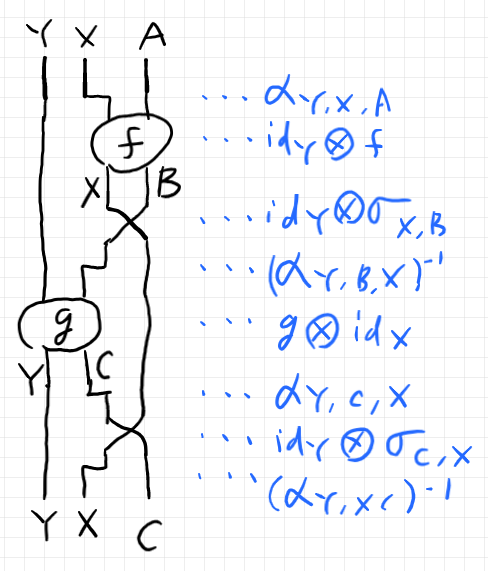
対称厳密モノイド圏なら、定義は簡単になります。結合律子〈一貫性同型射〉 $`\alpha`$ が不要になります。
$`\quad (\id_Y \otimes f) ; (\id_Y \otimes \sigma_{X, B}) ;
(g \otimes \id_X) ;
(\id_Y \otimes \sigma_{C, X} )`$