次の論文の内容で、僕が「面白いな」と思った点を幾つかピックアップして紹介します。
- Title: String Diagrams for Layered Explanations
- Author: Leo Lobski, Fabio Zanasi
- Submitted: 8 Jul 2022
- Pages: 21p
- URL: https://arxiv.org/abs/2207.03929
科学的説明〈scientific explanation〉において、層化した〈layered〉ストリング図が有効に使えるよ、ってことが、この論文の眼目です。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\twoto}{\Rightarrow}
\newcommand{\hyp}{\text{-}}
\newcommand{\In}{\text{ in }}
`$
内容:
裏返し反変関手
ロブスキ/ザンサイ〈Leo Lobski, Fabio Zanasi〉は、層化プロップ〈layered prop〉という概念を導入してますが、これは(おそらく意図的に)構文論と意味論がゴッチャになっています。意味論側だけを切り出すと、インデックス付き圏〈indexed category〉です。ただし、最初に余インデックス付き圏(共変関手)を出して、後からインデックス付き圏〈反変関手〉を追加する構成になっています。
反変・共変の別で混乱しがちなので、そこを先に片付けておきましょう。明示的に次の反変関手を使います。
$`\quad \mrm{Rev}_\cat{C} : \cat{C} \to \cat{C}^\mrm{op}`$ (反変関手)
任意の反変関手 $`G`$ は、この反変関手(裏返し〈reversing〉)の後に共変関手 $`F`$ を結合して表せます(下の図)。
$`\xymatrix{
{\cat{C}} \ar[r]^{\mrm{Rev}_\cat{C}} \ar[dr]_{G}
& {\cat{C}^\mrm{op}} \ar[d]^{F}
\\
{}
& {\cat{D}}
}\\
\text{commutative}`$
$`\mrm{Rev}_\cat{C}`$ は厳密に可逆な関手で、次が成立します。
$`\quad {\mrm{Rev}_\cat{C}}^{-1} = \mrm{Rev}_{\cat{C}^\mrm{op}}`$
また、$`G:\cat{C}\to \cat{D}`$ (反変でも共変でもよい)に対して次のように定義します。アスタリスクは、関手の図式順結合記号です。
$`\quad {^\mrm{rev} G} := \mrm{Rev}_{\cat{C}^\mrm{op}} * G : \cat{C}^\mrm{op} \to \cat{D}\\
\quad G^\mrm{rev} := G * \mrm{Rev}_{\cat{D}} : \cat{C} \to \cat{D}^\mrm{op}
`$
すると、次が成立します。
- $`G`$ が反変関手のとき、$`{^\mrm{rev}G}`$ は共変関手になる。
- $`G`$ が共変関手のとき、$`{^\mrm{rev} G}`$ は反変関手になる。
- $`G`$ が反変関手のとき、$`{G^\mrm{rev}}`$ は共変関手になる。
- $`G`$ が共変関手のとき、$`{ G^\mrm{rev}}`$ は反変関手になる。
よく使うのは一番目の事実で、しばしば、反変関手 $`G`$ と共変関手 $`{^\mrm{rev}G}`$ を同一視します。つまり、共変関手 $`F:\cat{C}^\mrm{op} \to \cat{D}`$ を「$`\cat{C}`$ から $`\cat{D}`$ への反変関手」と呼びます。
通常、“圏の圏”として使っている $`{\bf Cat}`$ や $`{\bf CAT}`$ には表立っては反変関手は存在してなくて(文字通り「裏の存在」)、代わりに $`\cat{C}^\mrm{op} \to \cat{C}`$ を使おう、という習慣です。
余インデックス付き対称厳密モノイド圏
小さな対称厳密モノイド圏を対象として、対称モノイド圏の構造をすべて厳密に〈on the nose で〉保存する関手を射とする圏を $`{\bf SymStrMonCat}^1`$ とします。右肩の 1 は、自然変換は考えてなくて1-圏であることを示します。
$`\cat{C}`$ を任意の圏として、次の関手を余インデックス付き対称厳密モノイド圏〈coindexed symmetric strict monoidal category〉と呼びます。
$`\quad \cat{M} : \cat{C} \to {\bf SymStrMonCat}^1 \In {\bf CAT}`$
反変関手ならインデックス付き対称厳密モノイド圏〈indexed symmetric strict monoidal category〉です。
$`\cat{M}`$ が余インデックス付き対称厳密モノイド圏なら、$`{^\mrm{rev}\cat{M}}`$ はインデックス付き対称厳密モノイド圏です。
$`\quad {^\mrm{rev}\cat{M}} : \cat{C}^\mrm{op} \to {\bf SymStrMonCat}^1 \In {\bf CAT}`$
ベース圏〈インデキシング圏〉$`\cat{C}`$ が次のような特別な場合を考えます。
- $`\cat{C}`$ は小さい圏である。
- $`\cat{C}`$ はとてもやせた圏〈順序集合〉である。
- $`\cat{C}`$ は始対称を持つ。
つまり、$`\cat{C}`$ は最小元を持つ順序集合です。このようなベース圏をロブスキ/ザンサイ論文に倣って $`\Omega`$ と書きます。ベース圏 $`\Omega`$ の対象は $`\omega, \tau`$ などのギリシャ文字小文字で表し、射は $`f, g`$ などのラテン文字小文字で表します。始対象は $`\bot`$ で書きます*1。
射 $`f:\omega \to \tau \In \Omega`$ は、$`\omega, \tau`$ のあいだの順序なので、次のようにも書きます。
$`\quad f = (\omega \le \tau) : \omega \to \tau \In \Omega`$
同じ射 $`f`$ を反対圏 $`\Omega^\mrm{op}`$ で考えたものは次のようにも書きます。
$`\quad f = (\tau \ge \omega) : \tau \to \omega \In \Omega^\mrm{op}`$
余インデックス付き圏/インデックス付き圏の共変関手/反変関手は次の記法を使います。これも、ロブスキ/ザンサイ論文からです*2。
$`\quad \omega \blacktriangleleft \tau := \cat{M}[(\omega \le \tau)] :
\cat{M}[\omega] \to \cat{M}[\tau] \In {\bf SymStrMonCat}^1\\
\quad \tau \triangleright \omega := {^\mrm{rev}\cat{M}}[(\tau \ge \omega )] :
{^\mrm{rev}\cat{M}}[\omega] \to {^\mrm{rev}\cat{M}}[\tau] \In {\bf SymStrMonCat}^1
`$
$`\omega \blacktriangleleft \tau`$ と $`\tau \triangleright \omega`$ はまったく同じ関手です。関手のベース射の方向を裏返して考えるだけです。
層化プロップ
プロップ〈PROP〉は、多圏の仲間とみなすとモノイド積をもつ多圏です。「述語論理: 様々な多圏達の分類整理」に書いたように、「プロップ〈PROP〉 = 対称・モノイド・ワイド多圏」です。"PROP" は "product and permutation category" に由来します。
対称・モノイド・ワイド多圏は対称厳密モノイド圏ともみなせるので、対称厳密モノイド圏をプロップと呼ぶこともあります(用語運用は曖昧です)。
ロブスキ/ザンサイ論文における層化プロップ〈layered prop〉は、余インデックス付き対称厳密モノイド圏のことですが、その構文論と意味論も含めた呼称のようです。
モノイド圏の対象・射を表現する書き表し方には、テキストと絵図〈picture | diagram〉があります。絵図も表現なので構文(語彙と文法)を持ちます。
- テキスト構文: 文字・記号の1次元的組み合わせ方の規則
- 絵図構文: 図形の2次元または3次元的組み合わせ方の規則
テキスト構文は多次元情報を潰して難読化してしまうので、絵図構文だけを考えます。ロブスキ/ザンサイ論文が提案しているのも絵図構文です。例えば次は、ストリング図の変形〈描き換え〉の規則です。
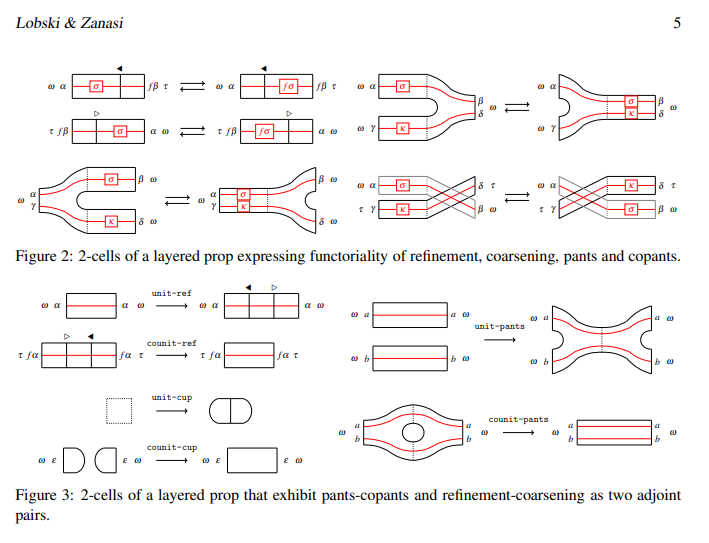
ロブスキ/ザンサイの絵図構文は、従来からよく使われているストリング図描画法に、次の描画規則を加えたものです。
- ベース圏の対象 $`\omega \in |\Omega|`$ ごとにキャンバスを準備する。複数のキャンバスを同時に使う。
- 関手ボックスの変種としてウィンドウ〈関手コボックス〉も使う。
- 関手ボックスの変種としてスプリッター図も使う。
新規な描画法については後述することにして、ロブスキ/ザンサイに独特な用語と解釈を説明します; 余インデックス付き圏 $`\cat{M}`$ のベース圏 $`\Omega`$ の対象は、現象を観測する視点や手法だと解釈・想定します。視点・手法 $`\omega \in |\cat{\Omega}|`$ で観測した現象モデルが対称厳密モノイド圏 $`\cat{M}[\omega]`$ です。
ベース圏の射 $`f:\omega \to \tau`$ は詳細化〈refinement〉と呼びます。共変的に誘導される関手 $`\omega \blacktriangleleft \tau = \cat{M}[f]`$ も詳細化と呼びます。ベース圏の反対圏の射は粗視化〈coarsening〉です。反変的に誘導される関手 $`\tau \triangleright \omega = {^\mrm{rev}\cat{M}}[f]`$ も粗視化と呼びます。
以上の用語は、抽象的構造やその構成素に付けられた名前に過ぎないので、比喩的な意味に引きずられないように注意してください。例えば「詳細化」は、「ベース圏の射」と「誘導された関手」の別名というだけで、それ以上の意味は持ちません。
絵図構文〈描画規則〉に従って描かれた絵図が指し示す対象物〈denotation〉は、余インデックス付き圏/インデックス付き圏のグロタンディーク構成のトータル圏(「最近の型理論: 拡張包括構造を持ったインデックス付き圏」の最初の節参照)の射です。
関手コボックスとスプリッター図
ロブスキ/ザンサイの描画方向は、射の方向が右から左、モノイド積の方向が上から下ですが、僕の説明は射の方向が上から下、モノイド積の方向は左から右です。描画方向やその変換は次の記事を参照してください。
ストリング図、関手ボックス、ストライプ図などに関しては、このブログ内に山のように関連記事があります。
入門的記事をひとつだけ挙げれば:
さて、関手ボックスは、関手 $`F:\cat{C} \to \cat{D}`$ に対してボックス〈箱〉を描きます。
- ボックスの内部には圏 $`\cat{C}`$ のストリング図を描く。
- ボックスの外部(キャンバスの地)は圏 $`\cat{D}`$ を表す。
一方、$`F`$ の関手コボックス〈functor cobox〉は:
- ボックスの内部には圏 $`\cat{D}`$ のストリング図を描く。
- ボックスの外部(キャンバスの地)は圏 $`\cat{C}`$ を表す。
(左が関手ボックスで右が関手コボックス)
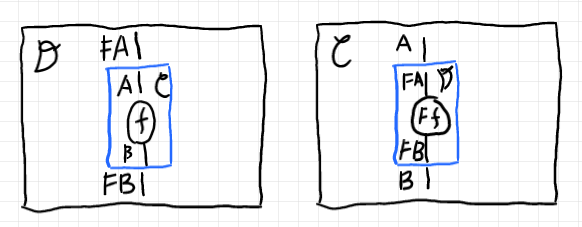
ロブスキ/ザンサイ論文では、関手コボックスをウィンドウ〈window〉、関手ボックスをコウィンドウ〈cowindow〉と呼んでいます。
関手ボックスの変種として次があります。
1. ボックスの高さ(射の方向の寸法)をキャンバスの高さと同じにする。(ストライプ図)
2. ボックスの幅(モノイド積の方向の寸法)をキャンバスの幅と同じにする。
3. ボックスをキャンバスを二分する矩形として描く。(スプリッター図)
(左上がストライプ図、下の2つはスプリッター図)
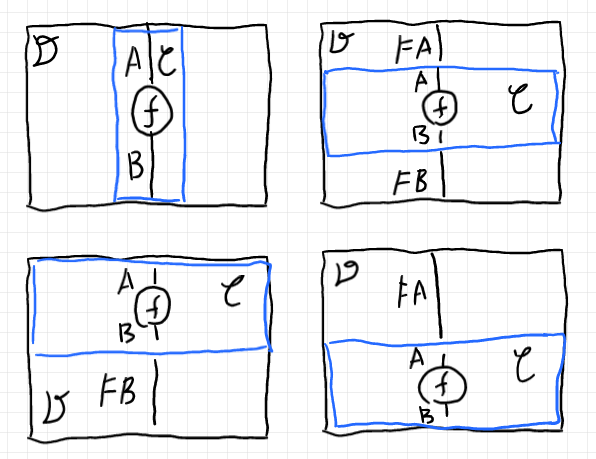
関手コボックスに対しても同様な変種を考えることができます。
スプリッター図を使うと、関手ボックス/関手コボックスと同様な描画が入れ子にならずに描けます。異なる圏を描くキャンバスを併置接合したように見えます。ロブスキ/ザンサイのアイディアは、層化プロップのトータル射を、複数のキャンバス矩形とスプリッター図を使って描こうということです。入れ子がないとレイアウトの複雑度が減少します。
おわりに
ロブスキ/ザンサイ論文の興味深い部分は、後半の応用事例でしょう。システム生物学、電気回路網、並列処理プログラミングからの例題があります。複数の視点・手法に基づく複数の圏にまたがる射を視覚化して計算するには、層化ストリング図は有効そうです。演繹系や型理論の観点からも、層化プロップ/層化ストリング図は面白い対象物だと思います。