「圏論におけるフレーム充填問題」で、二重圏や2-圏におけるフレーム充填問題の事例を挙げました。1-圏、つまり通常の圏でもフレーム充填問題とその解を考えることができます。
通常の圏における重要な概念も、フレーム充填問題の“最良の解”として定義できます。$`\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\dblcat}[1]{\mathbb{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\twoto}{ \Rightarrow }
`$
内容:
1-圏の2-射
通常の圏〈1-圏〉にも2-射はあります。1-圏の2-射とは、射のあいだの等式のことです。$`f, g : A \to B`$ が圏 $`\cat{C}`$ の2つの射だとして、$`f`$ から $`g`$ への2-射は次の等式です。
$`\quad f = g \;: A \to B \In \cat{C}`$
「$`f`$ と $`g`$ が等しい」ことに $`\alpha`$ という名前を付けて、向きも明示するなら、次の書き方になります。
$`\quad \alpha :: f \twoto g : A \to B \In \cat{C}`$
等式は、“可逆な2-射”なので、次のようにも書けます。
$`\quad \alpha^{-1} :: g \twoto f : A \to B \In \cat{C}`$
次のような可換図式があったとしましょう。
$`\quad \xymatrix {
A \ar[r]^{f} \ar[d]_{g}
& B \ar[d]^{g'}
\\
C \ar[r]_{f'}
& D
}\\
\quad \text{commutative }\In \cat{C}
`$
これは、以下のように書いても同じです。$`\alpha`$ は2-射、つまり等式です。
$`\quad \xymatrix@C+1pc {
{}
& B \ar@/^/[dr]^{g'} \ar@{}[dd]|{\alpha\,\Downarrow\:}
& {}
\\
A \ar@/^/[ur]^{f} \ar@/_/[dr]_{g}
& {}
& D
\\
{}
& C \ar@/_/[ur]_{f'}
& {}
}\\
\quad \In \cat{C}
`$
テキストで書くなら:
$`\quad \alpha :: f;g' \twoto g;f' : A \to D \In \cat{c}`$
2-射の向きを逆転させても言ってること(等しさの主張)は同じです。
$`\quad \alpha^{-1} :: g;f' \twoto f;g' : A \to D \In \cat{c}`$
射のあいだの等式を2-射として扱うことは、1-圏と2-圏を統一的に扱う第一歩になります。
フレーム充填問題としてのプルバック構成
通常の圏 $`\cat{C}`$ におけるプルバック構成〈pullback construction〉を、コスパンの充填問題と考えましょう。黒が既知〈所与〉のフレーム(今はコスパン)、紫が未知項です。
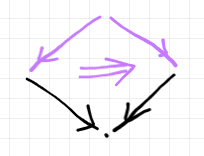
0-射〈対象〉、1-射〈射〉、2-射〈等式〉にラベル付けすると次のようです。未知項のラベルは疑問符を後置してます。
$`\quad \xymatrix {
{}
& P? \ar[dl]_{p?} \ar[dr]^{q?}
& {}
\\
A \ar[dr]_{f} \ar@{}[rr]|{\alpha?\,\Rightarrow}
& {}
& B \ar[dl]^{g}
\\
{}
& C
& {}
}\\
\quad \In \cat{C}
`$
このコスパン充填問題 $`\text{cospan-fill}`$ をテキストで記述するなら:
$`\text{cospan-fill}\\
\quad \alpha? :: p?;f \twoto q?;g : P? \to C\\
\text{where}\\
\quad A, B, C, P? \in |\cat{C}|\\
\quad f: A \to C \In \cat{C}\\
\quad g: B \to C \In \cat{C}\\
\quad p?: P? \to A \In \cat{C}\\
\quad q?: P? \to B \In \cat{C}
`$
コスパン充填問題 $`\text{cospan-fill}`$ の解空間(「圏論におけるフレーム充填問題」参照)は $`\mrm{Sol}(\text{cospan-fill})`$ です。
コスパン充填問題 $`\text{cospan-fill}`$ の解空間 $`\mrm{Sol}(\text{cospan-fill})`$ には、たくさんの解(空間の点)が含まれるかも知れませんが、我々が興味を持つのは“最良の解”です。最良の解で埋めた四角形(四辺形ではない! 「圏論におけるフレーム充填問題」参照)が、プルバック四角形〈pullback square〉です。
コスパン・フィラーの比較
コスパン充填問題の解は、コスパン・フィラー〈cospan filler〉とも呼びます。圏 $`\cat{C}`$ 内に与えられたコスパン $`A\overset{f}{\to} C \overset{g}{\leftarrow} B`$ に対して、2つのコスパン・フィラーがあったとします。以下のように。
$`\quad \xymatrix {
{}
& P \ar[dl]_{p} \ar[dr]^{q}
& {}
\\
A \ar[dr]_{f} \ar@{}[rr]|{\alpha\,\Rightarrow}
& {}
& B \ar[dl]^{g}
\\
{}
& C
& {}
}
\quad\xymatrix {
{}
& R \ar[dl]_{r} \ar[dr]^{s}
& {}
\\
A \ar[dr]_{f} \ar@{}[rr]|{\beta\,\Rightarrow}
& {}
& B \ar[dl]^{g}
\\
{}
& C
& {}
}\\
\quad \In \cat{C}
`$
コスパン・フィラー $`\alpha, \beta`$ とは、圏 $`\cat{C}`$ の2-射です。コスパン充填問題の解空間 $`\mrm{Sol}(\text{cospan-fill})`$ (の台集合)は、2-射の集合だと言えます*1。
我々は最良のコスパン・フィラー(特別な2-射)に興味があるので、2つのコスパン・フィラーのどちらが良いかを比較する必要があります。フィラーどうし(今は $`\alpha`$ と $`\beta`$)を比較するためにも再びフィラーを使います。以下のようなフレーム充填問題のフィラー〈解〉を考えるのです。
$`\quad \xymatrix@C+1pc {
{}
& P \ar[dl]_{p} \ar[dr]^{q} \ar@{}@/_1pc/[dd]_{?\Rightarrow} \ar[dd]|{?} \ar@{}@/^/[dd]^{?\Rightarrow}
& {}
\\
A \ar[dr]_{r}
& {}
& B \ar[dl]^{s}
\\
{}
& R
& {}
}
`$
このフレーム(対角線付き四辺形)充填問題の解〈フィラー〉もたくさんあるでしょうが、次の等式も制約として付け加えます。
$`\quad \alpha =
\xymatrix@C+2pc{
{}
& P \ar@/_/[ddl]_{p} \ar@/^/[ddr]^{q} \ar[d]|{?}
\ar@{}@/^/[ddl]|{?\Rightarrow} \ar@{}@/_/[ddr]|{?\Rightarrow}
& {}
\\
{}
& R \ar[dl]^{r} \ar[dr]_{s}
& {}
\\
A \ar[dr]_{f} \ar@{}[rr]|{\beta\,\Rightarrow\:}
& {}
& B \ar[dl]^{g}
\\
{}
& C
& {}
}\\
\quad \In \cat{C}
`$
上の図式の等式で表現される状況を、記号的に次のように表現しましょう。
$`\quad \alpha = \xi? \circledast \beta`$
ここで、$`\xi?`$ は図式の未知部分(疑問符のところ)を代表的に表している未知項です。$`\circledast`$ は、$`\xi?`$ と $`\beta`$ の“組み合わせ方”を一文字で表した演算子記号です。$`\circledast`$ が表す演算は、$`\xi?`$ と $`\beta`$ の共通の境界線である $`r, s`$ を糊しろにして張り合わせる操作です。
$`\xi`$(疑問符なし)が、実際のフィラーだとすると、次の等式が成立します。
$`\quad \alpha = \xi \circledast \beta`$
$`\circledast`$ を一種の掛け算と考えると、上の等式は、$`\alpha`$ を2つの因子〈factor〉に因子分解〈factorization〉しているとみなせます。
与えられた2つのフィラー $`\alpha, \beta`$ に対して、フィラーのあいだのフィラーである $`\xi`$ は、$`\alpha`$ と $`\beta`$ の違い・隔たりを測る量だとも言えます。$`\beta`$ に、$`\xi`$ を(左から)掛けることにより $`\alpha`$ が得られるので、$`\alpha`$ と $`\beta`$ は $`\xi`$ 分だけの違い・隔たりがあるわけです。$`\xi`$ は2つのフィラーを比較して、その違い・隔たりを表現するモノなので、比較子〈comparator〉と呼ぶことにします。
$`\beta`$ に、$`\xi`$ を掛けることにより $`\alpha`$ が得られることを、次のように書いてみましょう。
$`\quad \xi : \alpha \to \beta`$
こう書くと、フィラーのあいだの比較子 $`\xi`$ が、2つのフィラー $`\alpha, \beta`$ のあいだの射であるように思えます。実際に、コスパン・フィラー達を対象として、フィラーのあいだの比較子を射とする圏が存在します。
コスパン充填問題の解空間 $`\mrm{Sol}(\text{cospan-fill})`$ は、単にフィラー(である2-射)の集合なだけではなくて、圏の構造を持つのです。圏であることを強調したいときは $`\cat{Sol}(\text{cospan-fill})`$ と書くことにします(一時的な表記ルールですが)。$`\cat{Sol}(\text{cospan-fill})`$ は、コスパン充填問題の解の圏です。
極限(「圏論の極限を具体的に」参照)についてご存知なら、圏 $`\cat{Sol}(\text{cospan-fill})`$ が、コスパンを底面とする錐〈cone〉の圏 $`\mrm{Cone}_{\text{cospan}}`$ と事実上同じものであることがわかるでしょう。$`\cat{Sol}(\text{cospan-fill})`$ と $`\mrm{Cone}_{\text{cospan}}`$ の対応を確認するのは良い練習問題だと思います。
ペースティング図からストリング図へ
ここで、ペースティング図をストリング図に描き変える練習をしてみましょう。$`\alpha, \beta`$ がコスパン・フィラーだとして、$`\xi`$ は2つのコスパン・フィラーのあいだの比較子です。これは、次のような因子分解の等式が成立していることでもあります。
$`\quad \alpha = \xi \circledast \beta`$
$`\alpha`$ を黒、$`\beta`$ を青、$`\xi`$ を赤で描くとして、ペースティング図の等式は次のようになります。ラベルは省略します。
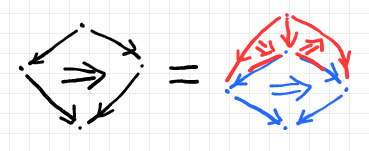
2-射の向きが上から下になるように90度回転すると次のようです。
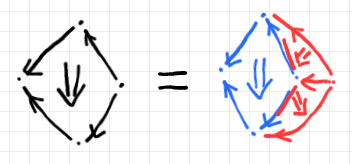
1-射の向きが左から右になるように鏡映変換すると:
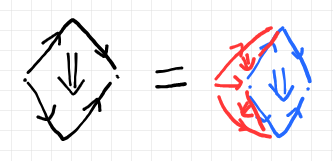
上記ペースティング図のポアンカレ双対をとると、ストリング図のあいだの等式になります。描画方向は、1-射の結合の方向が左から右、2-射の方向が上から下です。
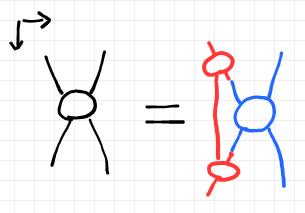
風変わりな演算子記号 $`\circledast`$ の意味は次のように定義できます。
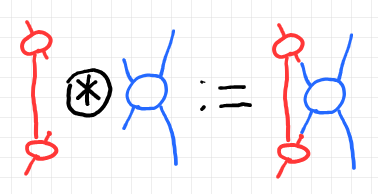
コスパン・フィラー $`\alpha`$ が、比較子 $`\xi`$ とコスパン・フィラー $`\beta`$ に因子分解できることが、コスパン充填問題の解の圏 $`\cat{Sol}(\text{cospan-fill})`$ の射を定義するので、以下が成立します。
$`\quad (\alpha = \xi \circledast \beta) \iff (\xi :\alpha \to \beta \In \cat{Sol}(\text{cospan-fill}))`$
最良のコスパン・フィラー
与えられたコスパンに対するプルバック四角形とは、最良のコスパン・フィラーのことです。コスパン・フィラーは、コスパン充填問題の解の圏 $`\cat{Sol}(\text{cospan-fill})`$ の対象です。対象達は、射〈比較子〉により互いに比較することができます。つまり、“良さ”を評価できます。最も良いコスパン・フィラーとは、圏 $`\cat{Sol}(\text{cospan-fill})`$ の終対象のことです。
$`\omega`$ を圏 $`\cat{Sol}(\text{cospan-fill})`$ の終対象とすると、任意の対象〈コスパン・フィラー〉 $`\alpha`$ から $`\omega`$ への射〈比較子〉が一意的に存在します。終対象への一意的な射は、$`!_\alpha`$ と書くのが習慣です。
$`\quad !_\alpha : \alpha \to \omega \In \cat{Sol}(\text{cospan-fill})`$
これは、次のような因子分解が一意的に可能なことです。
$`\quad \alpha =\; !_\alpha \circledast \omega`$
$`\circledast`$ を一種の掛け算とみなすなら、$`\omega`$ による割り算(仮に $`\oslash`$ とする)ができて、商が一意的に決まることになります。
$`\quad !_\alpha := \alpha \oslash \omega\\
\quad \alpha =\; !_\alpha \circledast \omega\\
\text{i.e. }\\
\quad \alpha = (\alpha \oslash \omega) \circledast \omega
`$
最良のコスパン・フィラーは、任意のフィラーに対する一意的な因子分解可能性(一意的商の存在)によって特徴付けられます。
最良のコスパン・フィラーとは、コスパンの極限錐のことであり、錐の圏の終対象のことです。コスパン充填問題は、極限の定義を言い換えているだけとも言えますが、極限に対する違った視点を与える点で意義があります。
*1:2-射を組み合わせた図式の集合と言ったほうがより正確かも知れません。