「添加仮想二重圏」において、「フレーム」という言葉を出しました。フレームは、2-射(2次元の射)の境界のことです。境界は幾つかの1-射達/0-射達の組み合わせです。境界全体ではなくて、境界の一部分のことも「フレーム」と呼ぶことにすると、与えられたフレーム(境界の一部)に対して、残りの部分を充填〈filling〉して2-射を完成させる、という問題を考えることができます。このタイプの問題をフレーム充填問題と呼びましょう。
二重圏や2-圏における重要な概念は、フレーム充填問題の解、特に“最良な解”として定義できることが多くあります。この記事では、二重圏のニッチ〈niche〉*1と2-圏のスパンを事例として、圏論におけるフレーム充填問題を説明します。
フレーム充填問題に関連して、意味は変えないで図式の描画法やレイアウトを変える作業がよく出てきます。これについても述べます。$`\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\dblcat}[1]{\mathbb{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\twoto}{ \Rightarrow }
`$
内容:
n辺形とn角形
三辺形/四辺形と言った場合は、内部を持たない1次元の図形を意味することにします。三角形/四角形と言った場合は、内部領域を含む2次元の図形のことです。n ≧ 5 の場合でも、n辺形とn角形の区別は同様です。
n = 2 のときもニ辺形とニ角形を考えることができます。ニ辺形とは以下のような図形です。頂点が2つあり、2本の辺には $`f, g`$ でラベルしています。内部の2次元領域は含んでない図形とします。
$`\quad \xymatrix@C+1.5pc{
\cdot \ar@{-}@/^1pc/[r]^{f} \ar@{-}@/_1pc/[r]_{g}
& \cdot
}`$
以下の図の $`\alpha`$ は、2次元領域に付けられたラベルで、$`f, g, \alpha`$ でニ角形を表しています。
$`\quad \xymatrix@C+1.5pc{
\cdot \ar@{-}@/^1pc/[r]^{f} \ar@{-}@/_1pc/[r]_{g} \ar@{}[r]|{\alpha}
& \cdot
}`$
円周〈circle〉上にただひとつの頂点を指定すると、それは一辺形になります。頂点をひとつ持つ円周の内部を埋めた円板〈disc | disk〉は一角形です。頂点を尖らせた一角形はしずく形〈teardrop〉です。
四角形、二重射、フレーム
次の図は、$`\phi`$ を内部領域とする四角形です。
$`\quad \xymatrix{
\cdot \ar@{-}[r] \ar@{-}[d] \ar@{}[dr]|{\phi}
&\cdot \ar@{-}[d]
\\
\cdot \ar@{-}[r]
&\cdot
}
`$
これを二重圏の2-射〈二重射〉の絵にしましょう。二重圏に関しては次の過去記事などを参照してください。
- 二重圏の具体的な定義(2013年)
- 二重圏の簡単な例:非負行列の順序構造(2013年)
- 二重圏を語るために(2022年)
- 二重圏、縦横をもう一度(2024年)
二重圏にはニ種類の1-射があります。それをプロ射とタイト射とします(「二重圏、縦横をもう一度」参照)。プロ射の方向を横方向、タイト射の方向を縦方向と決めましょう。そして、プロ射は破線で示すことにします。
$`\quad \xymatrix{
\cdot \ar@{--}[r] \ar@{-}[d] \ar@{}[dr]|{\phi}
&\cdot \ar@{-}[d]
\\
\cdot \ar@{--}[r]
&\cdot
}
`$
プロ射の向きは左から右、タイト射の向きは上から下として矢印にします。
$`\quad \xymatrix{
\cdot \ar@{-->}[r] \ar[d] \ar@{}[dr]|{\phi}
&\cdot \ar[d]
\\
\cdot \ar@{-->}[r]
&\cdot
}
`$
2-射を表す領域にも向きを持たせて、二重矢印で表します。
$`\quad \xymatrix{
\cdot \ar@{-->}[r] \ar[d] \ar@{}[dr]|{\phi\,\Downarrow\:}
&\cdot \ar[d]
\\
\cdot \ar@{-->}[r]
&\cdot
}
`$
4つの0-射〈対象〉と4本の1-射(プロ射が2本とタイト射が2本)とひとつの2-射〈二重射〉にラベルを付けます(2-射のラベルは既に付いてましたが)。
$`\quad \xymatrix{
A \ar@{-->}[r]^{p} \ar[d]_{f} \ar@{}[dr]|{\phi\,\Downarrow\:}
&C \ar[d]^{g}
\\
B \ar@{-->}[r]_{q}
& D
}
`$
上の図の状況をテキストで書くときは次のように書くことにします(「添加仮想二重圏」で導入した記法)。
$`\quad \phi :: f[p\twoto q]g \In \dblcat{D}`$
ここで、$`\In \dblcat{D}`$ は、2-射 $`\phi`$ やフレームを構成する1-射、0-射は $`\dblcat{D}`$ という二重圏に所属してることを示しています。0-射〈対象〉の情報まで記入するなら:
$`\quad \phi :: (f:A \to B)[p\twoto q](g: C \to D) \In \dblcat{D}`$
この記法で、$`f[p\twoto q]g`$ は2-射 $`\phi`$ の境界を表します。境界をフレーム〈frame〉ともいいます。境界全体だけでなく、境界の一部もフレームと呼ぶことにします。区別したいときは、全フレーム〈entire frame〉、部分フレーム〈partial frame〉とします。以下、単に「フレーム」といったら部分フレームのことです。プロファイル〈profile〉は全フレームの同義語です。
例えば、次は2-射 $`\phi`$ のとあるフレーム〈部分フレーム〉だけを描いたものです。
$`\quad \xymatrix{
A \ar[d]_{f}
&C \ar[d]^{g}
\\
B \ar@{-->}[r]_{q}
& D
}\\
\quad \In \dblcat{D}
`$
二重圏において、この形のフレームはニッチ〈niche〉と呼びます。
フレーム充填問題の事例: ニッチ充填問題
前節では、先に2-射〈二重射〉を与えて、その境界の一部としてフレーム -- より具体的にはニッチを提示しました。逆に、ニッチを与えて、そのニッチをフレーム(境界の一部)とする2-射を求める問題を考えましょう。これは、ニッチの充填問題〈filling problem〉です。
ニッチの充填問題は、次のような図式で示せます。
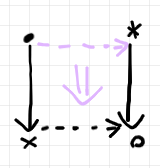
黒で描いてある部分が既知〈known〉の、あるいは所与〈given〉のフレームです。紫が未知〈unknown〉の部分です。方程式の定数と未知数と同様です。
図を90度回転しても内容は変わりません。プロ射を縦射〈vertical morphism〉、タイト射を横射〈horizontal morphism〉と呼ぶ習慣に合わせるなら、90度回転した以下の描き方がいいかも知れません。
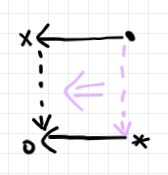
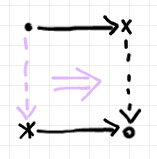
しかし、横方向は左から右がいいと感じる人が多そうですから、鏡映変換も施したほうが良さそうです(下図)。
最初のペースティング図のポアンカレ双対をとると、以下のストリング図になります。
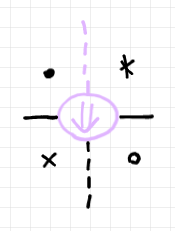
どのような図法・レイアウトで描こうが、二重圏におけるニッチの充填問題を記述していることに変わりはありません。
さて、所与フレーム〈given frame〉と未知項〈unknown〉を色を使って区別する代わりに、疑問符付きのラベルで未知項を表すことにしましょう。
$`\quad \xymatrix{
A \ar@{-->}[r]^{p?} \ar[d]_{f} \ar@{}[dr]|{\phi?\,\Downarrow\:}
&C \ar[d]^{g}
\\
B \ar@{-->}[r]_{q}
& D
}
`$
これをそのままテキストに写し取ると、ニッチの充填問題のテキスト表示が得られます。
$`\text{niche-fill}\\
\quad \phi? :: (f:A \to B)[p?\twoto q](g: C \to D) \In \dblcat{D}`$
疑問符で既知・未知を区別できるので、次のことを読み取れます。
- 二重圏 $`\dblcat{D}`$ の0-射〈対象〉 $`A,B,C,D`$ は所与〈既知〉である。
- 二重圏 $`\dblcat{D}`$ のタイト射 $`f, g`$ は所与〈既知〉である。
- 二重圏 $`\dblcat{D}`$ のプロ射 $`q`$ は所与〈既知〉である。
- 二重圏 $`\dblcat{D}`$ のプロ射 $`p?`$ は未知である。
- 二重圏 $`\dblcat{D}`$ の2-射 $`\phi?`$ は未知である。
つまり、上記の $`\text{niche-fill}`$ は、与えられた〈所与の | 既知の〉フレーム $`A, B, C, D, f, g, q`$ に対して、未知の部分 $`p?, \phi?`$ を求める問題です。
一般に、既知〈所与〉のフレームと未知項が指定された充填問題がフレーム充填問題〈frame filling problem〉です。未知項(今の例なら $`p?, \phi?`$)に代入可能な射の組み合わせを、フレーム充填問題の解〈solution〉、またはフィラー〈filler〉と呼びます。
フレーム充填問題のすべての解の集合を $`\mrm{Sol}(\hyp)`$ で表します。例えば、上記のニッチの充填問題の解の集合は $`\mrm{Sol}(\text{niche-fill})`$ です。解の集合が、単なる集合以上の構造を持つかも知れないことを暗示して $`\mrm{Sol}(\hyp)`$ を解空間〈solution space〉とも呼びます。
後でまた述べますが、解空間 $`\mrm{Sol}(\text{niche-fill})`$ が空でなく(解があり)、“最良の解”が存在するとき、その最良解の2-射部分を、デカルト2-射〈cartesian 2-morphism〉と呼びます。「最良」の意味は後で説明します。
フレーム充填問題としての右カン拡張
フレーム充填問題の事例をもうひとつ挙げておきます。以下の過去記事で扱った話題です。
2-圏 $`\cat{K}`$ において、次のような図式を考えます。
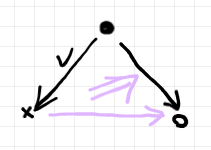
黒で描いた部分がフレーム(境界の一部)で、紫は未知項です。フレームの一部である0-射〈対象〉は、黒丸、バッテン、白丸です。フレーム内に2本の1-射があり、片方にはチェックマーク(v じゃありません)を付けています。このフレームの形状はスパン〈span〉と呼びます。
2-圏におけるスパン充填問題は、与えられたスパンに対して、1-射と2-射を付け足して〈充填して〉三角形に仕立てる問題です。
また、図のレイアウト変更を見てみましょう。最初のペースティング図を回転すると以下のようになります。
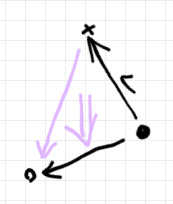
次は鏡映変換したものです。もちろん意味は変わりません。
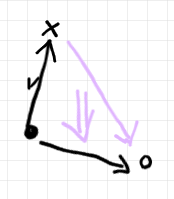
ポアンカレ双対をとってストリング図になります。このストリング図の描画方向は、1-射の結合の方向が左から右、2-射の縦結合の方向が上から下です。
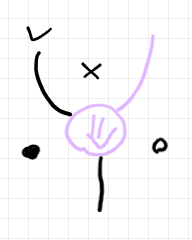
上のストリング図のポアンカレ双対を取れば、ペースティング図に戻りますが、レイアウトをより見やすいものにすれば次のようです。
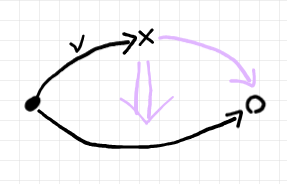
人により場合により、描画法やレイアウトは変わります。どう描いても意味は変わりません。描画法・レイアウト変更に対応するためのトレーニングについては、次の過去記事を参照してください。
さて、スパン充填問題を構成するすべての構成素にラベルを付けましょう。未知項のラベルには疑問符を後置します。
$`\quad \xymatrix@C+1pc{
{}
& D \ar@/^/[dr]^{s?}
& {}
\\
C \ar@/^/[ur]^{k} \ar@/_2pc/[rr]_{f} \ar@{}@/^/[rr]|{\tau?\; \Downarrow\:}
& {}
& E
}\\
\quad \In \cat{K}
`$
スパン充填問題をテキストで書き下すなら次のようです。
$`\text{span-fill}\\
\quad \tau? :: k * s? \twoto f : C \to E \In \cat{K}`$
アスタリスクは、2-圏の1-射の結合の図式順演算子記号です。各構成素のプロファイルを詳しく書くなら:
$`\text{span-fill}\\
\quad \tau? :: k * s? \twoto f : C \to E \In \cat{K}\\
\text{where}\\
\quad C, D, E \in |\cat{K}|\\
\quad k : C \to D \In \cat{K}\\
\quad f : C \to E \In \cat{K}\\
\quad s?: D \to E \In \cat{K}
`$
二重圏におけるスパン充填問題 $`\text{span-fill}`$ の解空間は $`\mrm{Sol}(\text{span-fill})`$ です。解空間 $`\mrm{Sol}(\text{span-fill})`$ が空でなく(解があり)、“最良の解”が存在するとき、その最良解の1-射部分を、$`f`$ の $`k`$ に沿った右カン拡張〈right Kan extension〉と呼びます。最良解の2-射部分には、決まった呼び名はありません。
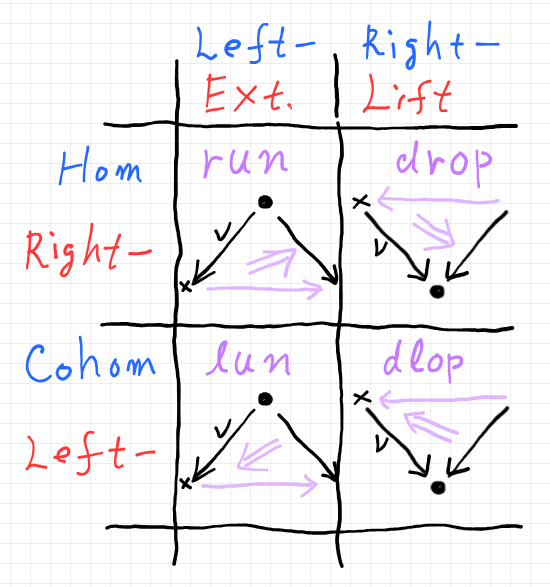
なお、別な形のスパン充填問題もあります。「カン拡張/カン持ち上げと上ホム対象/下ホム対象、充填三角形」で、コスパン充填問題と共に表にまとめたので再掲します。run, lun, drop, dlop は、スパン・コスパン充填問題の最良解の2-射部分に僕が付けた呼び名です。
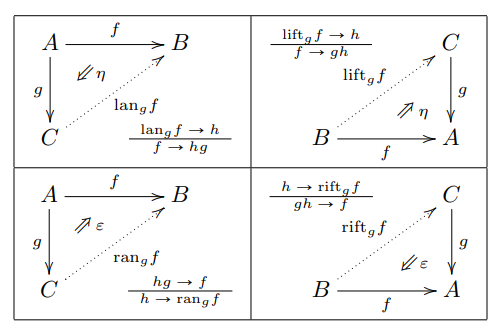
以下の論文内に、上と同様な、しかしずっときれいでシッカリした一覧表を見つけたので貼っておきます。
- [LL19-]
- Title: On the unicity of formal category theories
- Authors: Ivan Di Liberti, Fosco Loregian
- Submitted: 6 Jan 2019
- Pages: 38p
- URL: https://arxiv.org/abs/1901.01594
[/追記]
フレーム充填問題の最良の解
$`\text{something-fill}`$ を何らかのフレーム充填問題だとします。解空間 $`\mrm{Sol}(\text{something-fill})`$ が空集合のとき、与えられたフレームを埋めることはできません。つまり、「解なし」です。単一の解があるときはラッキーです。たくさんの解があるときは、そのなかから一番適切な解を選び出したい、ってことになります。
解空間 $`\mrm{Sol}(\text{something-fill})`$ が単なるノッペラボーの集合では、解の良さを比較できません。解空間には順序集合や圏の構造が必要となります。順序集合なら最小元または最大元を“最良”と思っていいでしょうし、圏なら終対象または始対象を“最良”と思っていいでしょう。
解空間に比較〈comparison〉の構造を入れるために使われる方法は、フレーム充填問題を、前層・余前層の表現・余表現問題に変換することです。フレーム充填問題の最良解は、前層・余前層の表現・余表現として与えられます。そして、前層・余前層の表現・余表現は、確かにとある圏*3の終対象・始対象になっています。
フレーム充填問題を、随伴系〈adjunction | adjoint system〉の構成問題に変換することもあります。これは結局、前層・余前層の表現・余表現問題に帰着されるので、やはり、とある圏の終対象・始対象を求めることになります。
より直接的で簡潔な最良解の記述は、一意因子分解〈unique factorization〉を用いる方法です。これは、一般の解と最良の解との隔たりを測る量を導入する方法です。隔たりを測る量とは、差(引き算の結果)や商(割り算の結果)のようなものです。
雰囲気的な説明をすると; 一般の解 $`\phi`$ と最良の解 $`\gamma`$ があるとき、その隔たりは $`\phi/\gamma`$ で計れるだろう、ということです。$`\phi' := \phi/\gamma`$ と置くと、$`\phi = \phi'\, \gamma`$ または $`\phi = \gamma\, \phi'`$ のような因子分解ができます。任意の解 $`\phi`$ に対して、一意的な因子分解ができることにより、$`\gamma`$ が最良であることの定義とします。
次節で、ニッチ充填問題の最良解とスパン充填問題の最良解を、一意因子分解により記述してみます。
デカルト2-射と右カン拡張1-射
二重圏 $`\dblcat{D}`$ のニッチ充填問題の一般の解〈フィラー〉を $`(p, \phi)`$ (疑問符は付いてない)とします。
$`\quad \xymatrix{
A \ar@{-->}[r]^{p} \ar[d]_{f} \ar@{}[dr]|{\phi\,\Downarrow\:}
&C \ar[d]^{g}
\\
B \ar@{-->}[r]_{q}
& D
} \\
\quad \In \dblcat{D}
`$
ニッチ充填問題の最良解を $`(w, \gamma)`$ とします。
$`\quad \xymatrix{
A \ar@{-->}[r]^{w} \ar[d]_{f} \ar@{}[dr]|{\gamma\,\Downarrow\:}
&C \ar[d]^{g}
\\
B \ar@{-->}[r]_{q}
& D
}\\
\quad \In \dblcat{D}
`$
$`(w, \gamma)`$ が最良であることは、任意の解 $`(p, \phi)`$ に対して、次のような因子分解が一意的に存在することです。
$`\quad \phi = \phi' ; \gamma`$
$`\phi'`$ が、$`\phi`$ と $`\gamma`$ を比較する量となっています。因子分解の等式を図式で書けば次のようです。
$`\quad \phi = \xymatrix{
A \ar@{-->}[r]^{p} \ar[d]_{\mrm{id}_A} \ar@{}[dr]|{\phi'\,\Downarrow\:}
& C \ar[d]^{\mrm{id}_C}
\\
A \ar@{-->}[r]^{w} \ar[d]_{f} \ar@{}[dr]|{\gamma\,\Downarrow\:}
&C \ar[d]^{g}
\\
B \ar@{-->}[r]_{q}
& D
}\\
\quad \In \dblcat{D}
`$
このような一意因子分解を可能にさせる解〈フィラー〉 $`(w, \gamma)`$ が、与えられたニッチ $`(f, g, q)`$ に対するデカルト2-射〈cartesian 2-morphism〉です。
次に、2-圏におけるスパン充填問題の最良解を考えましょう。2-圏 $`\cat{K}`$ のスパン充填問題の一般の解〈フィラー〉を $`(s, \tau)`$ (疑問符は付いてない)とします。
$`\quad \xymatrix@C+1pc{
{}
& D \ar@/^/[dr]^{s}
& {}
\\
C \ar@/^/[ur]^{k} \ar@/_2pc/[rr]_{f} \ar@{}@/^/[rr]|{\tau\; \Downarrow\:}
& {}
& E
}\\
\quad \In \cat{K}
`$
スパン充填問題の最良解を $`(g, \rho)`$ とします。
$`\quad \xymatrix@C+1pc{
{}
& D \ar@/^/[dr]^{g}
& {}
\\
C \ar@/^/[ur]^{k} \ar@/_2pc/[rr]_{f} \ar@{}@/^/[rr]|{\rho\; \Downarrow\:}
& {}
& E
}\\
\quad \In \cat{K}
`$
$`(g, \rho)`$ が最良であることは、任意の解 $`(s, \tau)`$ に対して、次のような因子分解が一意的に存在することです。
$`\quad \tau = (k * \tau') ; \rho`$
ここで、アスタリスクは1-射と2-射のあいだのヒゲ結合〈whiskering〉で、セミコロンは2-射の縦結合です。
$`\tau'`$ が、$`\tau`$ と $`\rho`$ を比較する量となっています。因子分解の等式を図式で書けば次のようです。
$`\quad \tau = \xymatrix@C+1pc{
{}
& D \ar@/_/[dr]_{g} \ar@/^1.5pc/[dr]^{s} \ar@{}@/^/[dr]|{\tau'\Downarrow\:}
& {}
\\
C \ar@/^/[ur]^{k} \ar@/_2pc/[rr]_{f} \ar@{}@/^/[rr]|{\rho\; \Downarrow\:}
& {}
& E
}\\
\quad \In \cat{K}
`$
このような一意因子分解を可能にさせる解〈フィラー〉 $`(g, \rho)`$ の1-射部分 $`g`$ が、与えられたスパン $`(k, f)`$ に対する右カン拡張1-射〈right Kan extension 1-morphism〉です。解の2-射 $`\rho`$ に名前が付いてないのは単に偶発的・歴史的事情です。
*1:くぼみの意味です。英語だと「ニーシ」に近い発音です。
*2:https://pixabay.com/vectors/water-rain-teardrop-liquid-drop-1560478/
*3:前層・余前層からグロタンディーク構成をして得られる“要素の圏”です。
