レナート・ベッチ/ロバート・ウォルターズ〈Renato Betti, Robert F.C. Walters〉のとある論文を眺めていて、カン拡張/カン持ち上げの記述で戸惑ってしまいました。右カン持ち上げだと記されていたペースティング図が間違っていて左カン持ち上げになっていたのが主な原因ですが、見慣れない記法が使われていたのも戸惑った理由のひとつです。
「カン拡張の左右: 混乱する原因がわかった!」で、左-右・二分法、正-余・二分法、拡張-持ち上げ・二分法が混在しているのでややこしい、という話をしましたが、ベッチ/ウォルターズは正-余・二分法と上-下・二分法を導入しており、さらにややこしい事になっています。
正-余・二分法によりホム対象とコホム対象を識別し、それを上-下・二分法で修飾することにより、上ホム対象/上コホム対象/下ホム対象/下コホム対象の4種類が生じます。さて、これらは他の用語法・記法では何に対応するのでしょうか?$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\hyp}{\text{-} }
%\newcommand{\o}[1]{\overline{#1} }
%\newcommand{\op}{\mathrm{op} }
`$
内容:
ベッチ/ウォルターズ論文
冒頭で言及したベッチ/ウォルターズの論文とは次です。
- [BW85]
- Title: Closed Bicategories and Variable Category Theory
- Authors: Renato Betti, Robert F.C. Walters
- Date: 1985, 2020
- Pages: 28p
- URL: http://www.tac.mta.ca/tac/reprints/articles/26/tr26.pdf
40年近く前の論文を2020年に復刻(?)したものです。豊穣圏〈enriched category〉の豊穣化ベース圏を、モノイド圏から双圏〈弱2-圏〉に一般化した圏類似構造(双圏ベースの豊穣圏〈{enriched}? category based on a bicategory〉)が出てきます。
双圏ベースの豊穣圏を考えるときに、ベース双圏に何らかの仮定を設けるでしょう。その仮定として、右カン拡張と右カン持ち上げの存在を要求しています。
現在の多数派の記法としては、右カン拡張は $`\mrm{Ran}_k f`$ 、右カン持ち上げは $`\mrm{Rift}_k f`$ です。ベッチ/ウォルターズは、右カン拡張と右カン持ち上げを内部ホム対象とみなしています。ニ種類の内部ホム対象があるので、適当な名前・記号を上付き・下付きで添えて区別します。上下添字に使う記号を黒丸とすると、右カン拡張が $`\mrm{hom}^\bullet(k, f)`$ 、右カン持ち上げが $`\mrm{hom}_\bullet(k, f)`$ となります。
右カン拡張/右カン持ち上げが内部ホム対象であるのは事実なのでよいのですが、二種の区別のために上-下・二分法を新たに導入しているので、「ウゲッ」とはなりました。
ベッチ/ウォルターズの論文の9ページのニ番目のペースティング図は間違っています。$`v \to w`$ となっていますが、$`w \to v`$ じゃないと辻褄が合いません。
テンソル・ホム随伴
$`\cat{C} = (\cat{C}, \otimes, I)`$ を、必ずしも対称とは限らないモノイド圏とします。$`T \in |\cat{C}|`$ を特定の対象として、$`T`$ を左から(モノイド積の意味で)掛け算する関手を左テンソリング関手〈left tensoring functor〉と呼びます。
$`\quad (T\otimes \hyp) : \cat{C} \to \cat{C} \in {\bf CAT}`$
左テンソリング関手の右随伴関手を左内部ホム関手〈left internal hom functor〉、あるいは短く左ホム関手〈left hom functor〉と呼び、$`\mrm{lhom}(T, \hyp)`$ と書きます*1。
$`\quad (T\otimes \hyp) \dashv \mrm{lhom}(T, \hyp)`$
この随伴系をテンソル・ホム随伴〈tensor-hom adjunction〉と呼びます。
随伴系から、(自然変換の意味で)自然なホムセット間同型が出てきます。次のようです。
$`\text{For }A, B \in |\cat{C}|\\
\quad \cat{C}(T\otimes B, A) \cong \cat{C}(B, \mrm{lhom}(T, A)) \In {\bf Set}`$
左を右に変えると、右テンソリング関手〈right tensoring functor〉、右内部ホム関手〈right internal hom functor〉(右ホム関手〈right hom functor〉)が定義できます。
$`\quad (\hyp \otimes T ) : \cat{C} \to \cat{C} \in {\bf CAT}`$
$`\quad (\hyp \otimes T) \dashv \mrm{rhom}(T, \hyp)`$
$`\text{For }A, B \in |\cat{C}|\\
\quad \cat{C}( B \otimes T, A) \cong \cat{C}(B, \mrm{rhom}(T, A)) \In {\bf Set}`$
左内部ホム関手/右内部ホム関手の値である $`\mrm{lhom}(T, A),\; \mrm{rhom}(T, A)`$ をそれぞれ、左内部ホム対象/右内部ホム対象〈left/right internal hom object〉、あるいは短く左ホム対象/右ホム対象〈left/right hom object〉と呼びます。
モノイド圏が対称なら、左右を神経質に区別する必要はありませんが、非対称なモノイド圏では左右の区別が必要です。
カリー化/反カリー化と指数対象
内部ホム対象を指数対象〈exponential object〉とも呼びます。モノイド圏がデカルト・モノイド圏(したがって対称)のときに、「指数対象」と呼ぶことが多いですが、「内部ホム対象」と「指数対象」を同義語として使ってもいいと思います。以下、同義語として使います。
モノイド圏が非対称なら左指数対象と右指数対象の区別が必要です(対称であっても区別したほうがスッキリします)。指数対象を累乗の記法で書くとして次のように区別します。
$`\text{For }A, B \in |\cat{C}|\\
\quad \cat{C}(T\otimes B, A) \cong \cat{C}(B, {^T\!\! A}) \In {\bf Set}\\
\quad \cat{C}( B \otimes T, A) \cong \cat{C}(B, A^T ) \In {\bf Set}`$
左指数が左肩、右指数が右肩なので覚えやすいですね。
前節のテンソル・ホム随伴と、上記の積・指数・随伴〈product-exponential adjunction〉は同じことです。強いてニュアンスを言えば、積・指数はデカルト閉圏の雰囲気がただよいます。
積・指数・随伴の、ホムセット同型を与える写像を、カリー化〈currying〉と反カリー化〈uncurrying〉と呼びます。
$`\quad \mrm{LCurry}_{T,B, A} : \cat{C}(T\otimes B, A) \to \cat{C}(B, {^T\!\! A})\\
\quad \mrm{LUncurry}_{T,B, A} : \cat{C}(B, {^T\!\! A}) \to \cat{C}(T\otimes B, A)\\
\quad \mrm{RCurry}_{T,B, A} : \cat{C}(B \otimes T , A) \to \cat{C}(B, A^T)\\
\quad \mrm{RUncurry}_{T,B, A} : \cat{C}(B, A^T) \to \cat{C}(B \otimes T, A)
`$
カリー化/反カリー化は、もともとはラムダ計算の言葉ですが、一般的なテンソル・ホム随伴の状況でも使ってよいと思います。僕は、テンソル・ホム随伴と積・指数・随伴を特に区別してません。
内部コホム対象=余指数対象
テンソル・ホム随伴では、左右のテンソリング関手に対して、その右随伴として左右のホム関手を定義しました。右随伴ではなくて左随伴を考えると、左右のコホム関手になります。
左内部コホム関手〈right internal cohom functor〉(左ホム関手〈right hom functor〉)は次のようです。
$`\quad \mrm{lcohom}(T, \hyp) \dashv (T \otimes \hyp)`$
$`\text{For }A, B \in |\cat{C}|\\
\quad \cat{C}(\mrm{lcohom}(T, A), B ) \cong \cat{C}( A , T \otimes B) \In {\bf Set}`$
左を右に変えると、右内部コホム関手〈right internal cohom functor〉(右コホム関手〈right cohom functor〉)が定義できます。
$`\quad \mrm{rcohom}(T, \hyp) \dashv ( \hyp \otimes T )`$
$`\text{For }A, B \in |\cat{C}|\\
\quad \cat{C}(\mrm{rcohom}(T, A), B ) \cong \cat{C}( A, B \otimes T) \In {\bf Set}`$
左内部コホム関手/右内部コホム関手の値である $`\mrm{lcohom}(T, A),\; \mrm{rcohom}(T, A)`$ をそれぞれ、左内部コホム対象/右内部コホム対象〈left/right internal cohom object〉、あるいは短く左コホム対象/右コホム対象〈left/right cohom object〉と呼びます。
さて、ベッチ/ウォルターズの二分法は、左右ではなくて上下です。右ホム関手/対象が上ホム関手/対象で、左ホム関手/対象が下ホム関手/対象です。なんでそういう対応なのか? に何の理由もないでしょう。「そう決めたからそうなんだ」としか言いようがありません。上下の区別は、丸印を上下に添えることにします。
次は同義語になります。
- 左ホム対象 = 左指数対象 = 下ホム対象 :
$`\quad \mrm{lhom}(T, A) = {^T\!\! A} = \mrm{hom}_\bullet(T, A)`$ - 左コホム対象 = 左余指数対象 = 下コホム対象 :
$`\quad \mrm{lcohom}(T, A) = {_T\! A} = \mrm{cohom}_\bullet(T, A)`$ - 右ホム対象 = 右指数対象 = 上ホム対象 :
$`\quad \mrm{rhom}(T, A) = A^T = \mrm{hom}^\bullet(T, A)`$ - 右コホム対象 = 右余指数対象 = 上コホム対象 :
$`\quad \mrm{rcohom}(T, A) = A_T = \mrm{cohom}^\bullet(T, A)`$
上-下・二分法が使われることは稀なので、別に覚える必要はありません。が、左-右・二分法以外が使われるケースも在ることは知っておいたほうがいいでしょう。
カン拡張とカン持ち上げ
左右の代わりに上下を使うときは、「左←→下」「右←→上」と置き換えるだけなので、言い方の違いで済みます。しかし、カン拡張/カン持ち上げの場合は、二分法の分類軸の取り方が食い違うので面倒です。それについては「カン拡張の左右: 混乱する原因がわかった!」に書いています。
カン拡張/カン持ち上げも追加した同義語の対応だけ示しておきます。下の図は「カン拡張の左右: 混乱する原因がわかった!」からの再掲です。
- 右カン拡張 = 左ホム対象 = 左指数対象 = 下ホム対象 :
$`\quad \mrm{Ran}_T A = \mrm{lhom}(T, A) = {^T\!\! A} = \mrm{hom}_\bullet(T, A)`$ - 左カン拡張 = 左コホム対象 = 左余指数対象 = 下コホム対象 :
$`\quad \mrm{Lan}_T A = \mrm{lcohom}(T, A) = {_T\! A} = \mrm{cohom}_\bullet(T, A)`$ - 右カン持ち上げ = 右ホム対象 = 右指数対象 = 上ホム対象 :
$`\quad \mrm{Rift}_T A = \mrm{rhom}(T, A) = A^T = \mrm{hom}^\bullet(T, A)`$ - 左カン持ち上げ = 右コホム対象 = 右余指数対象 = 上コホム対象 :
$`\quad \mrm{Lift}_T A = \mrm{rcohom}(T, A) = A_T = \mrm{cohom}^\bullet(T, A)`$
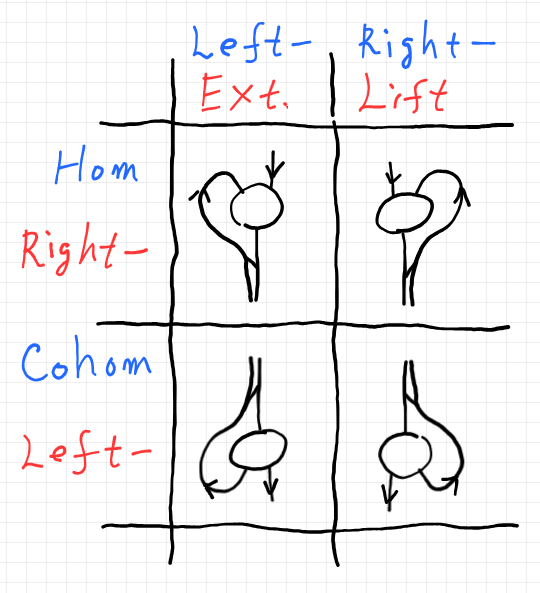
カン拡張/カン持ち上げは、2-圏における概念ですが、モノイド圏は特殊な2-圏(単対象の2-圏)なので、カン拡張/カン持ち上げとホム対象/コホム対象は同じことです。ただし、使っている二分法が「拡張-持ち上げ・二分法 + 左-右・二分法」と「正-余・二分法 + 左-右・二分法」であり、二分法の分類軸の取り方が食い違いがあり、対応が取りにくくなっています。
いまさらどうにもなりませんが、共通した整合的ネーミングと記法で記述すればスッキリ・ハッキリしていたでしょう。なんでこうなった?
スパン/コスパンの充填としての拡張/持ち上げ
$`\cat{K}`$ を2-圏として、$`\cat{K}`$ のなかでスパンを考えることができます。
$`\quad\xymatrix{
{}
&\bullet \ar[dl]_{\checkmark} \ar[dr]
&{}
\\
{\mathsf x}
&{}
&{}
}\\
\quad \In \cat{K}
`$
スパンを構成する対象を、ボディ〈body〉(またはヘッド〈head〉)と足〈foot〉と呼びます。上の図で、ボディは黒丸にしています。スパンを構成する1-射は脚〈leg〉です。
スパンは2本の脚を持ちますが、どちらかを特定したとき、特定した脚を軸脚〈pivot leg〉と呼ぶことにします。左脚とかにしないのは、左右での識別にはもうコリゴリだからです。上の図で、軸脚にはチェックマークを付けています。
三角形は内部を含む2次元の図形で、三辺形は直線だけでできた1次元の図形のことだとします。スパンの足達を結ぶ1-射と、三辺形を埋めて三角形にするための2-射の組を、スパンの充填〈filler〉と呼ぶことにします。充填に使う1次元の辺は充填1-射〈filler 1-morphism〉、二次元の領域は充填2-射〈filler 2-morphism〉とします。
コスパンはスパンの双対で、射が足からボディに向かいます。コスパンでは、足からボディに向かう射は余脚〈coleg〉と呼ぶことにします。コスパンの2本の余脚のうち、どちらかを特定したとき、特定した余脚を軸余脚〈pivot coleg〉と呼ぶことにします。
カン拡張/カン持ち上げは、軸が指定されたスパン/コスパンを充填して三角形にすることです。充填1-射の向きと充填2-射の向きにより、左カン拡張/右カン拡張/左カン持ち上げ/右カン持ち上げの違いが生じます。以下のようです。
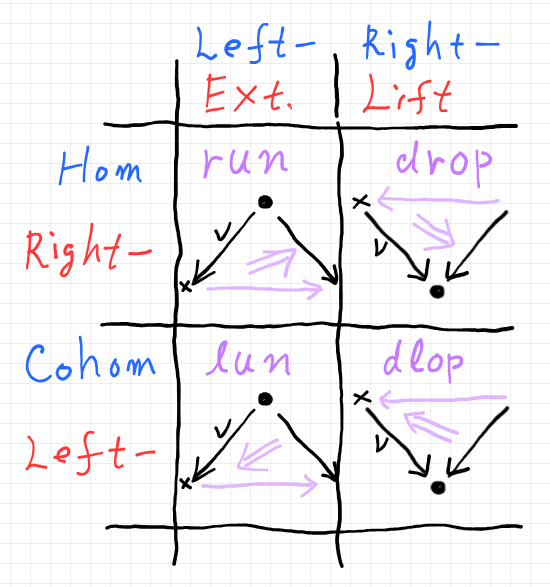
黒がスパン/コスパン、紫が充填1-射/充填2-射です。run, lun, drop, dlop は、充填2-射の名前です。一般的ではありませんが、僕はこう呼んでいます。充填1-射には色々な呼び名や記法があります(あり過ぎます)が、充填2-射には呼び名・記法がなくて困ります。
軸として指定する1-射を $`k`$ 、もう一方の脚/余脚を $`f`$ とすると、拡張の場合は「$`f`$ を $`k`$ に沿って〈along〉拡張する」と言い、持ち上げの場合は「$`f`$ を $`k`$ を通して〈through〉持ち上げる」と言うようです。
食い違った分類軸やら言い回しのしきたりやら珍しい方言やらナニヤラで、カオスなのですが、いかんともしがたいですわ。
*1:ホム関手だと、外部ホム関手(通常のホム関手)と区別が付かないので、ホミング関手〈homing functor〉のほうがいいかも知れません。