「木と林(有向グラフ)」より:
頂点〈ノード〉の高さと林/ツリーの高さは、関連してますが別な概念なので混同しないようにしましょう。
別な概念は別な名前を付けたほうがいいですね。$`\newcommand{\mrm}[1]{ \mathrm{#1} }\newcommand{\cat}[1]{\mathcal{#1}}`$
以上に定義した $`\mrm{Path}_* (\cat{S})`$ の形(アスタリスクはワイルドカード)をした圏を、圏 $`\cat{S}`$ のパスの圏〈category of paths〉と呼びます。「パスの圏」は、グラフから自由生成された圏の意味もあるので、用語のコンフリクト〈衝突〉ですが、他の呼び名が思いつきません。
この用語のコンフリクトはマズい気がするので、他の呼び名をひねり出すことにします。
混乱が起きないように用語・概念を整理すると共に、レベル付き林の圏を導入します。そして、一般的な圏論的構成法として“レベル付き林構成”を示唆します。$`\newcommand{\hyp}{\text{-} }
\newcommand{\In}{\text{ in }}
\newcommand{\F}[1]{ {{#1}^{-1}} } % fiber
\newcommand{\obj}[1]{ {{#1}\!\downarrow} }
\newcommand{\dimU}[2]{ {{#1}\!\updownarrow^{#2}} }
`$
内容:
木〈ツリー〉/林のレベル関数
有限無向グラフの場合、ルート〈根〉を持たないツリーという概念があります。下の図は、ルートを持たない有限無向ツリーの例です。
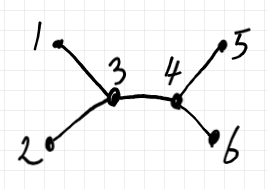
有限無向ツリーのひとつの頂点を“ルート”として選ぶとルート付きツリー〈rooted tree〉になります。頂点 1 をルートに選んだ場合と頂点 3 をルートに選んだ場合の図は以下のようです。
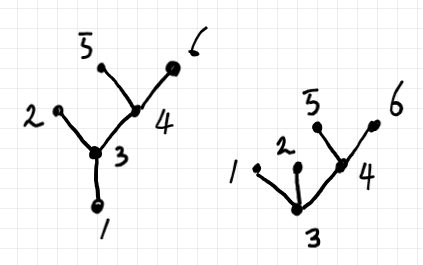
「木と林(有向グラフ)」で、頂点〈ノード〉の高さと呼んでいた値/関数を、レベル〈level〉に変更します。レベルは、ルートからリーフの方向に増加するとします。ルートのレベルは 0 です。
上の図の左のルート付きツリーのレベルは次のようです。
| 頂点番号 | 頂点のレベル値 |
|---|---|
| 1 | 0 |
| 2 | 2 |
| 3 | 1 |
| 4 | 2 |
| 5 | 3 |
| 6 | 3 |
上の図の右のルート付きツリーのレベルは次のようです。
| 頂点番号 | 頂点のレベル値 |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 0 |
| 4 | 1 |
| 5 | 2 |
| 6 | 2 |
レベル関数を備えたツリーをレベル付きツリー〈leveled tree〉と呼ぶことにします。幾つかのレベル付きツリーの直和はレベル付き林〈leveled forest〉です。レベル付き林のなかで、連結成分がひとつだけのものがレベル付きツリーです。
以上のように定義したレベル付き林は無向グラフですが、leaf-to-rootな向き〈leaf-to-root direction〉か、またはroot-to-leafな向き〈root-to-leaf direction〉な向き(「木と林(有向グラフ) その2」参照)で向き付けして有向グラフになります。ここでは、leaf-to-rootな向き(ボトムアップな向き〈bottom-up direction〉)を採用します。
無向グラフに向き付けすれば有向グラフなので、最初から有向グラフとしてレベル付き林を定義してもかまいません。有向グラフとしてのレベル付き林の定義は「木と林(有向グラフ)// 特殊なグラフ」にあります。有限性を仮定してません。林に二種類の向き付けがあることは「木と林(有向グラフ) その2」で説明しています。
レベル付き林を、記号の乱用で次のように書くことにします。
$`\quad F = (F, \mrm{level}_F)`$
$`\mrm{level}_F`$ はレベル関数です。
$`\quad \mrm{level}_F : \mrm{Vert}(F) \to {\bf N} \In {\bf Set}`$
グラフの準同型射〈グラフ射〉で、レベルを保つものをレベル付き林のあいだの射とします。レベル付き林を対象、レベルを保つグラフ射を射とする圏を構成できるので、それを次のように書きます。
$`\quad {\bf LvForest} \; \in |{\bf CAT}|`$
圏 $`{\bf LvForest}`$ の対象として、空グラフは除外しておきます。空グラフを使う機会がなさそうで、むしろ邪魔になるので。
圏 $`{\bf LvForest}`$ は、「木と林(有向グラフ) その2」で $`{\bf Forest}^\mrm{hp}`$ と書いた圏と、空グラフを除外した以外の差はありません。「頂点の高さ」を「頂点のレベル」に変更して、レベル関数を構造の一部に組み込んだことになります。
レベル付き林 $`F\in |{\bf LvForest}|`$ に対して、頂点のレベルの最大値を、レベル付き林の高さ〈height〉と呼びます。林が有限とは仮定してないので、自然数としての最大値が存在しないかも知れません。そのときは高さ $`\infty`$ とします。「木と林(有向グラフ) その2」に書いたとおり、レベル付き林の高さは関手になります。
$`\quad \mrm{Height} : {\bf LvForest} \to \mrm{COS}({\bf N}_\infty) \In {\bf CAT}`$
空グラフを除外したので、高さの値として $`-\infty`$ は不要になりました。$`\mrm{COS}`$ は Category from Ordered Set でした。
ところで、$`\mrm{COS}`$ のような略称は、憶えにくいので、「スケマティック系のために: 雑多な予備知識」で述べたコアージョン記法を使ったほうが良さそうです。
$`\quad \mrm{Height} : {\bf LvForest} \to ({\bf N}_\infty \text{ as }{\bf Cat}) \In {\bf CAT}`$
ここで、$`({\bf N}_\infty \text{ as }{\bf Cat})`$ は、小さい圏達の2-圏 $`{\bf Cat}`$ の対象とみなした $`{\bf N}_\infty`$ のことです。$`{\bf N}_\infty`$ が順序集合であることは前提して、順序集合から圏を作る手順も既知とすれば、$`\text{ as }{\bf Cat}`$ の意味はわかるでしょう。
レベル付き林のネクスト関数
$`F \in |{\bf LvForest}|`$ とします。$`F`$ の頂点〈ノード〉達は、レベルにより分類できます。
$`\text{For }k \in {\bf N}\\
\quad \mrm{Vert}_k(F) := \{v \in \mrm{Vert}(F)\mid \mrm{level}_F(v) = k \}`$
特に、レベル 0 の頂点達がルート集合を形成します。
$`\quad \mrm{Root}(F) = \mrm{Vert}_0(F)`$
空グラフを除いたので、任意のレベル付き林に対して $`\mrm{Root}(F) \ne \emptyset`$ です。ルート以外の頂点達の集合は次のように書きます。
$`\quad \mrm{Vert}_{\ge 1}(F)`$
$`\mrm{Vert}_{\ge 1}(F)`$ は空である可能性があります。
有向グラフとしての林 $`F`$ の特徴として、次が成立します。
- $`v\in \mrm{Vert}(F)`$ がルートでないなら、$`\mrm{Out}(F, v)`$ はただひとつの辺からなる。
ここで、$`\mrm{Out}(F, v)`$ の定義(「木と林(有向グラフ)// 特殊なグラフ」より再掲)は:
$`\quad \mrm{Out}(G, v) := \{e\in \mrm{Edge}(G) : \mrm{src}(e) = v\}`$
ルートではない頂点〈ノード〉から出る辺が一本しかないので、その辺の終点〈ターゲット頂点〉も唯一です。このことを利用して、$`\mrm{next}_F`$ という関数〈写像〉を次のように定義します。
$`\text{For }v\in \mrm{Vert}_{\ge 1}(F)\\
\quad \mrm{next}_F(v) := \mrm{trg}(e_v) \;\in \mrm{Vert}(F)\\
\text{Where }\\
\quad e_v \in \mrm{Out}(F, v)
`$
ルート頂点に関しては、出る辺が存在しないので $`\mrm{next}_F`$ の値は定義できません。$`\mrm{next}_F`$ は次のような関数です。
$`\quad \mrm{next}_F : \mrm{Vert}(F)_{\ge 1} \to \mrm{Vert}(F) \In {\bf Set}`$
$`\mrm{next}_F`$ を、レベル付き林 $`F`$ のネクスト関数〈next function〉と呼ぶことにします。
集合と写像によるレベル付き林の定義
前節のネクスト関数があれば、レベル付き林の辺は再現できます。つまり、辺という概念を使わなくてもレベル付き林は定義できます。
$`V`$ は(有限とは限らない)空でない集合として、$`V`$ の部分集合 $`V'`$ と次の2つの関数を考えます。
$`\quad f : V \to {\bf N} \In {\bf Set}\\
\quad g : V' \to V \In {\bf Set}
`$
次の定義をします。($`f^{-1}(\hyp)`$ は要素の逆像。)
$`\text{For }k \in {\bf N}\\
\quad V_k := f^{-1}(k)`$
次の条件を付けます。
- $`V_0 \ne \emptyset`$
- $`V' = V \setminus V_0`$
- $`g(V_{k + 1}) \subseteq V_k`$
$`V'`$ は $`V`$ と $`f`$ から計算できるので明示しないことにして、上記の条件を満たす3つ組 $`(V, f, g)`$ を考えます。$`(V, f, g)`$ があれば、そこから次のようなレベル付き林を構成できることはわかるでしょう。
- $`\mrm{Vert}(F) = V`$
- $`\mrm{level}_F = f`$
- $`\mrm{next}_F = g`$
辺やその始点・終点という概念を使わずに、3つ組 $`(\mrm{Vert}(F), \mrm{level}_F, \mrm{next}_F)`$ (上記条件を満たす)をレベル付き林だと定義してかまいません。
もうひとつ別な形の定義を考えます。$`(V, f, g)`$ のレベル関数 $`f`$ の代わりに、集合 $`V`$ が次のように直和分割されているとします。
$`\quad V = V_0 + V_1 + V_2 + \cdots`$
ここでの直和はタグ付き合併ではなくて、単なる合併だが共通部分はないと解釈します。$`V_0 \ne \emptyset`$ は仮定しますが、他の直和成分〈summand〉は空でもかまいません。この直和分割とレベル関数は同じことなので、レベル関数の代わりに直和分割が使えます。
ネクスト関数 $`g`$ は次の関数になります。
$`\quad g : (V_1 + V_2 + \cdots) \to V \In {\bf Set}`$
関数 $`g`$ を次のように細切れにします。$`\hyp|_{A}^{B}`$ は、写像の域と余域の部分集合への制限です。
$`\text{For } n\in {\bf N}_{\ge 1}\\
\quad g_n := g|_{V_n}^{V{n - 1}} \;: V_n \to V_{n - 1} \In {\bf Set}
`$
このような細切れが定義できるためには、条件 $`g(V_{n}) \subseteq V_{n -1}`$ が必要です。細切れにした $`g_n`$ 達は次の図式として書けます。
$`\quad \cdots \to V_n \overset{g_n}{\to} V_{n - 1} \to \cdots \to V_1 \overset{g_1}{\to} V_0
\;\In {\bf Set}
`$
直和成分 $`V_k`$ が空集合なら、$`V_{k + 1}`$ も空集合で、$`k`$ より大きい番号ではずっと空集合が続きます。もし、空集合が出現したら、空集合は書かないことにします。$`V_0`$ は(仮定した条件から)空集合ではないので、もっとも短い記述は次です。
$`\quad V_0 \;\In {\bf Set}\\
\text{Or}\\
\quad V_0 \;\in |{\bf Set}|
`$
次は $`V_1 \ne \emptyset`$ で、その他は空集合の場合です。
$`\quad V_1 \overset{g_1}{\to} V_0 \;\In {\bf Set}`$
結局、有限個の写像の系列 $`(g_k)_{1 \lt k \le n}`$ 、または無限個の写像の系列 $`(g_k)_{n\in {\bf N}_{\ge 1}}`$ によりレベル付き林を記述できます。空集合は取り除く約束なので、写像 $`g_k`$ の域・余域は空ではありません。
域・余域が空ではない写像達の有限または無限の系列があれば、そこからレベル付き林を再現できます。よって、写像達の系列をレベル付き林だと定義してかまいません。
もう少しハッキリと言うと; 写像達の系列が有限の系列の場合は、レベル付き林を次のように記述できます。
- $`n \in {\bf N}`$
- $`0 \le k \le n`$ に対して、$`V_k \in |{\bf Set}|`$ 、$`V_k \ne \emptyset`$
- $`1 \le k \le n`$ に対して、$`g_k : V_k \to V_{k - 1} \In {\bf Set}`$
無限の系列の場合は、レベル付き林を次のように記述できます。
- $`k \in {\bf N}`$ に対して、$`V_k \in |{\bf Set}|`$ 、$`V_k \ne \emptyset`$
- $`k \in {\bf N}_{\ge 1}`$ に対して、$`g_k : V_k \to V_{k - 1} \In {\bf Set}`$
レベル付き林の高さ〈height〉は、系列の長さで定義します。有限の場合なら $`n`$ 、無限の場合なら $`\infty`$ とします。写像達の系列として定義されたレベル付き林を $`F, G`$ などで表し、その高さを $`\mrm{Height}(F)`$ などとします。$`\mrm{Vert}(F), \mrm{Vert}_k(F)`$ などの記法も使います(定義は明らかでしょう)。
2つのレベル付き林 $`F, G`$ のあいだの準同型射は、$`\mrm{Height}(F) \le \mrm{Height}(G)`$ のときだけ定義できます。高さ $`n = \mrm{Height}(F)`$ が有限のときは、$`F`$ から $`G`$ への準同型射は $`n`$ 個の写像で定義できます。
$`\text{For }0 \le k \le n\\
\quad \varphi_k : \mrm{Vert}_k(F) \to \mrm{Vert}_k(G) \In {\bf Set}
`$
$`1 \le k \le n`$ に対して、次の図式が可換になることを要求します。無名の矢印は、レベル付き林のネクスト関数(の細切れ)です。
$`\require{AMScd}
\quad \begin{CD}
\mrm{Vert}_k(F) @>{\varphi_k}>> \mrm{Vert}_k(G)\\
@VVV @VVV\\
\mrm{Vert}_{k-1}(F) @>{\varphi_{k -1}}>> \mrm{Vert}_{k -1}(G)
\end{CD}\\
\quad \text{commutative }\In {\bf SET}
`$
これで、写像達の系列としてのレベル付き林とそのあいだの準同型射が定義できたので、それに基づいて圏を構成できます(確認事項はありますが)。定義を変えても、できあがる圏には差がない(圏同値となる)ので、別な名前は使わずに、圏 $`{\bf LvForest}`$ とします。この圏の対象が、有向グラフに条件を付けて定義されようが、写像達の系列として定義されようが、それは気にしないで扱う、ということです。
レベル付き林構成
前節の、写像達の系列としてのレベル付き林の定義では、集合圏特有の概念は“ほぼ”出てきてません。一般の圏のなかで、射達の系列としてのレベル付き林が定義可能でしょう。「ほぼ」の理由は、レベル付き林の高さをうまく定義するために、「空ではない集合」という条件を付けているので、空集合を一般的条件に置き換える必要があります。
空集合は集合圏の始対象なので、「空ではない」を「始対象ではない」にすればいいでしょう。用途によっては、特に条件を付ける必要がないかも知れません。あるいは、もっと強い条件が必要な場合もあるでしょう。いずれにしても、適切な対象達を並べて、そのあいだの射達の系列を考えれば、レベル付き林は定義できます。レベル付き林のあいだの射の定義では、可換図式で条件を付けています。この定義はどんな圏でも通用します。
以上より、一般的な圏 $`\cat{C}`$ から、$`\cat{C}`$ におけるレベル付き林の圏 $`\mrm{LvForest}(\cat{C})`$ を構成できます。このレベル付き林構成〈leveled forest construction〉の定義には、Diag構成(「Diag構成: 圏論的構成法の包括的フレームワークとして」参照)の仕掛け〈マシナリー〉を使うと良さそうです。が、今日のところはだいたいの筋道だけでいいとします。