ラムダ計算の自然性とお絵描き - 檜山正幸のキマイラ飼育記 (はてなBlog)

タイトルの「自然性」は、国語辞書的な意味ではなくて、圏論の意味での自然性です。何が自然なのかというと、ラムダ計算の中核であるカリー化が自然だということです。なので、正確に言えば：

ラムダ計算の中核であるカリー化は、圏論的な意味で自然である。

このことを、お絵描き（ストリング図による描画）を混じえて説明します。

内容：

モノイド閉圏
カリー化と反カリー化
カリー化に関するタイトニング／スライディング
自然性をまとめてみると

モノイド閉圏

ラムダ計算のセマンティクス〈モデル〉は、通常はデカルト閉圏〈Cartesian closed category〉により与えられます。しかし、もう少し一般化してモノイド閉圏〈monoidal closed category | 閉モノイド圏 | closed monoidal category〉でもラムダ計算の解釈はできます。

モノイド閉圏は、モノイド構造と整合した閉構造を持つモノイド圏です。モノイド積を持たない閉圏〈closed category〉という概念もあり、含意しか持たない論理のセマンティクスに使われたりします。ラムダ計算もモノイド積無しの閉圏で解釈するテがありますが（ときに望ましいかも）、モノイド積がないとだいぶ扱いにくく苦労するので、（型付きの）ラムダ計算の話ではモノイド積を使ってもいいと思います

モノイド閉圏には、モノイド積以外に指数〈exponential〉とか内部ホム〈internal hom〉と呼ばれる演算が要求されます。指数／内部ホムは、Y^A, hom(A, Y), [A, Y] などと書かれます。デカルト閉圏のときは「指数」、一般的な文脈では「内部ホム」と呼ぶ習慣のようですが、こういう区別に拘ってもしょうもないので同義語扱い「指数＝内部ホム」でいいでしょう。指数／内部ホムに関しては：

モノイド積と指数を絵に描くときは、次のようにします。

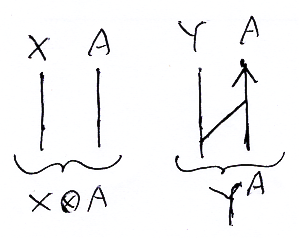
圏の対象がワイヤー〈ストリング〉で、ワイヤーの並置（単に横に並べる）はモノイド積で、ワイヤーのあいだに斜め線を引くと指数です。指数の右のワイヤーは逆向き（下から上）に走ると考えると都合がいいです。

なお、ここでの描画方向は、射の結合方向が上から下、モノイド積の方向が左から右です。旗で示せば：

カリー化と反カリー化

モノイド閉圏Cには、モノイド積と指数が備わっているのでした。これらの演算は、二項関手〈双関手〉になります。

モノイド積二項関手 (- $\otimes$ -):C×C→C
指数二項関手 [-, -]:C^op×C→C

モノイド積は共変-共変の二項関手、指数は反変-共変の二項関手です。ただし、どっちの変数が反変になるかは書き方に依存します*1。例えば、指数形式 X^A を中置演算子記号で X^A と書くと約束すると、

(-^-):C×C^op→C

です。この記事では、X^A = [A, X] とAを左に書くので、第一変数〈左変数〉に関して反変です。

Cがモノイド閉圏であるためには、次の条件が必要です。

任意の対象 A∈|C| が定義する関手 (- $\otimes$ A) と [A, -] は随伴ペアになる。

随伴を正確に記述するために、随伴系を「随伴に関する注意事項」に従って書くとすれば、次の随伴系〈adjunction | adjoint system〉があります。

(η, ε: (- $\otimes$ A) -| [A, -], (- $\otimes$ A):C→C)

この随伴系を、指数随伴系〈exponential adjunction〉とかテンソル・ホム随伴系〈tensor-hom adjunction〉と呼びます。「テンソル・ホム」の由来は；テンソル積はモノイド積と同義に使われることがあり、ホムは内部ホム、つまり指数です。「テンソル・ホム」は「モノイド積と指数のあいだの」という形容詞です。

Cの対象 X, Y を選んで、指数随伴系が導くホムセット間同型を書けば：

C(X $\otimes$ A, Y) $\cong$ C(X, [A, Y])

この同型を与える左から右方向の写像をカリー化〈currying〉と呼び、Λで書くことにします。

Λ:C(X $\otimes$ A, Y)→C(X, [A, Y])

随伴系の定義より、Λには逆写像が存在します。Λ^-1を反カリー化〈uncurrying〉と呼びます*2。

カリー化写像Λは、構文的なラムダ抽象操作に対応します。反カリー化写像Λ^-1に対応する構文的な操作はラムダ反抽象とでも言えばいいのでしょうか？（呼び名は知らない）

通常の（デカルト閉圏における）ラムダ計算では、カリー化（＝ラムダ抽象）は、「多変数関数の変数を減らして高階関数にする」ことだと説明されます。キャッチフレーズとしては、「カリー化は高階関数化」だと言っていいでしょう。となると、反カリー化（＝ラムダ反抽象）は低階関数化だと言えるでしょう。「低階関数化」って聞いたことないけど。

カリー化は、多変数関数の変数を減らして、より高階な関数にする。（高階関数化）
反カリー化は、高階関数の変数を増やして、より低階な関数にする。（低階関数化）

ツジツマはあってるよね。

[補足]
fのカリー化 Λ(f) を f^∧, f^∩ などの上付きオペレーター記号で書くことがあります。Λ, λ, ^, ∧, ∩ は形状が似ているので連想が働きます。それとは別な上付きオペレーターで、♭, # を使う流儀があります。音楽記法〈music notation〉と呼ばれ、互いに逆（または互いに双対）なオペレーターをフラットとシャープで表します。

カリー化／反カリー化でも音楽記法を使うことがあります。すぐ上の説明のごとく、カリー化が高階化なので半音上げ（高くする）でシャープを使って欲しいですね。しかし残念ながら、Λ(f) = f^♭ と書くのが習慣です。ナンダヨ、モー。
[/補足]

カリー化に関するタイトニング／スライディング

一般的な随伴系を (η, ε : F -| G, F:C→D) とすると、そのカリー化（転置）同型写像は次のようになります。

ψ^X_Y : D(F(X), Y)→C(X, G(Y))

ホムセット間同型写像は、対象 X∈C, Y∈D ごとに決まるので ψ^X_Y と書きました。添字 X, Y を上下に振り分けたのは後の記法と合わせるためです。

随伴系の条件として、ホムセット間同型の族が存在するだけでなくて、「X, Y に関して自然である」という条件が付きます。この条件は分かりにくいし、明示的な解説も少ないです。「圏論の随伴をちゃんと抑えよう：お絵描き完全解説 // 転置と反転置の自然性」でかなり詳しく書いているので興味があれば参照してください。

ここでは、指数随伴系〈テンソル・ホム随伴系〉に関しての自然性を扱います。指数随伴系のカリー化同型写像を添字付きで書くと：

Λ^X,A_Y : C(X $\otimes$ A, Y)→C(X, [A, Y])

Λ^X,A_Y には3つの添字（X, A, Y）がありますが、これら3つの添字（対象変数）に関する自然性が要求されます。これから、その自然性を等式と絵で表すことにします。

以下で出てくる対象と射は次です。縦に書いているのは絵に合わせてです。

$\require{AMScd} \begin{CD} X' @. A' \\ @V{v}VV @VV{p}V \\ X @. A \\ @. @. \\ X \otimes A \\ @V{f}VV \\ Y \\ @. @. \\ Y \\ @V{q}VV \\ Y' \ \end{CD}$

自然性は次の3つの等式で表現できます。

タイトニング

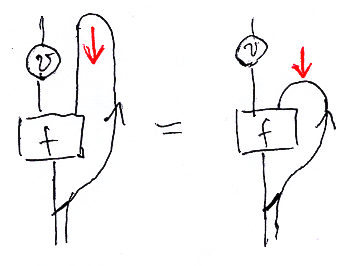
$\Lambda^{X',A}_Y( (v\otimes id_A);f) = v;\Lambda^{X,A}_Y(f)$

絵だと、曲がったワイヤーの部分（ベント）を短く締め込んでいるいるのでタイトニング〈tightening〉と呼びます。もともとは、タイトニング／スライディングはトレースの自然性を表す言葉です（「トレース付き対称モノイド圏とはこんなモノ」参照）。

簡略なラムダ式で表すなら：

λa.f(v(x'), a) = (λa.f(x, a))[v(x')/x]

ここで、[v(x')/x] は、変数xにv(x')を代入するオペレーターです。

カーブに沿ったスライディング

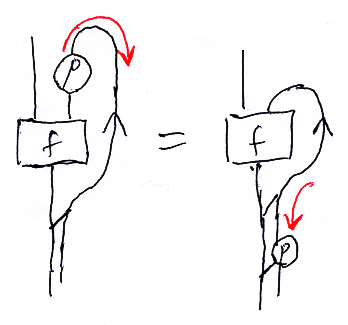
$\Lambda^{X,A'}_Y( (id_X\otimes p);f ) = \Lambda^{X,A}_Y(f);[p, Y]$

絵だと、ノードpを曲がったワイヤーに沿って滑らしているのでカーブに沿ったスライディング〈curved sliding〉と呼びます。移動後のpは指数の内部に入ります。

簡略なラムダ式で表すなら：

λa'.f(x, p(a')) = Y^p(w)[λa.f(x, a)/w]

ここで、Y^p は [p, Y] と同じで、指数関手〈内部ホム関手〉に p, id_Y を渡した結果です。

真っすぐなスライディング

$\Lambda^{X,A}_{Y'}( f;q ) = \Lambda^{X,A}_Y(f);[A, q ]$

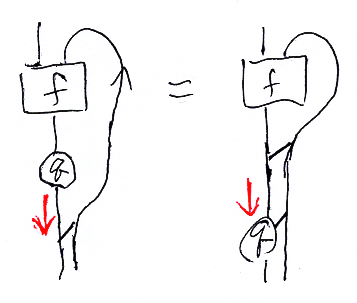
絵だと、ノードqを真っすぐに下に滑らしているので真っすぐなスライディング〈straight sliding〉と呼びます。移動後のqは指数の内部に入ります。

簡略なラムダ式で表すなら：

λa.q(f(x, a)) = q^A(w)[λa.f(x, a)/w]

自然性をまとめてみると

タイトニング、カーブに沿ったスライディング、真っすぐなスライディングの3つの操作をまとめると次のようになります。

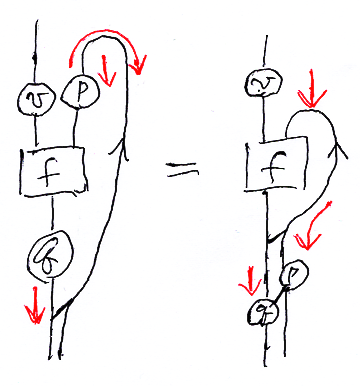
$\Lambda^{X',A'}_{Y'}( (v\otimes p);f;q ) = v;\Lambda^{X,A}_Y(f);[p, q]$

さらにまとまりを付けるために、Φ^v,p_q と Φ^v_{[p, q]} を次のように定義します。

$\Phi^{v,p}_{q}:{\mathcal C}(X \otimes A, Y) \to {\mathcal C}(X' \otimes A', Y') \\ \Phi^{v,p}_{q}(f) := (v \otimes p);f;q \\ \: \\ \Phi^{v}_{[p, q]}:{\mathcal C}(X, [A, Y]) \to {\mathcal C}(X', [A', Y']) \\ \Phi^{v}_{[p, q]}(g) := v;g;[p, q] \\$

これらを使うと、カリー化の自然性は次のように書けます。

$\Lambda^{X', A'}_{Y'}(\Psi^{v,p}_{q}(f)) = \Psi^{v}_{[p, q]}(\Lambda^{A,X}_{Y}(f))$

可換図式ならば：

$\begin{CD} {\mathcal C}(X'\otimes A', Y') @>{\Lambda^{X', A'}_{Y'}}>> {\mathcal C}(X', [A', Y']) \\ @A{\Psi^{v,p}_{q}}AA @AA{\Psi^{v}_{[p, q]}}A \\ {\mathcal C}(X\otimes A, Y) @>{\Lambda^{A,X}_{Y}}>> {\mathcal C}(X, [A, Y]) \\ \end{CD}$

*1:左指数と右指数を区別して扱えばスッキリするのですが、対称モノイド圏では、左右を区別なしでやることが多いです。左右を区別しないほうが簡便ですが、代わりに多少の曖昧さと混乱が生じます。

*2:随伴系の一般論では、カリー化／反カリー化を転置／反転置とも呼びます。「圏論の随伴をちゃんと抑えよう // 転置と反転置」参照。