左随伴関係は関数

「左随伴関手は左カン拡張を保存する」で、左随伴関手が左カン拡張とうまく協調することを述べました。一般に、左随伴関手や右随伴関手は良い性質を持ちます。

この記事では、お馴染みで簡単な2-圏である関係の2-圏 $`{\bf Rel}`$ において左随伴関手相当の1-射が何であるかを調べてみます。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\msc}[1]{ \mathscr{#1} }
\newcommand{\dimU}[2]{{#1}\!\updownarrow^{#2}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\cat}[1]{\mathcal{#1}}`$

内容：

2-圏の概念と記法
随伴系
随伴系の横結合
ホム圏ごとにとてもやせている2-圏
関係の2-圏
単葉関係、全域関係、関数
単葉関係と全域関係の特徴付け
左随伴関係は関数

2-圏の概念と記法

2-圏は、対象〈0-射〉と射〈1-射〉以外に2-射を持つ構造です。ここでの2-圏は、厳密性を仮定していません。つまり、双圏を2-圏と呼んでいます。典型的な2-圏は小さい圏達を対象とする2-圏 $`{\bf Cat}`$ （これは厳密2-圏）です。$`{\bf Cat}`$ の2-圏構造は次のようになります。すぐ下の図は、対象〈0-射〉と射〈1-射〉だけ示しています。

対象〈0-射〉：小さい圏 $`\cat{C} \in |{\bf Cat}|`$
射〈1-射〉：関手 $`F:\cat{C} \to \cat{D} \In {\bf Cat}`$
恒等射〈恒等1-射〉：恒等関手 $`\mrm{Id}_\cat{C}:\cat{C}\to \cat{C} \In {\bf Cat}`$
2-射：自然変換 $`\alpha :: F \twoto F' : \cat{C} \to \cat{D} \In {\bf Cat}`$
恒等2-射：恒等自然変換 $`\mrm{ID}_F :: F \twoto F : \cat{C} \to \cat{D} \In {\bf Cat}`$
射〈1-射〉の横結合：関手の結合 $`F*G : \cat{C} \to \cat{E} \In {\bf Cat}`$
2-射の横結合：自然変換の横結合 $`\alpha *\beta:: F*G \twoto F'*G' : \cat{C} \to \cat{E} \In {\bf Cat}`$
2-射の縦結合：自然変換の縦結合 $`\alpha ; \alpha' :: F \twoto F'' : \cat{C} \to \cat{D}\In {\bf Cat}`$

$`\quad \xymatrix@C+2pc{
\cat{C} \ar@/^1.5pc/[r]^{F} \ar[r]|{F'} \ar@/_1.5pc/[r]_{F''}
& \cat{D} \ar@/^1.5pc/[r]^{G} \ar[r]|{G'}
& \cat{E}
}`$

モノイド圏 $`M`$ は、対象を唯一つだけ持つ2-圏とみなせます。

対象〈0-射〉：唯一つの対象 $`\star`$
射〈1-射〉：モノイド圏の対象 $`A \in |\cat{M}|`$
恒等射〈恒等1-射〉：モノイド圏の単位対象 $`\mrm{I}\in |\cat{M}|`$
2-射：モノイド圏の射 $`f: A \to A' \In \cat{M}`$
恒等2-射：モノイド圏の恒等射 $`\mrm{id}_A : A \to A \In \cat{C}`$
射〈1-射〉の横結合：対象のモノイド積 $`A\otimes B \in |\cat{M}|`$
2-射の横結合：射のモノイド積 $`f\otimes g : A\otimes B \to A'\otimes B' \In \cat{M}`$
2-射の縦結合：射の結合 $`f; f' : A \to A'' \In \cat{M}`$

$`\quad \xymatrix@C+2pc{
\star \ar@/^1.5pc/[r]^{A} \ar[r]|{A'} \ar@/_1.5pc/[r]_{A''}
& \star \ar@/^1.5pc/[r]^{B} \ar[r]|{B'}
& \star
}`$

2-圏〈双圏〉の定義については、「この2つのミニマムな解説はほんとに便利だ」で紹介したレンスター〈Tom Leinster〉の "Basic Bicategories" などを参照してください。

一般的2-圏（双圏） $`\cat{K}`$ に対して、次の記法を採用します。

対象〈0-射〉： $`A \in |\cat{K}|`$
射〈1-射〉： $`f:A \to B \In \cat{K}`$
恒等射〈恒等1-射〉： $`\mrm{id}_A : A \to A \In \cat{K}`$
2-射： $`\alpha :: f \twoto f' : A\to B \In \cat{K}`$
恒等2-射： $`\mrm{Id}_f :: f \twoto f : A\to B \In \cat{K}`$
射〈1-射〉の横結合： $`f * g : A \to C \In \cat{K}`$
2-射の横結合： $`\alpha * \beta :: f*g \twoto f'*g' : A \to C \In \cat{K}`$
2-射の縦結合： $`\alpha ; \alpha' :: f \twoto f'' : A \to B \In \cat{K}`$

$`\quad \xymatrix@C+2pc{
A \ar@/^1.5pc/[r]^{f} \ar[r]|{f'} \ar@/_1.5pc/[r]_{f''}
& B \ar@/^1.5pc/[r]^{g} \ar[r]|{g'}
& C
}`$

行きがかり上、恒等射の書き方がバラバラで重複（名前のコンフリクト）もあります。

	圏の2-圏	モノイド圏	一般の2-圏
恒等1-射	$`\mrm{Id}`$	$`\mrm{I}`$	$`\mrm{id}`$
恒等2-射	$`\mrm{ID}`$	$`\mrm{id}`$	$`\mrm{Id}`$

随伴系

2-圏 $`\cat{K}`$ のなかで随伴系〈adjunction | adjoint system〉を考えます。$`f`$ を左1-射、$`g`$ を右1-射とする随伴系を次のように書きます。

$`\quad (f:A \to B) \dashv (g : B \to A) \text{ by }\eta, \varepsilon \In \cat{K}`$

この随伴系を $`\msc{A}`$ と置くと、各構成素は次のように呼びます。

$`f`$ は、随伴系 $`\msc{A}`$ の左1-射
$`g`$ は、随伴系 $`\msc{A}`$ の右1-射
$`\eta`$ は、随伴系 $`\msc{A}`$ の単位2-射
$`\varepsilon`$ は、随伴系 $`\msc{A}`$ の余単位2-射

単位と余単位のプロファイルは次のようになります。

$`\quad \eta :: \mrm{id}_A \twoto f*g : A \to A \In \cat{K}\\
\quad \varepsilon :: g*f \twoto \mrm{id}_B : B \to B \In \cat{K}
`$

名前を節約するために、随伴系の構成素である左右の1-射を次のように書くことがあります。

$`\quad f^* \dashv f_*`$

あるいは、片方にだけ星印を付けて：

$`\quad f^* \dashv f`$
$`\quad f \dashv f_*`$

「左随伴」「右随伴」は、もともと随伴系における構成素の役割名ですが、2-圏 $`\cat{K}`$ の1-射 $`h`$ に対して「$`h`$ は左随伴／右随伴である」という使い方もします。これは次の意味です。

$`h`$ が左随伴〈left adjoint〉であるとは、$`h`$ を左1-射として含む随伴系が存在すること。
$`h`$ が右随伴〈rightt adjoint〉であるとは、$`h`$ を右1-射として含む随伴系が存在すること。

この記事では、構成素の役割名には「左1-射／右1-射」を使い、2-圏の1-射に対する形容詞として使うときは「左随伴／右随伴」を使います。

随伴系の横結合

$`\cat{K}`$ を2-圏として、$`\msc{A}`$ と $`\msc{A'}`$ を2つの随伴系とします。

$`\quad \msc{A} = \big(\, (f:A \to A') \dashv (f_* : A' \to A) \text{ by }\eta, \varepsilon \,\big)
\quad \msc{A'} = \big(\, (f':A' \to A'') \dashv ({f'}_* : A'' \to A') \text{ by }\eta', \varepsilon' \,\big)
`$

$`\msc{A}`$ と $`\msc{A'}`$ の（図式順の）横結合は次のように定義できます。

$`\quad \msc{A}*\msc{A'} :=
\big(\,
(f*f':A \to A'') \dashv (f'_* * f_* : A'' \to A) \text{ by }\eta;\eta', \varepsilon';\varepsilon
\,\big)
`$

$`\eta;\eta'`$ だけ絵（ストリング図）に描くと次のようです。

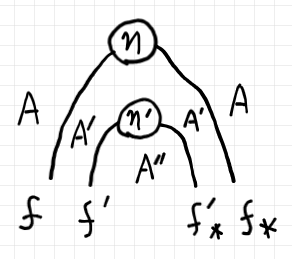
$`\msc{A}*\msc{A'}`$ が、随伴系の等式的法則〈公理〉であるニョロニョロ法則〈snake {law | relation | equation | identity}〉を満たすことも簡単に示せます。さらに、随伴系達は横結合で圏になります。恒等は次の自明な随伴系です。

$`\quad \msc{I}_A := \big(\, (\mrm{id}_A:A \to A) \dashv (\mrm{id}_A : A \to A) \text{ by }\mrm{Id}_{\mrm{id}_A}, \mrm{Id}_{\mrm{id}_A} \,\big)`$

2-圏 $`\cat{K}`$ 内の随伴系達が作る圏は、過去記事の記号に合わせると $`{_1\mrm{Adj}_L}(\cat{K})`$ と書けます。下付きで $`1, L`$ が付いているのは、1-圏であって、随伴系の向きを左1-射の向きに取るという意味です。

随伴系達は、1-圏だけでなくてより複雑な構造にもなり得ます。それについては以下の過去記事を参照してください。

$`\cat{K}`$ の随伴系達が、上に定義した横結合で圏となることから、$`\cat{K}`$ の左随伴1-射（随伴系の左1-射である1-射）達は圏を形成します。右随伴1-射達も圏を形成します。次の記法を使います。

2-圏 $`\cat{K}`$ の対象を対象として、左随伴1-射を射とする圏を $`\mrm{LAdj}(\cat{K})`$ と書く。
2-圏 $`\cat{K}`$ の対象を対象として、右随伴1-射を射とする圏を $`\mrm{RAdj}(\cat{K})`$ と書く。

随伴系から左1-射を取り出す関手を $`{L}`$ 、右1-射を取り出す関手を $`{R}`$ とすると、次のようになります。

$`\quad L :\, {_1 \mrm{Adj}_L}(\cat{K}) \to \mrm{LAdj}(\cat{K}) \subseteq \dimU{\cat{K}}{1} \In {\bf CAT}\\
\quad R :\, {_1 \mrm{Adj}_R}(\cat{K}) \to \mrm{RAdj}(\cat{K}) \subseteq \dimU{\cat{K}}{1} \In {\bf CAT}
`$

ここで、$`\dimU{\cat{K}}{1}`$ は、2-圏 $`\cat{K}`$ の2-射を捨てた1-圏です。$`\dimU{\text{－}}{1}`$ については「圏の次元調整」を参照してください。

ホム圏ごとにとてもやせている2-圏

圏 $`\cat{C}`$ がやせている〈thin〉とは、任意のホムセット $`\cat{C}(A, B)`$ が空集合か単元集合であることです。圏 $`\cat{C}`$ が骨格的〈skeletal〉とは、対象 $`A, B`$ が同型なら $`A = B`$ であることです。やせていて骨格的な圏はとてもやせている〈very thin〉といいます。やせた圏 $`\cat{C}`$ は、$`|\cat{C}|`$ を台集合とするプレ順序集合〈preordered set〉になります。とてもやせていれば順序集合になります。

$`\cat{K}`$ を2-圏として、任意のホム圏 $`\cat{K}(A, B)`$ がやせているならホム圏ごとにやせている〈hom-wise thin〉と呼ぶことにします。任意のホム圏 $`\cat{K}(A, B)`$ がとてもやせているならホム圏ごとにとてもやせている〈hom-wise very thin〉2-圏です。ホム圏ごとにとてもやせている2-圏は、順序集合で豊穣化された圏〈$`{\bf Ord}`$-enriched category〉ですが、ここでは、2-圏の特別なものとして扱います。

ここから先、$`\cat{K}`$ はホム圏ごとにとてもやせた2-圏とします。2-射 $`\alpha :: f \twoto f'`$ は存在するとしても唯一つです。2つの1-射が2-圏内で同値 $`f \simeq f'`$ （ホム圏内で同型）ならば $`f = f'`$ です。

ホム圏ごとにとてもやせた2-圏 $`\cat{K}`$ 内に、次のような2-射 $`\alpha, \beta`$ があるとします。

$`\quad \alpha :: \mrm{Id}_A \twoto f*g : A \to A \In \cat{K}\\
\quad \beta :: g*f \twoto \mrm{Id}_B : B \to B \In \cat{K}
`$

このとき、$`\alpha,\beta`$ は自動的にニョロニョロ法則を満たし、$`f, g, \alpha,\beta`$ は随伴系を構成します。それは、ホム圏ごとにやせていることだけから出ます。以下に示します。

次のような2-射は定義できます。

$`\quad \varphi := (\alpha * \mrm{Id}_f); (\mrm{Id}_f * \beta) :: f \twoto f : A \to B \In \cat{K}\\
\quad \psi := (\mrm{Id}_g * \alpha ); (\beta * \mrm{Id}_g ) :: g \twoto g : B \to A \In \cat{K}
`$

ホム圏で見ると：

$`\quad \varphi : f \to f \In \cat{K}( A, B)\\
\quad \psi : g \to g \In : \cat{K}(B, A)
`$

ホム圏はやせているので、$`\varphi = \mrm{Id}_f`$ 、 $`\psi = \mrm{Id}_g`$ となりますが、これは随伴系のニョロニョロ法則に他なりません。（ストリング図を描いてみればほぼ自明な話。）

$`\cat{K}`$ の1-射 $`f:A \to B`$ が左随伴だとします。これは、$`f`$ を左1-射、$`g:B \to A`$ を右1-射とする随伴系 $`\msc{A}`$ が存在することです。一般には、随伴系 $`\msc{A}`$ が存在しても一意性は言えません。しかし、$`\cat{K}`$ がホム圏ごとにとてもやせている場合は、$`\msc{A}`$ の、したがって $`g`$ の一意性が言えます。それを示しましょう。

$`f`$ を左1-射として含む2つの随伴系 $`\msc{A}, \msc{A'}`$ があったとします。

$`\quad \msc{A} = \big(\, (f:A\to B) \dashv (g:B \to A)\text{ by }\eta, \varepsilon \,\big)\\
\quad \msc{A'} = \big(\, (f:A\to B) \dashv (g':B \to A)\text{ by }\eta', \varepsilon' \,\big)
`$

次のような2-射は定義できます。

$`\quad \sigma := (\eta' *\mrm{Id}_g) ; (\mrm{Id}_{g'} * \varepsilon) :: g \twoto g' : B \to A \In \cat{K}\\
\quad \tau := (\mrm{Id}_g * \eta ) ; (\varepsilon' * \mrm{Id}_{g}) :: g' \twoto g' : B \to A \In \cat{K}
`$

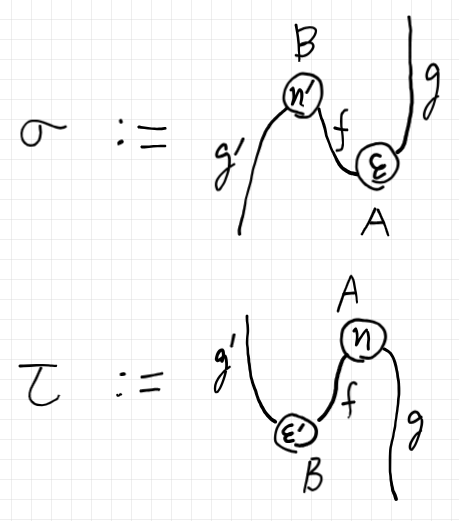
ホム圏で見ると：

$`\quad \sigma : g \to g' \In \cat{K}(B, A)\\
\quad \tau : g' \to g \In \cat{K}(B, A)
`$

やせている圏のなかで、双方向に射があれば、それらの対象は同型です。

$`\quad g \cong g' \In \cat{K}(B, A)`$

ホム圏はとてもやせていたので、骨格的であり、同型な対象は同一です。

$`\quad g = g' \In \cat{K}(B, A)`$

これで、左随伴な1-射 $`f`$ のパートナーとなる右1-射が一意的であることが分かりました。

$`\cat{K}`$ がホム圏ごとにとてもやせている場合の特殊事情をまとめると：

随伴系の素材さえ揃えば、ニョロニョロ法則を示す必要はない。自動的に満たされる。
左随伴1-射に対して、パートナー右1-射は一意的に決まる。

関係の2-圏

タイトルにある「左随伴関係は関数」は、2-圏とみなした関係圏の1-射が左随伴なら、それは関数であるということです。これを示すには、まず関係の2-圏を定義する必要があります。関係の2-圏も、関係の1-圏と同じ名前 $`{\bf Rel}`$ をオーバーロードして使います。

$`{\bf Rel}`$ の対象は、集合 $`A, B`$ など。
$`{\bf Rel}`$ の射〈1-射〉は、関係 $`R\subseteq A\times B`$ など。
$`{\bf Rel}`$ の2-射は、関係のあいだの包含関係 $`R \subseteq S`$ 。

2-圏のフレームワークに合わせるために、次の記法を使います。

対象〈0-射〉： $`A \in |{\bf Rel}|`$ 、$`A`$ は集合。
射〈1-射〉： $`R:A \to B \In {\bf Rel}`$ 、これは $`R\subseteq A\times B`$ のこと。
恒等射〈恒等1-射〉： $`\mrm{Id}_A : A \to A \In {\bf Rel}`$ 、$`\mrm{Id}_A \subseteq A\times A`$ は対角集合。
2-射： $`\alpha :: R \twoto R' : A\to B \In {\bf Rel}`$ 、これは $`R\subseteq R'`$ のこと。
恒等2-射： $`\mrm{ID}_R :: R \twoto R : A\to B \In {\bf Rel}`$ 、これは $`R \subseteq R`$ のこと。
射〈1-射〉の横結合： $`R * S : A \to C \In {\bf Rel}`$ 、関係の結合（図式順）
2-射の横結合： $`\alpha * \beta :: R*S \twoto R'*S' : A \to C \In {\bf Rel}`$ 、関係のあいだの包含関係が結合で保存されること。
2-射の縦結合： $`\alpha ; \alpha' :: R \twoto R'' : A \to B \In {\bf Rel}`$ 、包含関係の推移律。

$`{\bf Rel}(A, B)`$ は、集合としてはベキ集合 $`\mrm{Pow}(A\times B)`$ と同じものです。ベキ集合 $`\mrm{Pow}(A\times B)`$ には、部分集合の包含順序で順序構造が入ります。順序関係を射とみてとてもやせた圏になります。つまり、$`{\bf Rel}`$ のすべてのホム圏はとてもやせた圏です。

2-圏 $`{\bf Rel}`$ に対しては、ホム圏ごとにとてもやせた2-圏の議論が通用します。

単葉関係、全域関係、関数

関係 $`R:A \to B \In {\bf Rel}`$ が単葉〈univalent〉とは次のことです。

$`\quad \forall a\in A.\forall b, b'\in B.(\, (a, b)\in R \land (a, b')\in R \, \Imp b = b' \,)`$

自然言語文で表現すれば：

　　集合 $`A`$ の任意の要素 $`a`$ に対して、
　　　　集合 $`B`$ の任意の2つの要素 $`b, b'`$ （異なる要素とは言ってない）に対して、
　　　　$`(a, b)\in R`$ と $`(a, b')\in R`$ がともに成立するならば、$`b`$ と $`b'`$ は同一である。

注意すべきは、「$`(a, b)\in R \land (a, b')\in R `$ となる $`a, b, b'`$ が存在する」とは言ってないことです。もし前件 $`(a, b)\in R \land (a, b')\in R`$ が成立するならば、$`b = b'`$ となる、と言っているだけです。

関係から誘導される非決定性写像で考えたほうが分かりやすいかも知れません。関係 $`R \subseteq A\times B`$ があると、$`A \to \mrm{Pow}(B)`$ という写像（値が部分集合である写像）が決まります。これを $`A`$ から $`B`$ への非決定性写像と呼びます。非決定性写像（値が部分集合である写像）の値を（通常の記法で） $`R(a)`$ と書くことにすると：

$`\quad R(a) := \{y\in B\mid (a, y) \in R \}\; \in \mrm{Pow}(B)`$

$`R(a)`$ を使って $`R`$ が単葉であることを書くと：

$`\quad \forall a\in A.(\, R(a) = \emptyset \lor R(a) \cong {\bf 1} \,)`$

自然言語文で表現すれば：

　　集合 $`A`$ の任意の要素 $`a`$ に対して、
　　　　（$`B`$ の部分集合である）$`R(a)`$ は、
　　　　空集合であるか、または単元集合（特定された単元集合 $`{\bf 1}`$ と同型）である。

$`R`$ が単葉のとき、$`R(a)`$ は空集合か単元集合なので、次のようにして $`A`$ 上の部分関数とみなせます。

$`R(a)`$ が空集合のとき、部分関数の値は未定義とする。
$`R(a)`$ が単元集合のとき、部分関数の値は単元集合の唯一の要素とする。

さて次に、関係 $`R:A \to B \In {\bf Rel}`$ が全域〈total〉であることを定義します。全域であるとは次のことです。

$`\quad \forall a\in A.\exists b \in B.(\, (a, b)\in R \,)`$

自然言語文で表現すれば：

　　集合 $`A`$ の任意の要素 $`a`$ に対して、
　　　　$`(a, b)\in R`$ となる集合 $`B`$ の要素 $`b`$ が存在する。

こっちは分かりやすいでしょう。$`R(a)`$ を使って書けば：

$`\quad \forall a\in A.(\, R(a) \ne \emptyset \,)`$

関係 $`R:A \to B\In {\bf Rel}`$ が単葉なら部分関数を定義します。さらに $`R`$ が全域であれば、関数を定義します。単元集合 $`R(a)`$ から要素を取り出す操作は必要ですが、キャッチフレーズとしては次のように言っていいでしょう。

単葉全域な関係は関数である。

単葉関係と全域関係の特徴付け

関係 $`R:A\to B\In {\bf Rel}`$ に対して、その転置〈transpose〉 $`R^t`$ は次のように定義します。

$`\quad R^t := \{(b, a) \in B\times A\mid (a, b)\in R\}\; : B\to A \In {\bf Rel}`$

関係 $`R`$ が単葉であることは、転置と恒等関係 $`\mrm{Id}_B`$ を使って次のように書けます。

$`\quad R^t * R \subseteq \mrm{Id}_B`$

これをブレークダウンしましょう。集合としての $`R^t * R`$ は次のように書けます。

$`\quad R^t * R = \{(b, b')\in B\times B\mid \exists a\in A.\, (b, a)\in R^t \land (a, b') \in R\}`$

よって、上記の包含関係は次のとおりです。

$`\quad\{(b, b')\in B\times B\mid \exists a\in A.\, (b, a)\in R^t \land (a, b') \in R \}\\
\qquad \subseteq \{(b, b') \in B\times B\mid b = b'\}
`$

同じことを論理式だけで書き下すと：

$`\quad \forall (b, b') \in B\times B.(\,
(\exists a\in A.\, (b, a)\in R^t \land (a, b') \in R) \Imp b = b' \,)
`$

$`(b, a) \in R^t`$ を $`(a, b)\in R`$ に書き換えておきます。

$`\quad \forall (b, b') \in B\times B.(\,
(\exists a\in A.\, (a, b)\in R \land (a, b') \in R) \Imp b = b' \,)
`$

これがほんとに $`R`$ の単葉性を定義しているのでしょうか？「ならば（記号は '$`\Imp`$'）」に対する誤解などから、この論理式を直感的に理解するのはけっこう難しいかも知れません。以下に直感的説明をします。

「存在するならば云々」という形の論理式は、存在を主張していません。「もし存在するならば」と言っているだけです。古典論理では、「存在するならば云々」は「存在しないかまたは云々」なので、存在しないときは「云々」がなんであっても問答無用に真です。上記の論理式を2つのケースに分けて解釈しましょう。

$`(a, b)\in R\land (a, b') \in R`$ である $`a`$ が存在しないとき：論理式は真だから、それ以上考える必要はない。
$`(a, b)\in R\land (a, b') \in R`$ である $`a`$ が存在するとき： $`b = b'`$ かどうかを考える必要がある。

2番目のケースを直感的な絵に描くと次のようになります。

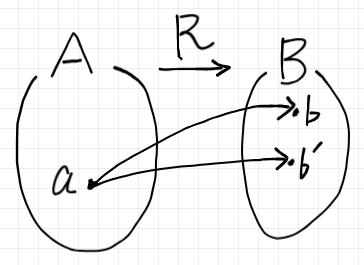
この状況で「$`b = b'`$」を要求すると、$`R(a)`$ が単元集合であるべきと言っています。つまり、当該の条件の内容は次のとおり。

$`R(a)`$ が空集合であってもかまわない。
$`R(a)`$ が空集合でないなら、単元集合でなくてはならない。

これは単葉性の条件です。

同様な議論により、関係 $`R`$ が全域であることは、次のようにも書けます。

$`\quad \mrm{Id}_A \subseteq R * R^t`$

関係 $`R:A \to B\In {\bf Rel}`$ が関数である（関数とみなせる）ことは、単葉かつ全域なので、次の包含関係が2つとも成立することです。

$`\quad R^t * R \subseteq \mrm{Id}_B\\
\quad \mrm{Id}_A \subseteq R * R^t
`$

上記2つの包含関係は、$`R`$ が関数であることを完全に特徴付けています。それは次の意味です。

上記2つの包含関係を満たす関係は、関数である（関数とみなせる）。
関数である関係は、上記2つの包含関係を満たす。

$`R:A\to B`$ は、ホム圏ごとにとてもやせた2-圏 $`{\bf Rel}`$ の1-射とします。$`R`$ は左随伴1-射だとします。つまり、随伴系 $`\msc{A}`$ とその右1-射 $`S:B\to A`$ が存在します。随伴系 $`\msc{A}`$ の単位と余単位は次のようです。

$`\quad \eta:: \mrm{Id}_A \twoto R * S : A \to A \In {\bf Rel}\\
\quad \varepsilon :: S * R \twoto \mrm{Id}_B : B \to B \In {\bf Rel}
`$

これらは、次の包含関係です。

$`\quad \mrm{Id}_A \subseteq R * S \In \mrm{Pow}(A \times A)\\
\quad S * R \subseteq \mrm{Id}_B \In \mrm{Pow}(B \times B)
`$

ホム圏ごとにとてもやせた2-圏の性質から、この連立包含関係は随伴系と同じことだし、$`S`$ は一意的に存在します。

前節の結果から、一意的に決まる $`S`$ は $`R^t`$ のことであり、$`R`$ が右随伴1-射〈右随伴関係〉であることは、実は、$`R`$ が関数であることだと分かります。