整数の加減乗除のなかにもひそんでいるヤン・バクスター方程式

ウガーッ、割り算はむずかしいなぁーー。

ウチの長男も割り算は苦手のようだが、僕もダメだ。アタマこんがらかって計算できないよー。挫折した。

正整数の加減乗除だけに関わる等式変形、うまくいかーん。余りが出る割り算をちゃんと知っていて、几帳面で、根気があれば普通に出来るハズのもの；僕は、余りが出る割り算をちゃんと知ってなくて、几帳面じゃないし、根気がないので出来ませんでした。誰かやってみない？（背景は後で少し説明します）

内容：

記法の準備
関数族c, s, t, u と略記法
等式群
とにかく実例を試してみる
これらの等式はいったい何なの？

●記法の準備

I, K, Lは正整数とします。「なんで、I, J, K じゃないの？」 -- それはですね、手書き計算で I, J, K を使っていたら、IとJ（あるいはiとj）をしょっちゅう見間違うんですよ。それで、Jはやめた。

「+, *, /, %」はそれぞれ「足し算、掛け算、整数の範囲内での割り算（整除）、割り算の余り」です。I*K は単に IK のように書き、掛け算が一番優先度が高いとします。ですから、x/IK は x/(I*K) ってことですね。i, x, z はそれぞれ次の範囲を走る整数変数だとします。

0 ≦ i < I
0 ≦ x < IK
0 ≦ z < IKL

今から、c_I(i), s_I,K(x), t_I,K,L(z), u_I,K,L(z) という関数を定義します。これらは、下付きで添えられた正整数をパラメータとする関数族になります。

●関数族c, s, t, u と略記法

c_I(i) = i
s_I,K(x) = (x%K)I + x/K
t_I,K,L(z) = s_{I, K}(z/L)*L + z%L
u_I,K,L(z) = (z/KL)*LK + s_{K, L}(z%KL)

さらに、表記を簡単にするために、次の略記を使います。

[I](i) = c_I(i)
[I, K](x) = s_I,K(x)
[I, K; L](z) = t_I,K,L(z)
[I; K, L](z) = u_I,K,L(z)

●等式群

関数の反図式順（右から左への）結合（合成）を「・」で示します。つまり、(f・g)(x) = f(g(x)) 。さて、以下の等式が成り立つハズです。

[K, I]・[I, K] = [IK]
[K, L; I]・[K; I, L]・[I, K; L] = [L; I, K]・[I, L; K]・[I; K, L]

これらの等式は、以下の図に対応します（後で少し説明します）。

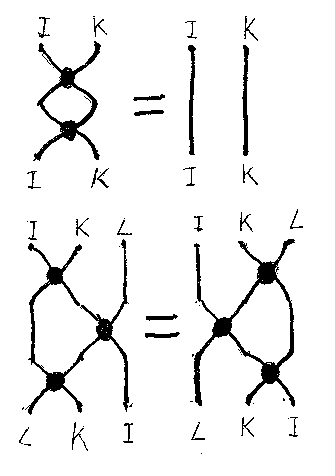
●とにかく実例を試してみる

後で述べる理由から、一番目の等式（恒等式、関係式）を対称方程式（Symmetry Equation）、二番目の等式をヤン・バクスター（Yang-Baxter）方程式と呼びます。これらは、整数の加減乗除しか使ってないので、実例を確認するプログラムは簡単に作れます。JavaScript（処理系はRhino）で書いてみました（JSLintを通してますよ :-) ）。



function div(n, k) {

  return Math.floor(n/k);

}
function c(I) {

  return function(i) {return i;};

}
function s(I, K) {

  return function(x) {

    return (x%K)*I + div(x, K);

  };

}
/* Symmetry Equation:

 * y = s(K, I)(s(I, K)(x))

 * ----------------------

 * y == x 

 */

function verifySEq(I, K) {

  var x, y;

  for (x = 0; x < I*K; x++) {

    y = s(K, I)(s(I, K)(x));

    if (y != x) {

      return "NG";

    }

  }

  return "OK";

}
function t(I, K, L) {

  return function(z) {

    return s(I, K)(div(z, L))*L + z%L;

  };

}
function u(I, K, L) {

  return function(z) {

    return div(z, K*L)*(L*K) + s(K, L)(z%(K*L));

  };

}
/* Yang-Baxter Equation:

 * w1 = t(K, L, I)(u(K, I, L)(t(I, K, L)(z)))

 * w2 = u(L, I, K)(t(I, L, K)(u(I, K, L)(z)))

 * ------------------------------------------

 * w1 == w2

 */

function verifyYBEq(I, K, L) {

  var z, w1, w2;

  for (z = 0; z < I*K*L; z++) {

    w1 = t(K, L, I)(u(K, I, L)(t(I, K, L)(z)));

    w2 = u(L, I, K)(t(I, L, K)(u(I, K, L)(z)));

    if (w1 != w2) {

      return "NG";

    }

  }

  return "OK";

}

関数verifySEqとverifyYBEqが、それぞれ対称方程式とヤン・バクスター方程式の事例を確認します。



js> verifySEq(2, 3)

OK

js> verifySEq(3, 5)

OK

js> verifySEq(1, 4)

OK

js> verifyYBEq(2, 3, 4)

OK

js> verifyYBEq(4, 2, 5)

OK

js> verifyYBEq(1, 3, 7)

OK

js>

個別事例をいくら確認しても一般的な証明にはなりませんが、まー、状況証拠にはなります。

●これらの等式はいったい何なの？

「アミダのクイズをErlangで解いてみるよ」の「アルゴリズムの背景：アルチン変形」のところで出した絵を再掲します。

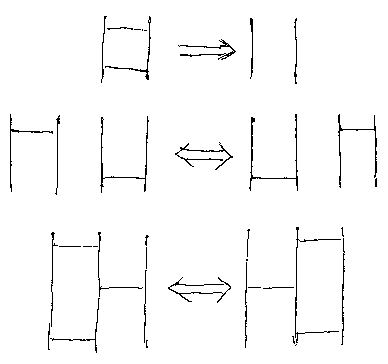
このアミダの横棒を交差する線にする（下の図）と、このエントリーの上のほうにある絵と同じようになるでしょ、上の図はオダンゴで交点を強調しているけど。（詳しくは「はじめての圏論中間付録B：アミダとブレイド」参照）

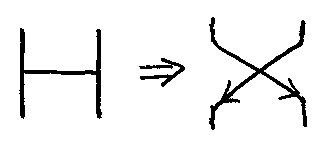
要するに僕はアミダの話をしていたのでした。アミダの交差（横棒）に関する基本的な法則は、アルチン（Artin）の関係式とかヤン・バクスター方程式と呼ばれています。これらは、本来はブレイドに関する等式ですが、簡略化するとそのままアミダでも成立してます。

アミダ図は、縦につなぐ操作（結合）と横に並べる操作（積）でモノイド圏になります。アミダ図をブレイド風に描いて、紐に正整数を割り振った図を考えます。紐に付いた正整数を仮に紐の厚みとでも呼んでおきましょう。雰囲気としては、紐をリボンケーブルと考え、ケーブルの厚みは線の本数だと考えます。最初に出した図は、厚み付き紐（リボンケーブル）のアミダ図で、I, K, Lなどが紐の厚みを示しています。

実は、厚み付き紐からできたアミダ図のモノイド圏は、整数の加減乗除の世界で表現できます。普通は、モノイド積を整数の足し算に対応させますが、今回はモノイド積が整数の掛け算に対応するようにしました。

対称方程式やヤン・バクスター方程式（その他、いろいろな方程式）は、もとのモノイド圏では自明に成立しているので、整数の加減乗除の世界でも成立しているのは道理なんですが、加減乗除だけで示すのは面倒ですね（余りの出る割り算が苦手なんで）。