等式的推論と高次圏論 - 檜山正幸のキマイラ飼育記 (はてなBlog)

$\newcommand{\mrm}[1]{\mathrm{#1}} % 必要 \newcommand{\cat}[1]{\mathcal{#1}} \newcommand{\In}{\text{ in } } \newcommand{\id}{\mathrm{id} } \newcommand{\Imp}{\Rightarrow }$ 圏論内で使う等式的推論を、圏論のなかで定式化してみます。等式的推論は高次射になるので、少しだけ高次圏論を使います。

内容：

等式的推論
高次圏
高次圏における結合
結合の演算子記号
恒等射
2-圏の3-射、4-射
恒等射だけの圏
恒等射の計算と等式的推論
おわりに

関連する記事：

等式的推論

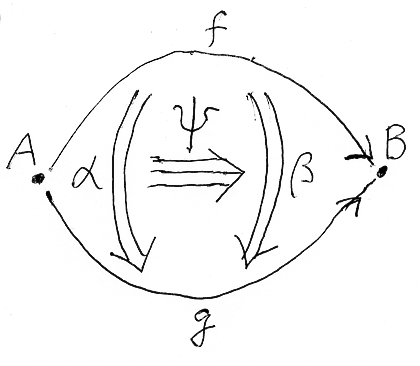
等式的推論〈equational reasoning〉は、幾つかの等式をもとに新しい等式を導き出す推論のことです。例えば次は、等式的推論における基本的な推論規則〈{inference | deduction} rule〉です。

$\quad \begin{array}{c c c} A = B & & B = C \\ \hline & A = C & \end{array}$

この推論規則の意味は、上段の2つの等式から下段の等式が導き出せる、ということです。等値関係〈equality〉の推移性〈transitivity〉がその根拠です。

等値関係の推移性： $A = B \land B = C \Imp A = C$

等式的推論は古典論理で統制されていて、ありとあらゆる分野で使われます。ただし、等号以外の関係記号／演算記号などの解釈は分野ごとに変わるでしょう。例えば、次の推論規則に出てくるセミコロンは“射の図式順結合記号”だとすれば、圏論における等式的推論になります。

$\quad \begin{array}{c c c} f = g & & h = k \\ \hline & f;h = g;k & \end{array}$

圏論における等式的推論も当然に古典論理の統制下にあります。古典論理の統制から逃れることは不可能です。が、しかし、圏論内で使われる等式的推論を、できる限り（古典論理ではなく）圏論内で定式化することには意味があります。自律的に自給自足しようという企てです。

基本的なアイディアは、等式を恒等射で置き換える、というものです。

高次圏

等式的推論を圏論内で定式化するには、通常の圏だけでなく高次圏〈higher category〉＝n-圏〈n-category〉の概念が必要です。とはいえ、厳密な定義や詳しい知識は不要で、次のことを認識していれば大丈夫です。

高次圏は、対象と射だけではなく、2次元の射、3次元の射、… など高次元の射を持つかも知れない。
対象は0次元の射、通常の射は1次元の射とみなす。
k次元の射も、域と余域を持ち、域・余域は(k - 1)次元の射である。ただし、0次元の射＝対象は例外で、域・余域を持たない。

k次元の射のことを短くk-射〈k-morphism〉と呼びます。0-射＝対象、1-射＝通常の射です。

各次元の射を表す文字を次のように約束します。

射の次元	文字種
0-射	ラテン大文字
1-射	ラテン小文字
2-射	ギリシャ小文字
3-射	ギリシャ大文字

例：

0-射： $A, B, C, D$
1-射： $f, g, h, k$
2-射： $\alpha, \beta, \phi, \psi$
3-射： $\Gamma, \Delta, \Phi, \Psi$

1-圏〈通常の圏〉 $\cat{C}$ の1-射〈通常の射〉 $f$ のプロファイル（域と余域の仕様）は次のように書きます。

$\quad f:A \to B \In \cat{C}$

同様に、高次射〈k-射〉のプロファイルは次のように書きます。3-圏 $\mathscr{X}$ 内の射だとします。下の図を参照してください。

$\quad f:A \to B \In \mathscr{X}\\ \quad g:A \to B \In \mathscr{X}\\ \quad \alpha:: f \Rightarrow g:A \to B \In \mathscr{X}\\ \quad \beta:: f \Rightarrow g:A \to B \In \mathscr{X}\\ \quad \Psi::: \alpha \equiv\!\gt \beta :: f \Rightarrow g : A \to B \In \mathscr{X}$

文字種の約束やプロファイルの書き方が広く合意されているわけではないので、他の約束・書き方があります。例えば、一番お馴染みの2-圏の例である“圏の圏” ${\bf Cat}$ では：

0-射〈対象〉はラテン大文字だが、カリグラフィー体 $\cat{C}, \cat{D}$ などで書く場合が多い。
1-射〈射〉はラテン大文字 $F, G$ などで書く場合が多い。

このような約束・書き方は、次元が上がれば破綻します。4-圏ではもうウマクないです。致し方ないので、4-射は次元を右肩に添えて示すことにします。

$\quad a^{(4)} :^4 \Psi \to^4 \Gamma ::: \alpha \equiv\!\gt \beta :: f \Rightarrow g : A \to B \In \mathscr{Y}$

ここで：

$a^{(4)}$ ： $a$ は4-射であることを示す。
$:^4$ ： $::::$ のこと。
$\to^4$ ：矢印の“太さ”が4本分であることを示す。

色々な約束・記号を使わずとも、右肩に添えた次元だけでも識別できますが、ちょっと味気なくなります。

$\quad a^{(4)} :^4 b^{(3)} \to^4 c^{(3)} :^3 d^{(2)} \to^3 e^{(2)} :^2 f^{(1)} \to^2 g^{(1)} : h^{(0)} \to i^{(0)} \In \mathscr{Y}$

高次圏における結合

1-圏〈通常の圏〉の1-射〈通常の射〉は結合〈compose〉できます。しかし、勝手な1-射を2つ持ってきても結合できるとは限りません。結合できるためには、2つの射が隣接している、あるいは境界を接している必要があります。 $f$ と $g$ が（この順で）隣接していることをハッキリと書くと：

$\quad \mrm{cod}(f) = \mrm{dom}(g)$

高次圏においても、隣接するk-射は結合できます。しかし、隣接の仕方が多様になります。次の図は、2つの2-射が隣接している様子を隣接境界部分を引き離して描いたものです。図の左側の場合は、1-射 $g$ を境界として隣接しています。図の右側の場合は、0-射 $B$ を境界として隣接しています。

プロファイルをハッキリと書くと：

$\quad \alpha::f \Rightarrow g :A \to B \In \cat{K}\\ \quad \beta ::g \Rightarrow h :A \to B \In \cat{K}\\ \quad \gamma ::v \Rightarrow w :B \to C \In \cat{K}$

図の左側では、 $\alpha$ と $\beta$ は1次元の境界 $g$ を介して（この順で）隣接しています。一方、図の右側では、 $\alpha$ と $\gamma$ は0次元の境界 $B$ を介して（この順で）隣接しています。隣接条件を明示的に書くなら：

$\quad \mrm{cod}(\alpha) = \mrm{dom}(\beta) = g\\ \:\\ \quad \mrm{cod}(\mrm{dom}(\alpha)) = \mrm{dom}(\mrm{dom}(\gamma) ) = B\\ \quad \mrm{cod}(\mrm{cod}(\alpha)) = \mrm{dom}(\mrm{cod}(\gamma) ) = B$

(k, j)-結合〈(k, j)-composition〉とは、j次元境界を介して隣接している2つのk-射に対して定義される結合です。今の例で言うなら：

2-射 $\alpha$ と2-射 $\beta$ は、1-射 $g$ を介して隣接しているので、(2, 1)-結合可能である。（図の左側）
2-射 $\alpha$ と2-射 $\gamma$ は、0-射 $B$ を介して隣接しているので、(2, 0)-結合可能である。（図の右側）

3次元の場合も見ておきましょう。

図の意味は次のようです。

左側は、2-射 $\beta$ を介して隣接している2つの3-射
真ん中は、1-射 $g$ を介して隣接している2つの3-射
右側は、0-射 $B$ を介して隣接している2つの3-射

3-射のプロファイルを書きましょう。

$\quad \Gamma ::: \alpha \equiv\!\gt \beta :: f \Rightarrow g : A \to B \In \mathscr{X}\\ \quad \Delta ::: \beta \equiv\!\gt \gamma :: f \Rightarrow g : A \to B \In \mathscr{X}\\ \quad \Phi ::: \phi \equiv\!\gt \psi :: g \Rightarrow h : A \to B \In \mathscr{X}\\ \quad \Psi ::: \sigma \equiv\!\gt \tau :: v \Rightarrow w : B \to C \In \mathscr{X}$

この状況で、3-射の結合可能性は次のようになります。

3-射 $\Gamma$ と3-射 $\Delta$ は、2-射 $\beta$ を介して隣接しているので、(3, 2)-結合可能である。（図の左側）
3-射 $\Gamma$ と3-射 $\Phi$ は、1-射 $g$ を介して隣接しているので、(3, 1)-結合可能である。（図の真ん中）
3-射 $\Gamma$ と3-射 $\Psi$ は、0-射 $B$ を介して隣接しているので、(3, 0)-結合可能である。（図の右側）

3-圏の場合は、(3, 2)-結合、(3, 1)-結合、(3, 0)-結合、(2, 1)-結合、(2, 0)-結合、(1, 0)-結合の6つの結合を備えています*4。一般に、n-圏には $\frac{n (n + 1)}{2}$ 個の結合があります。

結合の演算子記号

結合は二項演算なので、（二項中置の）演算子記号を使うのが普通です。2-圏の場合3つの結合演算がありますが、僕は次のような記号を使っています。詳しくは「関手と自然変換の計算に出てくる演算子記号とか // 今後使う予定の演算子記号」を参照してください。煩雑さを避けて、図式順演算子記号だけを載せます。

	2-射	1-射
1次元境界	$;$
0次元境界	$*$	$*$

新しい演算子記号 $*$ を下側（境界次元0）に挿入しているので、下側挿入方式と呼びましょう。これに対して、新しい演算子記号 $*$ を上側（境界次元1）に載せる方式を上側追加方式と呼びましょう。上側追加方式で演算子記号を決めると次のようになります。

	2-射	1-射
1次元境界	$*$
0次元境界	$;$	$;$

演算子記号の選択として、下側挿入方式も上側追加方式も両方使われていて一長一短があります。

ここでは、下側挿入方式で決めた2-圏の演算子記号に対して、上側追加方式により3-圏の演算子記号を決めます。次のようになります。

	3-射	2-射	1-射
2次元境界	$\&$
1次元境界	$;$	$;$
0次元境界	$*$	$*$	$*$

この決め方が、これから話す話題 -- つまり、2-圏における等式的推論の圏論的定式化には向いています。

さて、演算子記号の決め方はともかくとして、高次圏の結合はどのように定義され、どのような性質をもつのでしょうか？これに関する一般論は必要ないので省略します。結合律、単位律、交替律は成立します。法則は厳密に〈strictly〉成立するとは限らず、だいぶ込み入った関係になります。ややこしいのでこれ以上は触れません。

恒等射

1-圏〈通常の圏〉では、0-圏〈対象〉に対して恒等射がただひとつだけ決まります。n-圏でも同様です。

n-圏のk-射に対して、恒等(k + 1)-射がただひとつだけ決まる。

1-圏では、恒等射〈恒等1-射〉を $\id_A$ のように書きますが、ここでは下付き添字ではなく $\id(A)$ と書きます。そうしないと $\id_{\id_A}$ のように下付きが入れ子になり読みにくくなるからです。

恒等射の次元が分かりにくくなることがあるので、必要なら右肩に次元を添えます。

$\id^1(A)$ 0-射 $A$ の恒等1-射
$\id^2(f)$ 1-射 $f$ の恒等2-射
$\id^3(\alpha)$ 2-射 $\alpha$ の恒等3-射
$\id^4(\Gamma)$ 3-射 $\Gamma$ の恒等4-射

また、プロファイルの矢印に、その射が恒等射であるという情報を含めた次の書き方も使います。

$A \overset{\id}{\to} B$ 0-射 $A$ から $B$ への1-射があり、それは恒等1-射
$f \overset{\id}{\Rightarrow} g$ 1-射 $f$ から $g$ への2-射があり、それは恒等2-射
$\alpha \,\overset{\id}{\equiv\!\gt}\, \beta$ 2-射 $\alpha$ から $\beta$ への3-射があり、それは恒等3-射
$\Gamma \overset{\id}{\to^4} \Delta$ 3-射 $\Gamma$ から $\Delta$ への4-射があり、それは恒等4-射

$A \overset{\id}{\to} B$ は、 $A = B$ という等式命題と同じ意味です。その他の次元でも、恒等k-射は(k - 1)-射の等式命題と同じ意味です。これは、等式命題の代わりに恒等射を使ってもいいことを示します。そう、最初の節で述べたアイディア

等式を恒等射で置き換える

です。

2-圏の3-射、4-射

「n-圏には、次元がnより大きい射は存在しない」と考えるのが普通の態度ですが、どうもこれは不便なようです。どんなn-圏でも（空n-圏でない限り）、任意の次元の射が存在すると考えたほうが便利だと思います。例えば、2-圏には3-射も4-射も存在します。

では、2-圏の3-射／4-射とはどういうものでしょうか？それは恒等射です。2-圏 $\cat{K}$ の2-射 $\alpha, \beta$ があるとき、 $\alpha$ と $\beta$ のあいだの3-射とは次の恒等3-射だとします。

$\quad \alpha \,\overset{\id}{\equiv\!\gt}\, \beta \In \cat{K}$

別な言い方をすると、 $\alpha$ と $\beta$ のあいだの3-射とは $\alpha = \beta$ という等式です。恒等射〈等式〉にラベルを付けてもかまわないので、次のようにラベル付けします。
$\quad \Gamma ::: \alpha \,\overset{\id}{\equiv\!\gt}\, \beta \In \cat{K}\\ \quad \Delta ::: \alpha \,\overset{\id}{\equiv\!\gt}\, \beta \In \cat{K}$

この場合、3-射 $\Gamma$ と $\Delta$ は同じなので、次の4-射が存在します。

$\quad \Gamma \overset{\id}{\to^4} \Delta \In \cat{K}$

この4-射は、「2-射 $\alpha, \beta$ のあいだの等式のあいだの等式」と言えます。

このように考えれば、どんなn-圏でも、任意の次元の射が存在します。

恒等射だけの圏

n-圏 $\cat{K}$ のすべてのk-射からなる集合を $\mrm{Mor}^k(\cat{K})$ と書くことにします。特に：

$\mrm{Mor}^0(\cat{K}) = \mrm{Obj}(\cat{K}) = |\cat{K}|$
$\mrm{Mor}^1(\cat{K}) = \mrm{Mor}(\cat{K})$

$\cat{K}$ の恒等射だけからなる部分n-圏を $\mrm{Id}(\cat{K})$ とします。また、

$\quad \mrm{Id}^k(\cat{K}) := \mrm{Mor}^k(\mrm{Id}(\cat{K}))$

と約束します。次が成立します。

$\mrm{Id}^0(\cat{K}) = \mrm{Mor}^0(\cat{K})$
$\mrm{Id}^1(\cat{K}) \subseteq \mrm{Mor}^1(\cat{K})$
$\mrm{Id}^1(\cat{K}) \cong \mrm{Mor}^0(\cat{K})$

一般に：

$\mrm{Id}^k(\cat{K}) \subseteq \mrm{Mor}^k(\cat{K})$
$\mrm{Id}^k(\cat{K}) \cong \mrm{Mor}^{k - 1}(\cat{K})$

$n \lt l$ ならば：

$\mrm{Id}^l(\cat{K}) = \mrm{Mor}^l(\cat{K})$

つまり、十分高い次元では、 $\cat{K}$ と $\mrm{Id}(\cat{K})$ は区別がつきません。

恒等射だけからなるn-圏というと、非常につまらないn-圏のように思えますが、 $\mrm{Id}(\cat{K})$ には元のn-圏 $\cat{K}$ と同じだけの結合演算が備わっています。それらの結合演算や演算法則を考えれば、 $\mrm{Id}(\cat{K})$ はそれなりに面白い構造を持ちます。

恒等射の計算と等式的推論

$\cat{K}$ は2-圏だとして、 $\cat{K}$ の3-射まで考えます。3-射は2-射のあいだの恒等射（2-射の等式）です。この状況で、3-圏としての結合演算は6つあり、それらの演算記号は先の表（下に再掲）のように決めます。

	3-射	2-射	1-射
2次元境界	$\&$
1次元境界	$;$	$;$
0次元境界	$*$	$*$	$*$

この表のなかで、3-射（2-射の等式）に対する3つの演算 $\&, ;, *$ とは何でしょうか？結論を言ってしまうと、等式の推論規則です。以下に推論規則を列挙します。

2-射の等式の $\&$ -推論規則：

$\quad \begin{array}{c c c} \alpha = \beta & & \beta = \gamma \\ \hline & \alpha = \gamma & \end{array}$

2-射の等式の $;$ -推論規則：

$\quad \begin{array}{c c c} \alpha = \beta & & \phi = \psi \\ \hline & \alpha;\phi = \beta; \psi & \end{array}$

2-射の等式の $*$ -推論規則：

$\quad \begin{array}{c c c} \alpha = \beta & & \sigma = \tau \\ \hline & \alpha*\sigma = \beta * \tau & \end{array}$

これらの推論規則は分かりやすいと思いますが、射のプロファイル情報がハッキリしません。プロファイルを書き下します。

$\quad \alpha :: f \Rightarrow g: A \to B \In \cat{K}\\ \quad \beta :: f \Rightarrow g: A \to B \In \cat{K}\\ \quad \gamma :: f \Rightarrow g: A \to B \In \cat{K}\\ \quad \phi :: g \Rightarrow h: A \to B \In \cat{K}\\ \quad \psi :: g \Rightarrow h: A \to B \In \cat{K}\\ \quad \sigma :: v \Rightarrow w: B \to C \In \cat{K}\\ \quad \tau :: v \Rightarrow w: B \to C \In \cat{K}$

$\&$ -推論規則を恒等射の記号を使って書けば：

$\quad (\alpha \,\overset{\id}{\equiv\!\gt}\, \beta) \& (\beta \,\overset{\id}{\equiv\!\gt}\, \gamma) \overset{\id}{\to^4} (\alpha \,\overset{\id}{\equiv\!\gt}\, \gamma)$

3-射 $(\alpha \,\overset{\id}{\equiv\!\gt}\, \beta)$ と $(\beta \,\overset{\id}{\equiv\!\gt}\, \gamma)$ を $\&$ -結合（(3, 2)-結合）した結果は $(\alpha \,\overset{\id}{\equiv\!\gt}\, \gamma)$ に等しいことを主張しています。「3-射が等しい」の等しさは4-射なので $\overset{\id}{\to^4}$ で書いています。つまり、 $\&$ -推論規則の圏論的対応物は3-射への演算と等式である恒等4-射だと言えます。

$;$ -推論規則を恒等射の記号を使って書けば：

$\quad (\alpha \,\overset{\id}{\equiv\!\gt}\, \beta); (\phi \,\overset{\id}{\equiv\!\gt}\, \psi) \overset{\id}{\to^4} ( \alpha;\phi \,\overset{\id}{\equiv\!\gt}\, \beta; \psi)$

3-射の $;$ -結合（(3, 1)-結合）に関する等式（恒等4-射）ですが、2-射の $;$ -結合（(2, 1)-結合、縦結合）に関する主張になっています。

$*$ -推論規則を恒等射の記号を使って書けば：

$\quad (\alpha \,\overset{\id}{\equiv\!\gt}\, \beta) *(\sigma \,\overset{\id}{\equiv\!\gt}\, \tau) \overset{\id}{\to^4} ( \alpha*\sigma \,\overset{\id}{\equiv\!\gt}\, \beta * \tau)$