このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

絵算で見る、拡張スタイルのモナドとモノイド・スタイルのモナド

雑記／備忘

「Haskellの二重コロン「::」とバインド記号「>>=」の説明」で、拡張スタイルのモナドとモノイド・スタイルのモナドの話題が出ました。この話題はだいぶ昔に書いたことがありますが、絵算の応用として「拡張スタイル ←→ モノイド・スタイル」の相互変換をしてみます。

内容：

絵算の技法

モナドの二種類の定義を行ったり来たりする、つまり「拡張スタイルのモナド ←→ モノイド・スタイルのモナド」の相互変換をするために、次の技法を使いましょう。

  1. 圏の圏における絵算〈{graphical | pictorial | diagrammatic} {calculation | computation}〉
  2. 図式順記法〈diagrammatic order notation〉
  3. 射の格上げ〈bump up | promotion〉
  4. オペレーターボックス〈operator box〉

これらの技法を使う実例としてモナドの定義を扱う、と言ったほうがいいかも知れません。この記事は絵算の練習問題と捉えましょう。

絵算、図式順記法、格上げについては、次の記事と、そこから参照されている記事を見てください。

オペレーターボックスは、関手ボックスを、関手とは限らないオペレーター〈コンビネータ〉にまで拡大して利用する手法です。アイディアは関手ボックスと同じです。関手ボックスについては、「絵算のススメ 2015 年末版 // 絵算のテクニック もっと：等号ノード、関手ボックス」で触れています（触れてるだけだな）。ストライプ図は関手ボックスの変種です -- 「モノイド関手／ラックス・モノイド関手とその実例 // マッカーディのストライプ図」に説明があります。

射のプロファイルとin記法もよく使うので、必要があれば次も参照してください。

モノイド・スタイルのモナドの定義

テキスト記法は図式順記法を使うので、必要があれば演算子記号の一覧表を確認してください。

モノイド・スタイルのモナドを (F, μ, η)/C と書いたとき、基礎となる圏Cと3つの構成素は（必ずしも小さくない）圏の圏CAT内で次のプロファイルを持ちます。

  1. C in CAT （基礎圏）
  2. F:C → C in CAT （台関手）
  3. μ::F＊F ⇒ F:C → C in CAT （乗法）
  4. η::C^ ⇒ F:C → C in CAT （単位）（C^ は IdC と同じ）

モノイド・スタイルのモナド法則は次の等式で書けます。

  1. assoc ::: μ＊F^ ; μ = F^＊μ ; μ :: F＊F＊F ⇒ F : C → C in CAT （結合律）
  2. lunit ::: η＊F^ ; μ = F :: C^＊F ⇒ F : C → C in CAT （左単位律）
  3. runit ::: F^＊η ; μ = F :: F＊C^ ⇒ F : C → C in CAT （右単位律）

左単位律、右単位律における左右の別は書き方・描き方に依存するので左右に絶対的意味はありません。

CATは2-圏〈厳密2-圏〉ですが、等式は2-圏の3-射です*1。次のように書いたほうが3-射であることが伝わるでしょう。

  • assoc ::: μ＊F^ ; μ ≡> F^＊μ ; μ :: F＊F＊F ⇒ F : C → C in CAT

等式＝3-射は、ストリング図の変形として表現されます。モナド法則（結合律と2つの単位律）がどのような変形かは後で出てくるので、絵は省略します。

拡張スタイルのモナドの定義

拡張スタイルのモナドを (T, η, (-)#)/C とします。Cは圏ですが、Tは関手ではないし、ηの自然性も仮定せず、(-)# は関手でも自然変換でもないオペレーターです。(-)# をExtとも書くことにします。T, η, Ext は、次のような形で定義します。

  1. For A∈|C|, T(A) in C （対象構成子*2）
  2. For A∈|C|, ηA:A → T(A) in C （単位）
  3. For A, B∈|C|, ExtA,B:C(A, T(B)) → C(T(A), T(B)) in Set （拡張オペレーター）

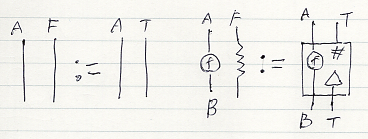
次の方針で図示します。描画方向は、縦結合が上から下、横結合が左から右です。

  1. T(A) を図式順で A.T と書いて、A T の順で横に並んだ2本のワイヤーにする。
  2. ηA を図式順で A.ηと書いて、A η の順で横に並んだワイヤーとノードにする。ηのノード形状は三角（'△'）にする。
  3. f;A → T(B) に対する f# = ExtA,B(f) は、fを表すノード＆ワイヤーを囲むボックスで描く。

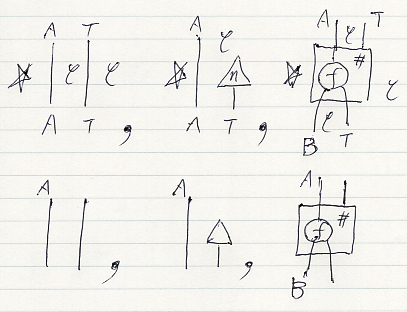
上段の絵では、エリア、ワイヤー、ノードにすべてラベルを付けています。

  1. エリア☆は、自明圏（単一対象と恒等射だけの圏）
  2. エリアCは、基礎圏
  3. ワイヤーAは、Cの対象の格上げ
  4. ワイヤーTは、対象構成子〈型構成子〉（関手ではないが、関手の対象パートになる）
  5. ノードηは、左に対象（の格上げ）があると射（の格上げ）になる射の族
  6. ノードfは、Cの射 f:A → B in C の格上げ
  7. 箱は、Extを表すオペレーターボックス

下段の絵では、ラベルがほぼ省略されています。実際の計算では、この程度の省略が行われます。

注意すべきは、この描画法は「正面からではなくて横から見て描いている」ことです。横が何を意味するかというと、「絵算をはじめた人への注意 // 3次元ビュー」のBさんからの視点です。通常の関手ボックスやストライプ図は正面（Aさん）から見ての絵です。

さて、拡張スタイルのモナド法則は次の等式で書けます。A, B, C は基礎圏Cの対象で、図式順記法を使います。

  1. A.η ; (f:A → B.T)# = (f:A → B.T)
  2. (A.η:A → A.T)# = (A.T)^ （(A.T)^ は idA.T と同じ）
  3. [(f:A → B.T);(g:B → C.T)#]# = (f:A → B.T)#;(g:B → C.T)#

それぞれの等式は次のように図示されます。格上げを使って、絵はCAT内で解釈します。

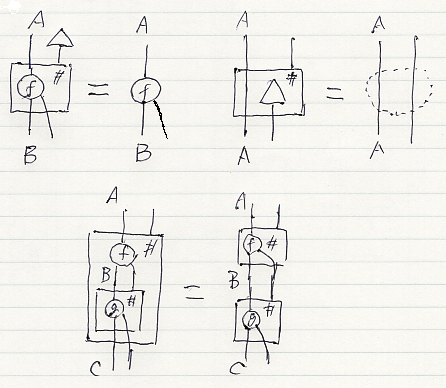
絵の印象から、3つの等式をそれぞれ、

  1. 外単位律〈outer unit law〉
  2. 内単位律〈inner unit law〉
  3. 入れ子律〈nest law〉

と呼ぶことにします。

  1. ボックスの右上に接合された単位（△）はボックスごと消せる。
  2. ボックスに入れられた単位（△）はボックスごと消せる。
  3. ボックスの入れ子を、並んだ2個のボックスに変形できる。

逆向きの変形もできます。

モノイド・スタイルから拡張スタイルへ

モノイド・スタイルのモナド (F, μ, η)/C の構成素は次の方針で図示します。

  1. F:C → C はワイヤーで描く。
  2. μ::F＊F ⇒ F は黒丸（●）で描く。
  3. η::C^ ⇒ F は三角（△）で描く。

与えられたモノイド・スタイルのモナド (F, μ, η)/C から、拡張スタイルのモナド (T, η, (-)#)/C を構成するには、次のように定義します。

  1. A.T := A.F
  2. A.η := A.η
  3. (f:A → B.T)# := (f:A → B.T).F ; B.μ

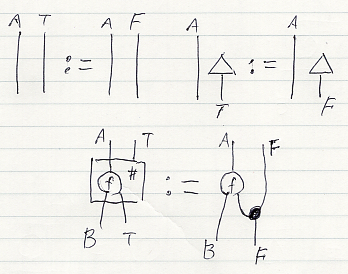
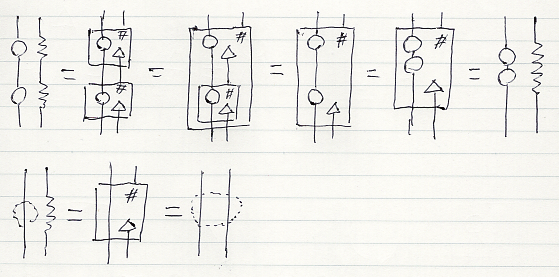
この定義のもとで、拡張スタイルのモナド法則（外単位律、内単位律、入れ子律）を示せばいいのですが、図の変形として比較的容易に示せます。

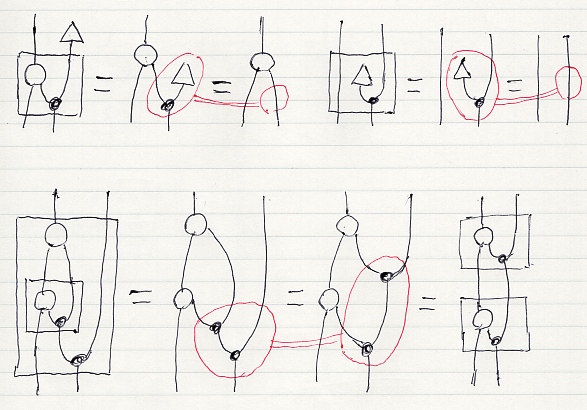
赤で描いているのは、モノイド・スタイルのモナドの右単位律、左単位律、結合律による変形です。（結合律による変形に、交替律によるノードの移動も混じってしまってますね。絵算あるある*3。）

拡張スタイルからモノイド・スタイルへ 素材の準備

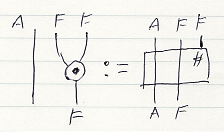
与えられた拡張スタイルのモナド (T, η, (-)#)/C から、モノイド・スタイルのモナド (F, μ, η)/C を構成するには、まずFを次のように定義します。

  • A.F := A.T （Fの対象パート）
  • (f:A → B).F := [(f:A → B) ; B.η]# （Fの射パート）

Fの射パートは、実線のワイヤーではなくて波線（グニグニ）にします*4。対象パートは F = T なので実線のままです。

定義したFが関手であることは証明する必要があります。関手性は次のとおりです。

  • (f;g).F = f.F ; g.F （結合の保存）
  • A^.F = (A.F)^ （恒等射の保存）

絵算で示しましょう。

絵の変形に使っているのは、F（波線）の定義、入れ子律、外単位律、内単位律です。

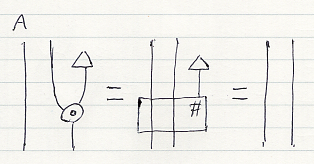
ηはそのまま使いますが、拡張スタイルのηでは自然性を仮定してなかったので、自然性の証明が必要です。（下の図式で、あえて対象にはT、射にはFを使っています。）

\require{AMScd} \begin{CD} A @>{A.\eta}>> A.T \\ @V{f}VV @VV{f.F}V \\ B @>{B.\eta}>> B.T \end{CD}\\ \mbox{commutative in }\mathcal{C}

ストリング図における自然性は、エレベータ法則になります。以下のように示せます。

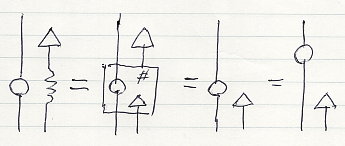
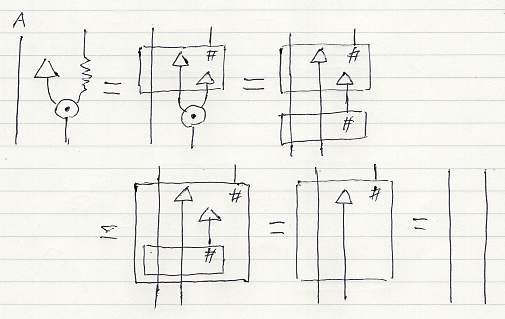
モノイド・スタイルのモナド乗法μは次のように定義します。

  • A.μ := [(A.T)^]# （対象に対しては T = F）

「定義されたモナド乗法」であることを強調するために、二重丸にしました。

μの自然性も証明が必要です。

\begin{CD} A.(T\ast T) @>{A.\mu}>> A.T \\ @V{f.(F\ast F)}VV @VV{f.F}V \\ B.(T\ast T) @>{B.\mu}>> B.T \end{CD}\\ \mbox{commutative in }\mathcal{C}

絵算でエレベータ法則を示します。使うのは（当然ながら）、μの定義、F（射パート）の定義、拡張スタイルのモナド法則だけです。

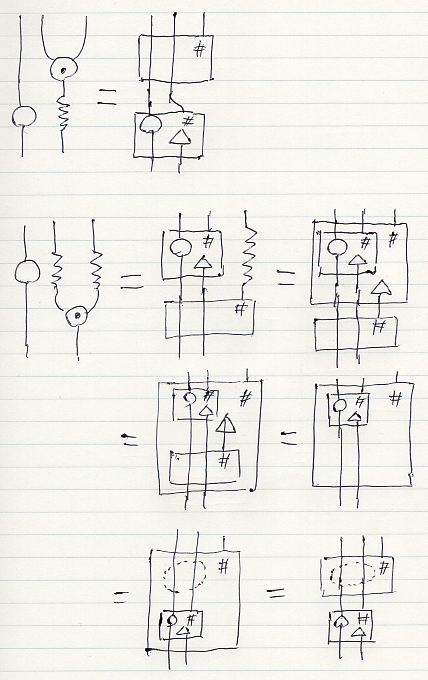
拡張スタイルからモノイド・スタイルへ 法則の証明

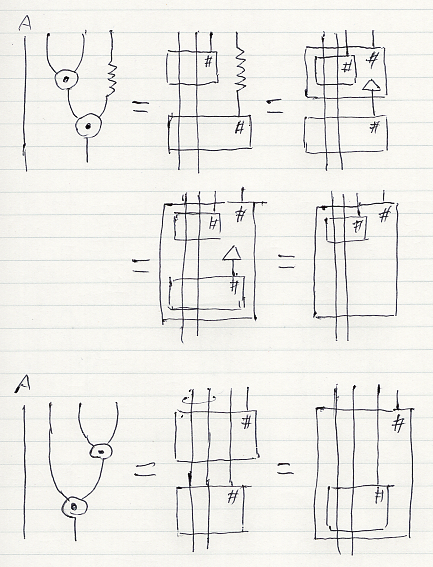
拡張スタイルのモナド (T, η, (-)#)/C から構成された F, μ, η からなるモノイド・スタイルのモナド (F, μ, η)/C が、結合法則、右単位律、左単位律を満たすことを示す必要があります。それを示せれば、構成された (F, μ, η)/C は間違いなくモノイド・スタイルのモナドになります。

モノイド・スタイルのモナド法則は次のように示せます。煩雑になるので（それとめんどうなので）、ラベルは省略してますが、ラベルを補って解読してみてください。



おわりに

モノイド・スタイルはモノイドと同様に扱えるので、モナドの代数的な扱いには有利です。拡張スタイルはプログラミングではよく使われているし、モナド法則の証明がモノイド・スタイルより容易になる場合があります。それぞれ一長一短があるので、どちらか一方だけというわけにはいきません。

モノイド・スタイルと拡張スタイルは、可逆な翻訳で行き来できるという意味で同値です。この記事で、その同値性が成立することを実際に確認しました*5。細部まで観測することにより、両方のスタイルの定義が非常に巧みにできてるなーと感得できたのではないでしょうか。

*1:2-圏にも3次元以上の射が存在します。ただし、3次元以上には自明な射＝恒等射しかありません。

*2:プログラミングでは型構成子ですが、型を圏論の言葉で言えば対象です。

*3:交替律によるノードの移動は、無意識にできる（やってしまう）ので、テキスト計算だと2ステップ・3ステップを一度にやってしまうことが多いのです。

*4:以前、口頭で「絵算使えば簡単」とか言って計算し始めてうまくいかなかった事があります。グニグニを使わなかったせいだと思います。

*5:実は、行って返ってきたら元と同じである証明が欠けてますが、補ってくださいませ。