昨日の記事「アイレンベルグ/ムーア圏 その3:Maybeモナドのとき」の注釈に次のように書きました。
型パラメータを明示的に書くプログラミング言語風の記法が、圏論の記述には向いてないのかも知れません。圏論に最適化された記法や絵図を使うと、もっと単純な記述ができます。
「圏論に最適化された記法や絵図」とはなんでしょうか。まず、絵図(picture, diagram)としては、グロービュラー図(globular diagram)とストリング図(string diagram)が典型的です。1次元のときのグロービュラー図*1は、通常のドット&アロー図となります。ストリング図は、グロービュラー図のポアンカレ双対となります。ストリング図のほうが図形的直感*2が効くので、実際の計算にはストリング図が便利でしょう。
高次圏(n-圏)では、絵図は「便利な表現法」ではなくて、定義の一部になります。そのへんの事は以前少し書いたことがあります。
今日は絵図の話ではなくて、テキスト記法について少し述べます。
内容
反図式順記法と図式順記法
テキストで書かれる普通の数学的記法、あるいはテキストで書かれるプログラミング言語風の記法は、圏論の記述や計算にはあんまり向かないのじゃないか、と僕は思っています。
「fの後にgを結合する」を、gf と書くことがあるのですが、これが図式の方向とも時間的順序とも逆ですごくイヤ。やはり、f;g がイイです。f;g のスタイルは図式順(diagrammatic order)記法といいます。もっとも、バックハウス(Roland Backhouse)、ウィラートン (Simon Willerton) 、ツビタノビッチ(Predrag Cvitanovic)などは、矢印を g:C←B, f:B←A と書いて、g
f に合わせようとしてますがね。
図式順を採用してもストレスがたまるのは、(f;g)(x) = g(f(x)) のようなときに、結局は反図式順が混じってしまい、バイダイレクショナルな行ったり来たりが発生することです。この「行ったり来たり」が積み重なると、すごく負担になります。左右の区別が苦手な僕にはもう耐え難い。
そこで、反図式順をまったく含まない記法として、図式順テキスト記法というのをだいぶ前から使っています。これは僕(檜山)のローカル記法なんで表立っては使いませんが、自分で計算するときはコレでやっています。ストレスは少ないです。「テキスト記法」と呼んでいるのは、ギリシャ文字は例外としてアスキーの範囲内の記号だけを使うからです。
図式順テキスト記法
図式順テキスト記法を系統的に説明することはしませんが、その特徴と注意点をバラバラと挙げます。
- 圏の対象は、大文字A, Bではなくて小文字a, bで表します。
- 圏の対象と射は英字小文字、圏と関手は英字大文字、自然変換はギリシャ文字小文字と決め打ちなので一目瞭然。
- 複数文字からなる語は使わず、一文字を使います。ただし、f, f', f'' などのプライム(ダッシュ)は許します。
- f(x) のように、丸括弧を適用に使うことは絶対にしません。f(x) は xf と書きます(後述)。
- 射の結合(合成)、関手の結合、自然変換の横結合(スター席)は標準的な演算と考えて、演算記号を省略することがあります。
- 上記以外の演算記号は省略しません!
要素や関数適用は存在しない
圏の対象は集合ではない(一般的には、集合だと仮定してはいけない)ので、「対象の要素」という概念はありません。圏の射は関数ではない(一般的には、関数だと仮定してはいけない)ので、関数に引数を渡す「適用」もありません。ですから、x∈A に対する f(x) という記法は出て来ません。不要だし無意味です。
とはいっても、「要素と適用が欲しい」と思う人は多いでしょう。ご安心ください; f(x) を xf と書けばいいだけです。以下に説明しましょう。
圏Cに終対象とかモノイド単位があるとして、それを 1 と書きます。aが圏の対象だとして、x:1→a をaの要素のごとく扱います。f:a→b があれば、xとfはこの順で結合できるので、x;f が意味を持ちます。射の結合を表す「;」を省略することは許すので、x;f = xf と書いてもいいわけです。対応をまとめておくと次のとおり。
| 集合の概念 | 圏の概念 |
|---|---|
| 集合A | 対象a |
| x∈A | x:1→a |
| 関数 f:A→B | 射f:a→b |
| 適用した値 f(x) | 結合 xf |
(f;g)(x) = g(f(x)) は、x(fg) = (xf)g と、単なる結合律として書けます。
自然変換の計算
F:C→D が関手のとき、Fによる対象aの値は a.F と書きます。これは aF とは書きません。f:a→b を関手Fで写すと f.F:a.F→b.F となります。F:C→D、G:D→E の結合は、F;G です*3が、FG と書いてもいいので、a.(FG) = (a.F).G が成立します。ドット(.)は左結合的とすれば、(a.F).G は a.F.G と書けます。
αが自然変換 α::F⇒G:C→D のとき、αa は a.α と書きます。こうすれば、面倒な下付き添字を使わずに書けます。関手のときと同じ記法で問題ないのか?と言うとヘイキです。むしろ、どちらもドットを使うと具合がいいのです。
α::F⇒G:C→D、β::G→D:C→D のとき、αとβの縦結合(垂直結合)は、α|β と書きます。このときのパイプ記号は省略できません。自然変換は成分射を与えれば決まるので、α|β は次のように定義されていると思ってかまいません。
- a.(α|β) := (a.α);(a.β)
ドットがセミコロンより優先度が高いと約束すれば、(a.α);(a.β) は a.α;a.β と書けます。
α::F⇒G:C→D、β::H→K:D→E のとき、αとβの横結合(水平結合)は、α;β または αβ と書きます。α*β と書くこともあります -- これは、横結合をスター積と呼ぶ習慣があるからです。縦結合のほうを αβ と書く流儀もありますが、縦結合と横結合を混同するのは極めてマズイので、縦結合のほうは必ずパイプ記号を付けることにします。
自然変換の計算では、関手と自然変換の横結合がよく出てきます。α::F⇒G:C→D、H:D→E のとき αH::FH⇒GH:C→E は次のように定義されます。
- a.(αH) := a.α.H
見た目が非常にシンプルです。
F:C→D、β::H⇒K:D→E のときは、
- a.(Fβ) = a.F.β
まったく同じ形で書けます。
α::F⇒G:C→D、β::H⇒K:D→E に対する αβ の定義と計算には、次の交替律を使います。
- αH|Gβ = Fβ|αH = αβ
つまり、αβは αH|Gβ または Fβ|αH を使って計算できます。
- a.(αβ) = a.(αH|Gβ) = a.(αH);a.(Gβ) = (a.α.H);(a.G.β)
- a.(αβ) = a.(Fβ|αH) = a.(Fβ);a.(αH) = (a.F.β);(a.α.H)
通常の記法に比べるとずっと単純だと思いますが、いかがでしょう。
メモ編に横結合の説明図があったので引用します*4。この図では、圏の対象が大文字で、その他使っている文字が「α::F⇒F':C→D, β::G⇒G':D→E の横結合 α*β::F;G⇒F';G':C→E」となっています。
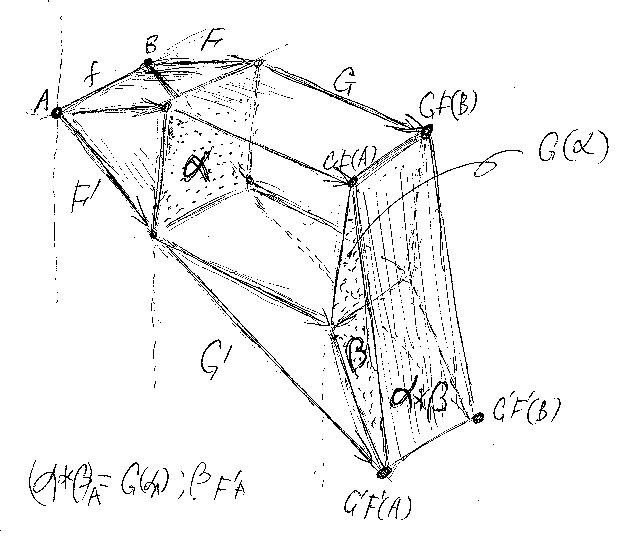
図中に通常の記法で (α*β)A = G(αA);βF'(A) と書いていますが、大文字Aを小文字aに直すと、これは次のように書けます。
- a.(α*β) = (a.α.G);(a.F'.β)
さらに、F' → G, G → H と置き換えれば、a.(αβ) = (a.α.H);(a.G.β) となり、先の定義とまったく同じです。